Recurrence plot
Encyclopedia
In descriptive statistics
and chaos theory
, a recurrence plot (RP) is a plot showing, for a given moment in time, the times at which a phase space
trajectory visits roughly the same area in the phase space
. In other words, it is a graph of
showing
on a horizontal axis and 
on a vertical axis, where 
is a phase space
trajectory.
, is a fundamental property of deterministic dynamical systems and is typical for nonlinear or chaotic systems (cf. Poincaré recurrence theorem
). The recurrence of states in nature has been known for a long time and has also been discussed in early work (e.g. Henri Poincaré
1890).
. Usually, a phase space does not have a low enough dimension (two or three) to be pictured. Higher-dimensional phase spaces can only be visualized by projection into the two or three-dimensional sub-spaces. However, Eckmann's tool enables us to investigate the m-dimensional phase space trajectory through a two-dimensional representation of its recurrences. Such recurrence of a state at time i and a different time j is pictured within a two-dimensional squared matrix with black and white dots, where black dots mark a recurrence, and both axes are time axes. This representation is called recurrence plot. Such a recurrence plot can be mathematically expressed as
where N is the number of considered states
, ε is a threshold distance, || · || a norm (e.g. Euclidean norm) and H the Heaviside step function
. If only a time series
is available, the phase space can be reconstructed by using a time delay embedding (see Takens' theorem
):
where u(i) is the time series, m the embedding dimension and
the time delay.
Caused by characteristic behaviour of the phase space trajectory, a recurrence plot contains typical small-scale structures, as single dots, diagonal lines and vertical/horizontal lines (or a mixture of the latter, which combines to extended clusters). The large-scale structure, also called texture, can be visually characterised by homogenous, periodic, drift or disrupted. The visual appearance of an RP gives hints about the dynamics of the system.
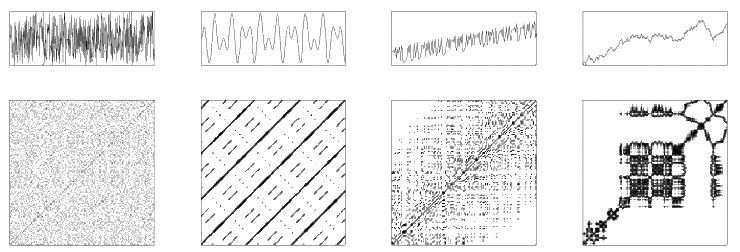The small-scale structures in RPs are used by the recurrence quantification analysis
(Zbilut & Webber 1992; Marwan et al. 2002). This quantification allows to describe the RPs in a quantitative way, and to study transitions or nonlinear parameters of the system. In contrast to the heuristic approach of the recurrence quantification analysis, which depends on the choice of the embedding parameters, some dynamical invariants as correlation dimension
, K2 entropy or mutual information
, which are independent on the embedding, can also be derived from recurrence plots. The base for these dynamical invariants are the recurrence rate and the distribution of the lengths of the diagonal lines.
Close returns plots are similar to recurrence plots. The difference is that the relative time between recurrences is used for the
-axis (instead of absolute time).
The main advantage of recurrence plots is that they provide useful information even for short and non-stationary data, where other methods fail.
Cross recurrence plots consider the phase space trajectories of two different systems in the same phase space (Marwan & Kurths 2002):
The dimension of both systems must be the same, but the number of considered states (i.e. data length) can be different. Cross recurrence plots compare the simultaneous occurrences of similar states of two systems. They can be used in order to analyse the similarity of the dynamical evolution between two different systems, to look for similar matching patterns in two systems, or to study the time-relationship of two similar systems, whose time-scale differ (Marwan & Kurths 2005).
Joint recurrence plots are the Hadamard product of the recurrence plots of the considered sub-systems (Romano et al. 2004), e.g. for two systems
and 
the joint recurrence plot is
In contrast to cross recurrence plots, joint recurrence plots compare the simultaneous occurrence of recurrences in two (or more) systems. Moreover, the dimension of the considered phase spaces can be different, but the number of the considered states has to be the same for all the sub-systems. Joint recurrence plots can be used in order to detect phase synchronisation
.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
and chaos theory
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
, a recurrence plot (RP) is a plot showing, for a given moment in time, the times at which a phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
trajectory visits roughly the same area in the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
. In other words, it is a graph of
showing
on a horizontal axis and on a vertical axis, where is a phase spacePhase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
trajectory.
Background
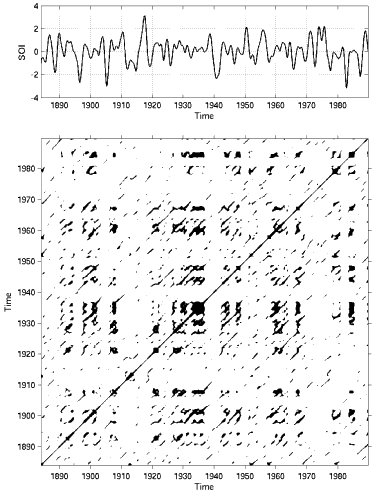
Natural processes can have a distinct recurrent behaviour, e.g. periodicities (as seasonal or Milankovich cycles), but also irregular cyclicities (as El Niño Southern Oscillation). Moreover, the recurrence of states, in the meaning that states are again arbitrarily close after some time of divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, is a fundamental property of deterministic dynamical systems and is typical for nonlinear or chaotic systems (cf. Poincaré recurrence theorem
Poincaré recurrence theorem
In mathematics, the Poincaré recurrence theorem states that certain systems will, after a sufficiently long time, return to a state very close to the initial state. The Poincaré recurrence time is the length of time elapsed until the recurrence. The result applies to physical systems in which...
). The recurrence of states in nature has been known for a long time and has also been discussed in early work (e.g. Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
1890).
Detailed description
Eckmann et al. (1987) introduced recurrence plots, which can visualize the recurrence of states in a phase spacePhase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
. Usually, a phase space does not have a low enough dimension (two or three) to be pictured. Higher-dimensional phase spaces can only be visualized by projection into the two or three-dimensional sub-spaces. However, Eckmann's tool enables us to investigate the m-dimensional phase space trajectory through a two-dimensional representation of its recurrences. Such recurrence of a state at time i and a different time j is pictured within a two-dimensional squared matrix with black and white dots, where black dots mark a recurrence, and both axes are time axes. This representation is called recurrence plot. Such a recurrence plot can be mathematically expressed as
where N is the number of considered states
, ε is a threshold distance, || · || a norm (e.g. Euclidean norm) and H the Heaviside step functionHeaviside step function
The Heaviside step function, or the unit step function, usually denoted by H , is a discontinuous function whose value is zero for negative argument and one for positive argument....
. If only a time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
is available, the phase space can be reconstructed by using a time delay embedding (see Takens' theorem
Takens' theorem
In mathematics, a delay embedding theorem gives the conditions under which a chaotic dynamical system can be reconstructed from a sequence of observations of the state of a dynamical system...
):
where u(i) is the time series, m the embedding dimension and
the time delay.Caused by characteristic behaviour of the phase space trajectory, a recurrence plot contains typical small-scale structures, as single dots, diagonal lines and vertical/horizontal lines (or a mixture of the latter, which combines to extended clusters). The large-scale structure, also called texture, can be visually characterised by homogenous, periodic, drift or disrupted. The visual appearance of an RP gives hints about the dynamics of the system.
Recurrence quantification analysis
Recurrence quantification analysis is a method of nonlinear data analysis for the investigation of dynamical systems. It quantifies the number and duration of recurrences of a dynamical system presented by its phase space trajectory....
(Zbilut & Webber 1992; Marwan et al. 2002). This quantification allows to describe the RPs in a quantitative way, and to study transitions or nonlinear parameters of the system. In contrast to the heuristic approach of the recurrence quantification analysis, which depends on the choice of the embedding parameters, some dynamical invariants as correlation dimension
Correlation dimension
In chaos theory, the correlation dimension is a measure of the dimensionality of the space occupied by a set of random points, often referred to as a type of fractal dimension....
, K2 entropy or mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
, which are independent on the embedding, can also be derived from recurrence plots. The base for these dynamical invariants are the recurrence rate and the distribution of the lengths of the diagonal lines.
Close returns plots are similar to recurrence plots. The difference is that the relative time between recurrences is used for the
-axis (instead of absolute time).The main advantage of recurrence plots is that they provide useful information even for short and non-stationary data, where other methods fail.
Extensions
Multivariate extensions of recurrence plots were developed as cross recurrence plots and joint recurrence plots.Cross recurrence plots consider the phase space trajectories of two different systems in the same phase space (Marwan & Kurths 2002):
The dimension of both systems must be the same, but the number of considered states (i.e. data length) can be different. Cross recurrence plots compare the simultaneous occurrences of similar states of two systems. They can be used in order to analyse the similarity of the dynamical evolution between two different systems, to look for similar matching patterns in two systems, or to study the time-relationship of two similar systems, whose time-scale differ (Marwan & Kurths 2005).
Joint recurrence plots are the Hadamard product of the recurrence plots of the considered sub-systems (Romano et al. 2004), e.g. for two systems
and the joint recurrence plot isIn contrast to cross recurrence plots, joint recurrence plots compare the simultaneous occurrence of recurrences in two (or more) systems. Moreover, the dimension of the considered phase spaces can be different, but the number of the considered states has to be the same for all the sub-systems. Joint recurrence plots can be used in order to detect phase synchronisation
Phase synchronization
Phase synchronization is the process by which two or more cyclic signals tend to oscillate with a repeating sequence of relative phase angles.Phase synchronisation is usually applied to two waveforms of the same frequency with identical phase angles with each cycle...
.
Example
See also
- Recurrence quantification analysisRecurrence quantification analysisRecurrence quantification analysis is a method of nonlinear data analysis for the investigation of dynamical systems. It quantifies the number and duration of recurrences of a dynamical system presented by its phase space trajectory....
, a heuristic approach to quantify recurrence plots. - Recurrence period density entropyRecurrence period density entropyRecurrence period density entropy is a method, in the fields of dynamical systems, stochastic processes, and time series analysis, for determining the periodicity, or repetitiveness of a signal.- Overview :...
, an information-theoretic method for summarising the recurrence properties of both deterministic and stochastic dynamical systems. - Self-similarity matrixSelf-similarity matrixIn data analysis, the self-similarity matrix is a graphical representation of similar sequences in a data series. Similarity can be explained by different measures, like spatial distance , correlation, or comparison of local histograms or spectral properties...
- Poincaré plotPoincaré plotA Poincaré plot, named after Henri Poincaré, is used to quantify self-similarity in processes, usually periodic functions. It is also known as a return map.Given a time series of the form...