Recurrence period density entropy
Encyclopedia
Recurrence period density entropy (RPDE) is a method, in the fields of dynamical systems, stochastic processes, and time series analysis, for determining the periodicity, or repetitiveness of a signal.
and time delayed mutual information, except that it measures repetitiveness in the phase space
of the system, and is thus a more reliable measure based upon the dynamics of the underlying system that generated the signal. It has the advantage that it does not require the assumptions of linearity, Gaussianity or dynamical determinism. It has been successfully used to detect abnormalities in biomedical contexts such as speech signal.
The RPDE value
is a scalar in the range zero to one. For purely periodic signals, 
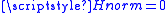, whereas for purely i.i.d., uniform white noise
,
.
of a time series in phase space
, which, according to stochastic extensions to Taken's embedding theorems, can be carried out by forming time-delayed vectors:
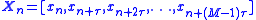
for each value xn in the time series, where M is the embedding dimension, and τ is the embedding delay. These parameters are obtained by systematic search for the optimal set (due to lack of practical embedding parameter techniques for stochastic systems) (Stark et al. 2003). Next, around each point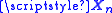
in the phase space, an 
-neighbourhood (an m-dimensional ball with this radius) is formed, and every time the time series returns to this ball, after having left it, the time difference T between successive returns is recorded in a histogram
. This histogram is normalised to sum to unity, to form an estimate of the recurrence period density function P(T). The normalised entropy
of this density:
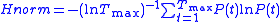
is the RPDE value, where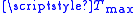
is the largest recurrence value (typically on the order of 1000 samples). Note that RPDE is intended to be applied to both deterministic and stochastic signals, therefore, strictly speaking, Taken's original embedding theorem does not apply, and needs some modification.
or linear prediction
. The recurrence period density is a sparse representation for nonlinear, non-Gaussian and nondeterministic signals, whereas the Fourier transform
is only sparse for purely periodic signals.
Overview
Recurrence period density entropy is useful for characterising the extent to which a time series repeats the same sequence, and is therefore similar to linear autocorrelationAutocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
and time delayed mutual information, except that it measures repetitiveness in the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
of the system, and is thus a more reliable measure based upon the dynamics of the underlying system that generated the signal. It has the advantage that it does not require the assumptions of linearity, Gaussianity or dynamical determinism. It has been successfully used to detect abnormalities in biomedical contexts such as speech signal.
The RPDE value
is a scalar in the range zero to one. For purely periodic signals, 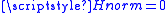, whereas for purely i.i.d., uniform white noiseWhite noise
White noise is a random signal with a flat power spectral density. In other words, the signal contains equal power within a fixed bandwidth at any center frequency...
,
.Method description
The RPDE method first requires the embeddingEmbedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of a time series in phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
, which, according to stochastic extensions to Taken's embedding theorems, can be carried out by forming time-delayed vectors:
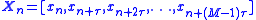
for each value xn in the time series, where M is the embedding dimension, and τ is the embedding delay. These parameters are obtained by systematic search for the optimal set (due to lack of practical embedding parameter techniques for stochastic systems) (Stark et al. 2003). Next, around each point
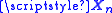in the phase space, an -neighbourhood (an m-dimensional ball with this radius) is formed, and every time the time series returns to this ball, after having left it, the time difference T between successive returns is recorded in a histogramHistogram
In statistics, a histogram is a graphical representation showing a visual impression of the distribution of data. It is an estimate of the probability distribution of a continuous variable and was first introduced by Karl Pearson...
. This histogram is normalised to sum to unity, to form an estimate of the recurrence period density function P(T). The normalised entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of this density:
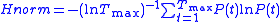
is the RPDE value, where
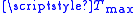is the largest recurrence value (typically on the order of 1000 samples). Note that RPDE is intended to be applied to both deterministic and stochastic signals, therefore, strictly speaking, Taken's original embedding theorem does not apply, and needs some modification.RPDE in practice
RPDE has the ability to detect subtle changes in natural biological time series such as the breakdown of regular periodic oscillation in abnormal cardiac function which are hard to detect using classical signal processing tools such as the Fourier transformFourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
or linear prediction
Linear prediction
Linear prediction is a mathematical operation where future values of a discrete-time signal are estimated as a linear function of previous samples....
. The recurrence period density is a sparse representation for nonlinear, non-Gaussian and nondeterministic signals, whereas the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
is only sparse for purely periodic signals.
See also
- Recurrence plotRecurrence plotIn descriptive statistics and chaos theory, a recurrence plot is a plot showing, for a given moment in time, the times at which a phase space trajectory visits roughly the same area in the phase space...
, a powerful visualisation tool of recurrences in dynamical (and other) systems. - Recurrence quantification analysisRecurrence quantification analysisRecurrence quantification analysis is a method of nonlinear data analysis for the investigation of dynamical systems. It quantifies the number and duration of recurrences of a dynamical system presented by its phase space trajectory....
, another approach to quantify recurrence properties.
External links
- Fast MATLAB code for calculating the RPDE value.
- http://www.recurrence-plot.tk/