
Toeplitz algebra
Encyclopedia
In operator algebras, the Toeplitz algebra is the C*-algebra generated by the unilateral shift on the Hilbert space
l2(N)
. Taking l2(N) to be the Hardy space
H2
, the Toeplitz algebra consists of elements of the form
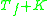
where Tf is a Toeplitz operator
with continuous symbol and K is a compact operator
.
Toeplitz operators with continuous symbols commute modulo the compact operators. So the Toeplitz algebra can be viewed as the C*-algebra extension of continuous functions on the circle by the compact operators. This extension is called the Toeplitz extension.
By Atkinson's theorem
, an element of the Toeplitz algebra Tf + K is a Fredholm operator
if and only if the symbol f of Tf is invertible. In that case, the Fredholm index of Tf + K is precisely the winding number
of f, the equivalence class of f in the fundamental group
of the circle. This is a special case of the Atiyah-Singer index theorem.
Wold decomposition
characterizes proper isometries
acting on a Hilbert space. From this, together with properties of Toeplitz operators, one can conclude that the Toeplitz algebra is the universal C*-algebra generated by a proper isometry; this is Coburn's theorem.
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
l2(N)
Sequence space
In functional analysis and related areas of mathematics, a sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K of real or complex numbers...
. Taking l2(N) to be the Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
H2
H square
In mathematics and control theory, H2, or H-square is a Hardy space with square norm. It is a subspace of L2 space, and is thus a Hilbert space...
, the Toeplitz algebra consists of elements of the form
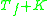
where Tf is a Toeplitz operator
Toeplitz operator
In operator theory, a Toeplitz operator is the compression of a multiplication operator on the circle to the Hardy space.- Details :Let S1 be the circle, with the standard Lebesgue measure, and L2 be the Hilbert space of square-integrable functions. A bounded measurable function g on S1 defines a...
with continuous symbol and K is a compact operator
Compact operator on Hilbert space
In functional analysis, compact operators on Hilbert spaces are a direct extension of matrices: in the Hilbert spaces, they are precisely the closure of finite-rank operators in the uniform operator topology. As such, results from matrix theory can sometimes be extended to compact operators using...
.
Toeplitz operators with continuous symbols commute modulo the compact operators. So the Toeplitz algebra can be viewed as the C*-algebra extension of continuous functions on the circle by the compact operators. This extension is called the Toeplitz extension.
By Atkinson's theorem
Atkinson's theorem
In operator theory, Atkinson's theorem gives a characterization of Fredholm operators.- The theorem :Let H be a Hilbert space and L the set of bounded operators on H...
, an element of the Toeplitz algebra Tf + K is a Fredholm operator
Fredholm operator
In mathematics, a Fredholm operator is an operator that arises in the Fredholm theory of integral equations. It is named in honour of Erik Ivar Fredholm....
if and only if the symbol f of Tf is invertible. In that case, the Fredholm index of Tf + K is precisely the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
of f, the equivalence class of f in the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the circle. This is a special case of the Atiyah-Singer index theorem.
Wold decomposition
Wold decomposition
In operator theory, the Wold decomposition, named after Herman Wold, or Wold-von Neumann decomposition, after Wold and John von Neumann, is a classification theorem for isometric linear operators on a given Hilbert space...
characterizes proper isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
acting on a Hilbert space. From this, together with properties of Toeplitz operators, one can conclude that the Toeplitz algebra is the universal C*-algebra generated by a proper isometry; this is Coburn's theorem.

