H square
Encyclopedia
In mathematics
and control theory
, H2, or H-square is a Hardy space
with square norm. It is a subspace of L2 space
, and is thus a Hilbert space
. In particular, it is a reproducing kernel Hilbert space
.
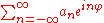
whereas elements of H2 are given by
The projection from L2 to H2 (by setting an = 0 when n < 0) is orthogonal.
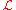given by
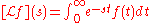
can be understood as a linear operator
where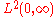
is the set of square-integrable functions on the positive real number line, and 
is the right half of the complex plane. It is more; it is an isomorphism
, in that it is invertible, and it isometric
, in that it satisfies
The Laplace transform is "half" of a Fourier transform; from the decomposition
one then obtains an orthogonal decomposition of
into two Hardy spaces
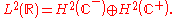
This is essentially the Paley-Wiener theorem.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
, H2, or H-square is a Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
with square norm. It is a subspace of L2 space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, and is thus a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. In particular, it is a reproducing kernel Hilbert space
Reproducing kernel Hilbert space
In functional analysis , a reproducing kernel Hilbert space is a Hilbert space of functions in which pointwise evaluation is a continuous linear functional. Equivalently, they are spaces that can be defined by reproducing kernels...
.
On the unit circle
In general, elements of L2 on the unit circle are given by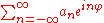whereas elements of H2 are given by
The projection from L2 to H2 (by setting an = 0 when n < 0) is orthogonal.
On the half-plane
The Laplace transform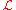 given bycan be understood as a linear operator
where
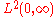is the set of square-integrable functions on the positive real number line, and is the right half of the complex plane. It is more; it is an isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, in that it is invertible, and it isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
, in that it satisfies
The Laplace transform is "half" of a Fourier transform; from the decomposition
one then obtains an orthogonal decomposition of
into two Hardy spaces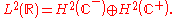This is essentially the Paley-Wiener theorem.