
Clifford's theorem
Encyclopedia
In mathematics
, Clifford's theorem on special divisors is a result of W. K. Clifford
on algebraic curve
s, showing the constraints on special linear systems on a curve C.
If D is a divisor on C, then D is (abstractly) a formal sum of points P on C (with integer coefficients), and in this application a set of constraints to be applied to functions on C (if C is a Riemann surface
, these are meromorphic function
s, and in general lie in the function field
of C). Functions in this sense have a divisor of zeros and poles, counted with multiplicity; a divisor D is here of interest as a set of constraints on functions, insisting that poles at given points are only as bad as the positive coefficients in D indicate, and that zeros at points in D with a negative coefficient have at least that multiplicity. The dimension of the vector space
of such functions is finite, and denoted ℓ(D). Conventionally the linear system of divisors
attached to D is then attributed dimension r(D) = ℓ(D) − 1, which is the dimension of the projective space
parametrizing it.
The other significant invariant of D is its degree, d, which is the sum of all its coefficients.
A divisor is called special
if ℓ(K − D) > 0, where K is the canonical divisor.
In this notation, Clifford's theorem is the statement that for a special divisor
D ≠ 0,
together with the information that the case of equality here is only for C a hyperelliptic curve, and D an integral multiple of the canonical divisor K.
The Clifford index of C is then defined as the minimum value of the d − 2r(D), taken over all special divisors. Clifford's theorem is then the statement that this is non-negative. The Clifford index for a generic curve of genus
g is known to be the floor function
of
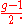
A conjecture of Michael Green states that the Clifford index for a curve over the complex numbers that is not hyperelliptic should be determined by the extent to which C as canonical curve has linear syzygies. In detail, the invariant a(C) is determined by the minimal free resolution of the homogeneous coordinate ring
of C in its canonical embedding, as the largest index i for which the graded Betti number βi, i + 2 is zero. Green and Lazarsfeld showed that a(C) + 1 is a lower bound for the Clifford index, and Green's conjecture is that equality always holds. There are numerous partial results.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Clifford's theorem on special divisors is a result of W. K. Clifford
William Kingdon Clifford
William Kingdon Clifford FRS was an English mathematician and philosopher. Building on the work of Hermann Grassmann, he introduced what is now termed geometric algebra, a special case of the Clifford algebra named in his honour, with interesting applications in contemporary mathematical physics...
on algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s, showing the constraints on special linear systems on a curve C.
If D is a divisor on C, then D is (abstractly) a formal sum of points P on C (with integer coefficients), and in this application a set of constraints to be applied to functions on C (if C is a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, these are meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s, and in general lie in the function field
Function field
Function field may refer to:*Function field of an algebraic variety*Function field...
of C). Functions in this sense have a divisor of zeros and poles, counted with multiplicity; a divisor D is here of interest as a set of constraints on functions, insisting that poles at given points are only as bad as the positive coefficients in D indicate, and that zeros at points in D with a negative coefficient have at least that multiplicity. The dimension of the vector space
- L(D)
of such functions is finite, and denoted ℓ(D). Conventionally the linear system of divisors
Linear system of divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family....
attached to D is then attributed dimension r(D) = ℓ(D) − 1, which is the dimension of the projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
parametrizing it.
The other significant invariant of D is its degree, d, which is the sum of all its coefficients.
A divisor is called special
Special divisor
In mathematics, in the theory of algebraic curves, certain divisors on a curve C are particular, in the sense of determining more compatible functions than would be predicted. These are the special divisors...
if ℓ(K − D) > 0, where K is the canonical divisor.
In this notation, Clifford's theorem is the statement that for a special divisor
Special divisor
In mathematics, in the theory of algebraic curves, certain divisors on a curve C are particular, in the sense of determining more compatible functions than would be predicted. These are the special divisors...
D ≠ 0,
- ℓ(D) − 1 ≤ d/2,
together with the information that the case of equality here is only for C a hyperelliptic curve, and D an integral multiple of the canonical divisor K.
The Clifford index of C is then defined as the minimum value of the d − 2r(D), taken over all special divisors. Clifford's theorem is then the statement that this is non-negative. The Clifford index for a generic curve of genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
g is known to be the floor function
Floor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
of
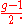
A conjecture of Michael Green states that the Clifford index for a curve over the complex numbers that is not hyperelliptic should be determined by the extent to which C as canonical curve has linear syzygies. In detail, the invariant a(C) is determined by the minimal free resolution of the homogeneous coordinate ring
Homogeneous coordinate ring
In algebraic geometry, the homogeneous coordinate ring R of an algebraic variety V given as a subvariety of projective space of a given dimension N is by definition the quotient ring...
of C in its canonical embedding, as the largest index i for which the graded Betti number βi, i + 2 is zero. Green and Lazarsfeld showed that a(C) + 1 is a lower bound for the Clifford index, and Green's conjecture is that equality always holds. There are numerous partial results.

