Clifford theory
Encyclopedia
In mathematics, Clifford theory, introduced by , describes the relation between representations of a group and those of a normal subgroup.
Alfred H. Clifford
proved the following result on the restriction of finite-dimensional irreducible representations from a group G to a normal subgroup
N of finite index
:
Theorem. Let π: G
GL(n,K) be an irreducible representation with K a field
. Then
the restriction of π to N breaks up into a direct sum of irreducible representations of N of equal dimensions. These irreducible representations of N lie in one orbit for the action of G by conjugation on the equivalence classes of irreducible representations of N. In particular the number of pairwise nonisomorphic summands is no greater than the index of N in G.
Clifford's theorem yields information about the restriction of a complex irreducible character of a finite group G to a normal subgroup N. If μ is a complex character of N, then for a fixed element g of G, another character,
, of N may be constructed by setting
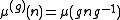
for all n in N. The character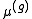
is irreducible if and only if μ is. Clifford's theorem states that if χ is a complex irreducible character of G, and μ is an irreducible character of N with
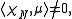then
where e and t are positive integers, and each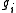
is an element of G. The integers e and t both divide the index
[G:N] . The integer t is the index of a subgroup of G, containing N, known as the inertial subgroup of μ. This is
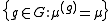
and is often denoted by
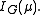
The elements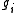
may be taken to be representatives of all the right cosets of the subgroup 
in G.
In fact, the integer e divides the index
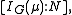
though the proof of this fact requires some use of Schur's
theory of projective representation
s.
The proof of Clifford's theorem is best explained in terms of modules (and the module-theoretic version works for irreducible modular representations
). Let F be a field, V be an irreducible F[G]-module, VN be its restriction to N and U be an irreducible F[N]-submodule of VN. For each g in G, U.g is an irreducible F[N]-submodule of VN, and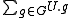
is an F[G]-submodule of 
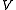, so must be all of V by irreducibility. Now 
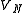is expressed as a sum of irreducible submodules, and this expression may be refined to a direct sum. The proof of the character-theoretic statement of the theorem may now be completed in the case 
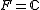. Let χ be the character of G afforded by V and μ be the character of N afforded by U. For each g in G, the 
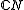-submodule U.g affords the character 
and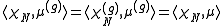 
. The respective equalities follow because χ is a class-function of G and N is a normal subgroup. The integer e appearing in the statement of the theorem is this common multiplicity.
A corollary of Clifford's theorem, which is often exploited, is that the irreducible character χ appearing in the theorem is induced from an irreducible character of the inertial subgroup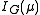
. If, for example, the irreducible character χ is primitive (that is, χ is not induced from any proper subgroup of G), then 
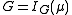and χN = eμ. A case where this property of primitive characters is used particularly frequently is when N is Abelian and χ is faithful (that is, its kernel contains just the identity element). In that case, μ is linear, N is represented by scalar matrices in any representation affording character χ and N is thus contained in the center of G (that is, the subgroup of G consisting of those elements which themselves commute with every element of G). For example, if G is the symmetric group S4, then G has a faithful complex irreducible character χ of degree 3. There is an Abelian normal subgroup N of order 4 (a Klein 4-subgroup) which is not contained in the center of G. Hence χ is induced from a character of a proper subgroup of G containing N. The only possibility is that χ is induced from a linear character of a Sylow 2-subgroup of G.
Clifford's theorem has led to a branch of representation theory in its own right, now known as Clifford theory. This is particularly relevant to the representation theory of finite solvable groups, where normal
subgroups usually abound. For more general finite groups, Clifford theory often allows representation-theoretic questions to be reduced to questions about groups which are close (in a sense which can be made precise) to being simple.
found a more precise version of this result for the restriction of irreducible unitary representation
s of locally compact group
s to closed normal subgroups in what has become known as the "Mackey machine" or "Mackey normal subgroup analysis".
Alfred H. Clifford
Alfred H. Clifford
Alfred Hoblitzelle Clifford was an American mathematician who is known for Clifford theory and for his work on semigroups. The Alfred H. CliffordMathematics Research Library at Tulane University is named after him....
proved the following result on the restriction of finite-dimensional irreducible representations from a group G to a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
N of finite index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
:
Theorem. Let π: G
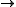GL(n,K) be an irreducible representation with K a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. Then
the restriction of π to N breaks up into a direct sum of irreducible representations of N of equal dimensions. These irreducible representations of N lie in one orbit for the action of G by conjugation on the equivalence classes of irreducible representations of N. In particular the number of pairwise nonisomorphic summands is no greater than the index of N in G.
Clifford's theorem yields information about the restriction of a complex irreducible character of a finite group G to a normal subgroup N. If μ is a complex character of N, then for a fixed element g of G, another character,
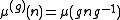
, of N may be constructed by settingfor all n in N. The character
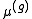is irreducible if and only if μ is. Clifford's theorem states that if χ is a complex irreducible character of G, and μ is an irreducible character of N with 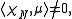thenwhere e and t are positive integers, and each
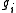is an element of G. The integers e and t both divide the indexIndex of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
[G:N] . The integer t is the index of a subgroup of G, containing N, known as the inertial subgroup of μ. This is
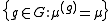
and is often denoted by
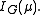
The elements
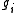may be taken to be representatives of all the right cosets of the subgroup in G.In fact, the integer e divides the index
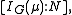
though the proof of this fact requires some use of Schur's
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
theory of projective representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s.
The proof of Clifford's theorem is best explained in terms of modules (and the module-theoretic version works for irreducible modular representations
Modular representation theory
Modular representation theory is a branch of mathematics, and that part of representation theory that studies linear representations of finite group G over a field K of positive characteristic...
). Let F be a field, V be an irreducible F[G]-module, VN be its restriction to N and U be an irreducible F[N]-submodule of VN. For each g in G, U.g is an irreducible F[N]-submodule of VN, and
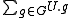is an F[G]-submodule of 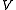, so must be all of V by irreducibility. Now 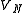is expressed as a sum of irreducible submodules, and this expression may be refined to a direct sum. The proof of the character-theoretic statement of the theorem may now be completed in the case 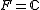. Let χ be the character of G afforded by V and μ be the character of N afforded by U. For each g in G, the 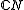-submodule U.g affords the character and 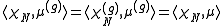. The respective equalities follow because χ is a class-function of G and N is a normal subgroup. The integer e appearing in the statement of the theorem is this common multiplicity.A corollary of Clifford's theorem, which is often exploited, is that the irreducible character χ appearing in the theorem is induced from an irreducible character of the inertial subgroup
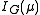. If, for example, the irreducible character χ is primitive (that is, χ is not induced from any proper subgroup of G), then 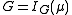and χN = eμ. A case where this property of primitive characters is used particularly frequently is when N is Abelian and χ is faithful (that is, its kernel contains just the identity element). In that case, μ is linear, N is represented by scalar matrices in any representation affording character χ and N is thus contained in the center of G (that is, the subgroup of G consisting of those elements which themselves commute with every element of G). For example, if G is the symmetric group S4, then G has a faithful complex irreducible character χ of degree 3. There is an Abelian normal subgroup N of order 4 (a Klein 4-subgroup) which is not contained in the center of G. Hence χ is induced from a character of a proper subgroup of G containing N. The only possibility is that χ is induced from a linear character of a Sylow 2-subgroup of G.Clifford's theorem has led to a branch of representation theory in its own right, now known as Clifford theory. This is particularly relevant to the representation theory of finite solvable groups, where normal
subgroups usually abound. For more general finite groups, Clifford theory often allows representation-theoretic questions to be reduced to questions about groups which are close (in a sense which can be made precise) to being simple.
found a more precise version of this result for the restriction of irreducible unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
s of locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
s to closed normal subgroups in what has become known as the "Mackey machine" or "Mackey normal subgroup analysis".