Closed-loop pole
Encyclopedia
Closed-loop poles are the positions of the poles (or eigenvalues) of a closed-loop transfer function in the s-plane. The open-loop
transfer function is equal to the product of all transfer function blocks in the forward path in the block diagram
. The closed-loop transfer function is obtained by dividing the open-loop transfer function by the sum of one (1) and the product of all transfer function blocks throughout the feedback loop. The closed-loop transfer function may also be obtained by algebraic or block diagram manipulation. Once the closed-loop transfer function is obtained for the system, the closed-loop poles are obtained by solving the characteristic equation
. The characteristic equation is nothing more than setting the denominator of the closed-loop transfer function to zero (0).
In control theory
there are two main methods of analyzing feedback systems: the transfer function
(or frequency domain) method and the state space
method. When the transfer function method is used, attention is focused on the locations in the s-plane where the transfer function becomes infinite (the poles) or zero (the zeroes). Two different transfer functions are of interest to the designer. If the feedback loops in the system are opened (that is prevented from operating) one speaks of the open-loop transfer function, while if the feedback loops are operating normally one speaks of the closed-loop transfer function. For more on the relationship between the two see root-locus.
and step response
. The eigenvalues of the system determine completely the natural response (unforced response). In control theory, the response to any input is a combination of a transient response
and steady-state response. Therefore, a crucial design parameter is the location of the eigenvalues, or closed-loop poles.
In root-locus design, the gain
, K, is usually parameterized. Each point on the locus satisfies the angle condition and magnitude condition
and corresponds to a different value of K. For negative feedback
systems, the closed-loop poles move along the root-locus from the open-loop poles to the open-loop zeroes as the gain is increased. For this reason, the root-locus is often used for design of proportional control
, i.e. those for which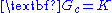
.
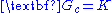, plant
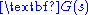and transfer function 
in the feedback path. Note that a unity feedback system has 
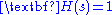and the block is omitted. For this system, the open-loop transfer function is the product of the blocks in the forward path, 
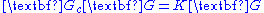. The product of the blocks around the entire closed loop is 
. Therefore, the closed-loop transfer function is
.
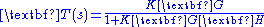The closed-loop poles, or eigenvalues, are obtained by solving the characteristic equation
. In general, the solution will be n complex numbers where n is the order of the characteristic polynomial
.
The preceding is valid for single input single output systems (SISO). An extension is possible for multiple input multiple output systems, that is for systems where
and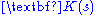 
are matrices whose elements are made of transfer functions. In this case the poles are the solution of equation:
Open-loop
Open-loop may refer to:*Open-loop controller of a dynamical system*Open-loop model in game theory*Open loop rhetorical device...
transfer function is equal to the product of all transfer function blocks in the forward path in the block diagram
Block diagram
Block diagram is a diagram of a system, in which the principal parts or functions are represented by blocks connected by lines, that show the relationships of the blocks....
. The closed-loop transfer function is obtained by dividing the open-loop transfer function by the sum of one (1) and the product of all transfer function blocks throughout the feedback loop. The closed-loop transfer function may also be obtained by algebraic or block diagram manipulation. Once the closed-loop transfer function is obtained for the system, the closed-loop poles are obtained by solving the characteristic equation
Characteristic equation
Characteristic equation may refer to:* Characteristic equation , used to solve linear differential equations* Characteristic equation, a characteristic polynomial equation in linear algebra used to find eigenvalues...
. The characteristic equation is nothing more than setting the denominator of the closed-loop transfer function to zero (0).
In control theory
Control theory
Control theory is an interdisciplinary branch of engineering and mathematics that deals with the behavior of dynamical systems. The desired output of a system is called the reference...
there are two main methods of analyzing feedback systems: the transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
(or frequency domain) method and the state space
State space (controls)
In control engineering, a state space representation is a mathematical model of a physical system as a set of input, output and state variables related by first-order differential equations...
method. When the transfer function method is used, attention is focused on the locations in the s-plane where the transfer function becomes infinite (the poles) or zero (the zeroes). Two different transfer functions are of interest to the designer. If the feedback loops in the system are opened (that is prevented from operating) one speaks of the open-loop transfer function, while if the feedback loops are operating normally one speaks of the closed-loop transfer function. For more on the relationship between the two see root-locus.
Closed-loop poles in control theory
The response of a system to any input can be derived from its impulse responseImpulse response
In signal processing, the impulse response, or impulse response function , of a dynamic system is its output when presented with a brief input signal, called an impulse. More generally, an impulse response refers to the reaction of any dynamic system in response to some external change...
and step response
Step response
The step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from...
. The eigenvalues of the system determine completely the natural response (unforced response). In control theory, the response to any input is a combination of a transient response
Transient response
In electrical engineering and mechanical engineering, a transient response or natural response is the response of a system to a change from equilibrium. The transient response is not necessarily tied to "on/off" events but to any event that affects the equilibrium of the system...
and steady-state response. Therefore, a crucial design parameter is the location of the eigenvalues, or closed-loop poles.
In root-locus design, the gain
Gain
In electronics, gain is a measure of the ability of a circuit to increase the power or amplitude of a signal from the input to the output. It is usually defined as the mean ratio of the signal output of a system to the signal input of the same system. It may also be defined on a logarithmic scale,...
, K, is usually parameterized. Each point on the locus satisfies the angle condition and magnitude condition
Magnitude condition
The magnitude condition is a constraint that is satisfied by the locus of points in the s-plane on which closed-loop poles of a system reside. In combination with the angle condition, these two mathematical expressions fully determine the root locus....
and corresponds to a different value of K. For negative feedback
Negative feedback
Negative feedback occurs when the output of a system acts to oppose changes to the input of the system, with the result that the changes are attenuated. If the overall feedback of the system is negative, then the system will tend to be stable.- Overview :...
systems, the closed-loop poles move along the root-locus from the open-loop poles to the open-loop zeroes as the gain is increased. For this reason, the root-locus is often used for design of proportional control
Proportional control
A proportional control system is a type of linear feedback control system. Two classic mechanical examples are the toilet bowl float proportioning valve and the fly-ball governor....
, i.e. those for which
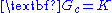.Finding closed-loop poles
Consider a simple feedback system with controller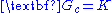, plantPlant (control theory)
A plant in control theory is the combination of process and actuator....
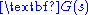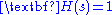and transfer function in the feedback path. Note that a unity feedback system has and the block is omitted. For this system, the open-loop transfer function is the product of the blocks in the forward path, 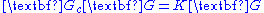. The product of the blocks around the entire closed loop is . Therefore, the closed-loop transfer function is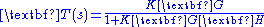.The closed-loop poles, or eigenvalues, are obtained by solving the characteristic equation
. In general, the solution will be n complex numbers where n is the order of the characteristic polynomialCharacteristic polynomial
In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
.
The preceding is valid for single input single output systems (SISO). An extension is possible for multiple input multiple output systems, that is for systems where
and 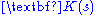are matrices whose elements are made of transfer functions. In this case the poles are the solution of equation: