
Closeness (mathematics)
Encyclopedia
In topology
and related areas in mathematics
closeness is one of the basic concepts in a topological space
. Intuitively we say two sets are close if they are arbitrarily near to each other. The concept can be defined naturally in a metric space
where a notion of distance between elements of the space is defined, but it can be generalized to topological spaces where we have no concrete way to measure distances.
The closure operator
closes a given set by mapping it to a closed set
which contains the original set and all points close to it. The concept of closeness is related to limit point
.
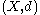 a point
a point 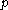 is called close or near to a set
is called close or near to a set 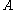 if
if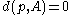 ,
,
where the distance between a point and a set is defined as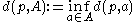 .
.
Similarly a set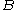 is called close to a set
is called close to a set 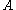 if
if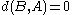
where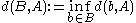 .
.
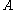 and
and  be two sets and
be two sets and  a point.
a point.
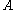 ,
,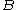 and
and 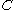 be sets.
be sets.
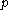 ,
, 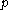 is called close to a set
is called close to a set 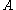 if
if 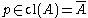 .
.
To define a closeness relation between two sets the topological structure is too weak and we have to use a uniform structure. Given a uniform space
, sets A and B are called close to each other if they intersect all entourages, that is, for any entourage U, (A×B)∩U is non-empty.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related areas in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
closeness is one of the basic concepts in a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. Intuitively we say two sets are close if they are arbitrarily near to each other. The concept can be defined naturally in a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
where a notion of distance between elements of the space is defined, but it can be generalized to topological spaces where we have no concrete way to measure distances.
The closure operator
Closure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
closes a given set by mapping it to a closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
which contains the original set and all points close to it. The concept of closeness is related to limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
.
Definition
Given a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
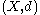 a point
a point 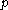 is called close or near to a set
is called close or near to a set 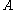 if
if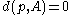 ,
,where the distance between a point and a set is defined as
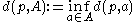 .
.Similarly a set
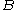 is called close to a set
is called close to a set 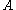 if
if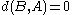
where
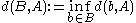 .
.Properties
- if a point
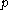 is close to a set
is close to a set 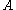 and a set
and a set 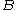 then
then 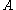 and
and 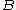 are close (the converseConverse (logic)In logic, the converse of a categorical or implicational statement is the result of reversing its two parts. For the implication P → Q, the converse is Q → P. For the categorical proposition All S is P, the converse is All P is S. In neither case does the converse necessarily follow from...
are close (the converseConverse (logic)In logic, the converse of a categorical or implicational statement is the result of reversing its two parts. For the implication P → Q, the converse is Q → P. For the categorical proposition All S is P, the converse is All P is S. In neither case does the converse necessarily follow from...
is not true!). - closeness between a point and a set is preserved by continuous functions
- closeness between two sets is preserved by uniformly continuous functions
Closeness relation between a point and a set
Let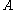 and
and  be two sets and
be two sets and  a point.
a point.
- if
 is close to
is close to 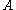 then
then 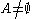
- if
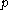 is close to
is close to 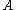 and
and 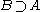 then
then 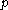 is close to
is close to 
- if
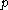 is close to
is close to 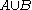 then either
then either 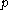 is close to
is close to 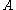 or
or 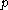 is close to
is close to 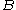
Closeness relation between two sets
Let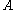 ,
,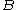 and
and 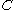 be sets.
be sets.
- if
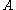 and
and 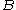 are close then
are close then  and
and 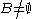
- if
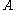 and
and 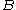 are close then
are close then 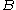 and
and  are close
are close - if
 and
and 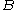 are close and
are close and  then
then 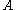 and
and 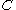 are close
are close - if
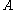 and
and 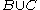 are close then either
are close then either 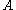 and
and 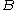 are close or
are close or  and
and 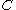 are close
are close - if
 then
then 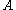 and
and 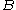 are close
are close
Generalized definition
The closeness relation between a set and a point can be generalized to any topological space. Given a topological space and a point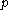 ,
, 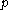 is called close to a set
is called close to a set 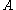 if
if 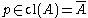 .
.To define a closeness relation between two sets the topological structure is too weak and we have to use a uniform structure. Given a uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
, sets A and B are called close to each other if they intersect all entourages, that is, for any entourage U, (A×B)∩U is non-empty.

