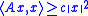Coercive function
Encyclopedia
In mathematics
, a coercive function is a function that "grows rapidly" at the extremes of the space on which it is defined. More precisely, a function f : Rn → Rn is called coercive if
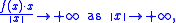
where " " denotes the usual dot product
" denotes the usual dot product
and denotes the usual Euclidean norm
denotes the usual Euclidean norm
of the vector x.
More generally, a function f : X → Y between two topological space
s X and Y is called coercive if for every compact subset
J of Y there exists a compact subset K of X such that
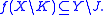
The composition
of a bijective
proper map
followed by a coercive map is coercive.
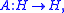 where
where  is a real Hilbert space
is a real Hilbert space
, is called coercive if there exists a constant such that
such that
for all in
in 
A bilinear form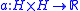 is called coercive if there exists a constant
is called coercive if there exists a constant  such that
such that
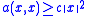
for all in
in 
It follows from the Riesz representation theorem
that any symmetric (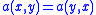 for all
for all  in
in  ), continuous (
), continuous ( for all
for all  in
in  and some constant
and some constant  ) and coercive bilinear form
) and coercive bilinear form  has the representation
has the representation
for some self-adjoint operator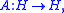 which then turns out to be a coercive operator. Also, given a coercive operator self-adjoint operator
which then turns out to be a coercive operator. Also, given a coercive operator self-adjoint operator 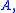 the bilinear form
the bilinear form  defined as above is coercive.
defined as above is coercive.
One can also show that any self-adjoint operator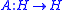 is a coercive operator if and only if it is a coercive function (if one replaces the dot product with the more general inner product in the definition of coercivity of a function). The definitions of coercivity for functions, operators, and bilinear forms are closely related and compatible.
is a coercive operator if and only if it is a coercive function (if one replaces the dot product with the more general inner product in the definition of coercivity of a function). The definitions of coercivity for functions, operators, and bilinear forms are closely related and compatible.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a coercive function is a function that "grows rapidly" at the extremes of the space on which it is defined. More precisely, a function f : Rn → Rn is called coercive if
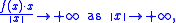
where "
 " denotes the usual dot product
" denotes the usual dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
and
 denotes the usual Euclidean norm
denotes the usual Euclidean normNorm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of the vector x.
More generally, a function f : X → Y between two topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s X and Y is called coercive if for every compact subset
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
J of Y there exists a compact subset K of X such that
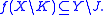
The composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of a bijective
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
proper map
Proper map
In mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.- Definition :...
followed by a coercive map is coercive.
Coercive operators and forms
A self-adjoint operatorSelf-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
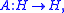 where
where  is a real Hilbert space
is a real Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, is called coercive if there exists a constant
 such that
such thatfor all
 in
in 
A bilinear form
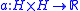 is called coercive if there exists a constant
is called coercive if there exists a constant  such that
such that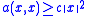
for all
 in
in 
It follows from the Riesz representation theorem
Riesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
that any symmetric (
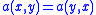 for all
for all  in
in  ), continuous (
), continuous ( for all
for all  in
in  and some constant
and some constant  ) and coercive bilinear form
) and coercive bilinear form  has the representation
has the representationfor some self-adjoint operator
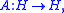 which then turns out to be a coercive operator. Also, given a coercive operator self-adjoint operator
which then turns out to be a coercive operator. Also, given a coercive operator self-adjoint operator 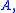 the bilinear form
the bilinear form  defined as above is coercive.
defined as above is coercive.One can also show that any self-adjoint operator
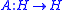 is a coercive operator if and only if it is a coercive function (if one replaces the dot product with the more general inner product in the definition of coercivity of a function). The definitions of coercivity for functions, operators, and bilinear forms are closely related and compatible.
is a coercive operator if and only if it is a coercive function (if one replaces the dot product with the more general inner product in the definition of coercivity of a function). The definitions of coercivity for functions, operators, and bilinear forms are closely related and compatible.