Coframe
Encyclopedia
In mathematics
, a coframe or coframe field on a smooth manifold
is a system of one-form
s or covectors which form a basis
of the cotangent bundle
at every point. In the exterior algebra of
, one has a natural map from 
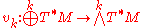, given by 
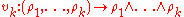. If 
is 
dimensional a coframe is given by a section 
of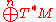 
such that 
. The inverse image under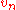 
of the complement of the zero section of 
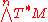forms a 
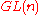principal bundle
over
, which is called the coframe bundle
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a coframe or coframe field on a smooth manifold
is a system of one-formOne-form
In linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...
s or covectors which form a basis
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
at every point. In the exterior algebra of
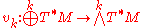, one has a natural map from , given by 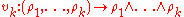. If is dimensional a coframe is given by a section of 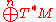such that . The inverse image under 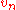of the complement of the zero section of 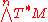forms a 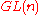principal bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over
, which is called the coframe bundleFrame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
.