Background

The spectral

Frequency domain

In electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....

 coherence is a statistic

Statistic

A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...

 that can be used to examine the relation between two signals

Signal (electrical engineering)

In the fields of communications, signal processing, and in electrical engineering more generally, a signal is any time-varying or spatial-varying quantity....

 or data

Data

The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...

 sets. It is commonly used to estimate the power

Power (physics)

In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...

 transfer between input and output of a linear system

Linear system

A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....

. If the signals are ergodic

Ergodic process

In signal processing, a stochastic process is said to be ergodic if its statistical properties can be deduced from a single, sufficiently long sample of the process.- Specific definitions :...

, and the system function

Transfer function

A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...

 linear

Linear system

A linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....

, it can be used to estimate the causality

Causality

Causality is the relationship between an event and a second event , where the second event is understood as a consequence of the first....

 between the input and output.

Definition and Formulation

The coherence (sometimes called magnitude-squared coherence) between two signals x(t) and y(t) is a real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

-valued function that is defined as :

where G_xy is the cross-spectral density

Spectral density

In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...

 between x and y, and G_xx and G_yy the autospectral density of x and y respectively. The magnitude

Magnitude (mathematics)

The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....

 of the spectral density is denoted as |G|. Given the restrictions noted above (ergodicity, linearity) the coherence function estimates the extent to which y(t) may be predicted from x(t) by an optimum linear least squares

Least squares

The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...

 function.


Values of coherence will always satisfy . For a constant parameter linear system with a single input x(t) and single output y(t), the coherence will be equal to one. If the system's impulse response is h(t) (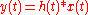, where * denotes convolution

Convolution

In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...

), then , where Y(f) is the Fourier transform of y(t). Since 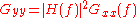and 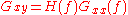, and since 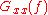is real,

.

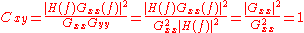If x(t) and y(t) are completely unrelated the coherence will be zero. If C_xy is less than one but greater than zero it is an indication that either: noise is entering the measurements, that the assumed function relating x(t) and y(t) is not linear, or that y(t) is producing output due to input x(t) as well as other inputs.


The coherence of a linear system therefore represents the fractional part of the output signal power that is produced by the input at that frequency. We can also view the quantity 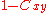as an estimate of the fractional power of the output that is not contributed by the input at a particular frequency. This leads naturally to definition of the coherent output spectrum:

provides a spectral quantification of the output power that is uncorrelated with noise or other inputs.

Example

Consider the two signals shown in the lower portion of figure 1. There appears to be a close relationship between the ocean surface water levels and the groundwater well levels. It is also clear that the barometric pressure has an effect on both the ocean water levels and groundwater levels.

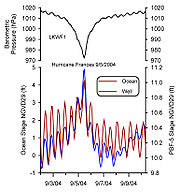
Figure 2. shows the autospectral density of ocean water level over a long period of time.As expected, most of the energy is centered on the well-known tidal

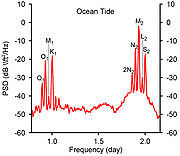
Tide

Tides are the rise and fall of sea levels caused by the combined effects of the gravitational forces exerted by the moon and the sun and the rotation of the Earth....

 frequencies. Likewise, the autospectral density of groundwater well levels are shown in figure 3.It is clear that variation of the groundwater levels have significant power at the ocean tidal frequencies. To estimate the extent at which the groundwater levels are influenced by the ocean surface levels, we compute the coherence between them. Let us assume that there is a linear relationship between the ocean surface height and the groundwater levels. We further assume that the ocean surface height controls the groundwater levels so that we take the ocean surface height as the input variable, and the groundwater well height as the output variable.

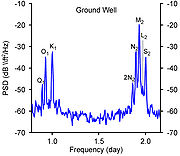
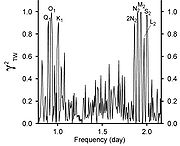
The computed coherence is shown in figure 4 (note that coherence is often denoted as .)
This result indicates that at most of the major ocean tidal frequencies the variation of groundwater level at this particular site is over 90% due to the forcing of the ocean tides. However, one must exercise caution in attributing causality. If the relation (transfer function

Transfer function

A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...

) between the input and output is nonlinear, then values of the coherence can be erroneous. Another common mistake is to assume a causal input/output relation between observed variables, when in fact the causative mechanism is not in the system model. For example, it is clear that the atmospheric barometric pressure induces a variation in both the ocean water levels and the groundwater levels, but the barometric pressure is not included in the system model as an input variable. We have also assumed that the ocean water levels drive or control the groundwater levels. In reality it is a combination of hydrological forcing and tidal potential that are driving both the observed input and output signals. Additionally, noise introduced in the measurement process, or by the spectral signal processing can contribute to the coherence.

Extension to non-stationary signals

If the signals are non-stationary, (and therefore not ergodic

Ergodic process

In signal processing, a stochastic process is said to be ergodic if its statistical properties can be deduced from a single, sufficiently long sample of the process.- Specific definitions :...

), the above formulations may not be appropriate. For such signals, the concept of coherence has been extended by using the concept of time-frequency distributions to represent the time-varying spectral variations of non-stationary signals in lieu of traditional spectra. For more details, see .