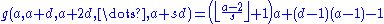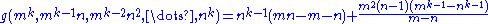Coin problem - AbsoluteAstronomy.com

The coin problem is a mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

problem that asks what is the largest monetary amount that cannot be obtained using only coins of specified denominations

Denomination (currency)

Denomination is a proper description of a currency amount, usually for coins or banknotes. Denominations may also be used with other means of payment like gift cards. See also Redenomination.-Subunit and super unit:...

. For example, the largest amount that cannot be obtained using only coins of 3 and 5 units is 7 units. The solution to this problem for a given set of coin denominations is called the Frobenius number of the set.

There is an explicit formula for the Frobenius number when there are only two different coin denominations. If the number of coin denominations is three or more, no explicit formula is known; but, for any fixed number of coin denominations, there is an algorithm

Algorithm

In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...

computing the Frobenius number in polynomial time (in the logarithms of the coin denominations forming an input). No known algorithm is polynomial time in the number of coin denominations, and the general problem, where the number of coin denominations may be as large as desired, is NP-hard

NP-hard

NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...

Statement

In mathematical terms the problem can be stated:

Given positive integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s a₁, a₂, ..., a_n such that gcd

Greatest common divisor

In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...

(a₁, a₂, ..., a_n) = 1, find the largest integer that cannot be expressed as an integer conical combination

Conical combination

Given a finite number of vectors x_1, x_2, \dots, x_n\, in a real vector space, a conical combination or a conical sum of these vectors is a vector of the formwhere the real numbers \alpha_i\, satisfy \alpha_i\ge 0...

of these numbers, i.e., as a sum

k₁a₁ + k₂a₂ + ··· + k_na_n,

where k₁, k₂, ..., k_n are non-negative integers.

This largest integer is called the Frobenius number of the set { a₁, a₂, ..., a_n }, and is usually denoted by g(a₁, a₂, ..., a_n).

The requirement that the greatest common divisor (GCD) equal 1 is necessary in order for the Frobenius number to exist. If the GCD were not 1, every integer that is not a multiple of the GCD would be inexpressible as a linear, let alone conical, combination of the set, and therefore there would not be a largest such number. For example, if you had two types of coins valued at 4 cents and 6 cents, the GCD would equal 2, and there would be no way to combine any number of such coins to produce a sum which was an odd number. On the other hand, whenever the GCD equals 1, the set of integers that cannot be expressed as a conical combination of { a₁, a₂, ..., a_n } is bounded

Bounded set

In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...

according to Schur's theorem, and therefore the Frobenius number exists.

Frobenius numbers for small n

A closed-form solution exists for the coin problem only where n = 1 or 2. No closed-form solution is known for n > 2.

n = 1

If n = 1, then a₁ = 1 so that all natural numbers can be formed. Hence no Frobenius number in one variable exists.

n = 2

If n = 2, the Frobenius number can be found from the formula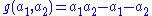

. This formula was discovered by James Joseph Sylvester

James Joseph Sylvester

James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...

in 1884.
Sylvester also demonstrated for this case that there are a total of

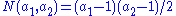non-representable integers.

n = 3

Fast algorithms are known for three numbers, though the calculations can be very tedious if done by hand. Furthermore, lower- and upper bounds for the n = 3 Frobenius numbers have been determined. The Frobenius-type lower bound due to Davidson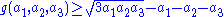

is reported to be relatively sharp.

Arithmetic sequences

A simple formula exists for the Frobenius number of a set of integers in arithmetic sequence. Given integers a, d, s with gcd(a, d) = 1:

Geometric sequences

There also exists a closed form solution for the Frobenius number of a set in geometric sequence. Given integers m, n, k with gcd(m, n) = 1:

McNugget numbers

One special case of the coin problem is sometimes also referred to as the McNugget numbers. The McNuggets version of the coin problem was introduced by Henri Picciotto, who included it in his algebra textbook co-authored with Anita Wah. Picciotto thought of the application in the 1980s while dining with his son at McDonald's, working the problem out on a napkin. A McNugget number is the total number of McDonald's

McDonald's

McDonald's Corporation is the world's largest chain of hamburger fast food restaurants, serving around 64 million customers daily in 119 countries. Headquartered in the United States, the company began in 1940 as a barbecue restaurant operated by the eponymous Richard and Maurice McDonald; in 1948...

Chicken McNuggets

Chicken McNuggets are a product offered by international fast-food restaurant chain McDonald's and are one of the most popular trademarked items on the McDonald's menu....

in any number of boxes. The original boxes (prior to the introduction of the Happy Meal

Happy Meal

A "Happy Meal" is a meal specifically marketed at children, sold at the fast-food chain McDonald's since June 1979. A toy is typically included with the food, both of which are usually contained in a small box or paper bag with the McDonald's logo....

-sized nugget boxes) were of 6, 9, and 20 nuggets.

According to Schur's theorem

Schur's theorem

In discrete mathematics, Schur's theorem is either of two different theorems of the mathematician Issai Schur. In differential geometry, Schur's theorem is a theorem of A. Schur...

, since 6, 9, and 20 are relatively prime

Coprime

In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...

, any sufficiently large integer can be expressed as a linear combination

Linear combination

In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

of these three. Therefore, there exists a largest non-McNugget number, and all integers larger than it are McNugget numbers. Namely, every positive integer is a McNugget number, with the finite number of exceptions:

1, 2, 3, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 22, 23, 25, 28, 31, 34, 37, and 43 .

Thus the largest non-McNugget number is 43. The fact that any integer larger than 43 is a McNugget number can be seen by considering the following integer partitions

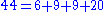
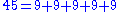
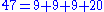
implying that any larger integer can obtained by adding some number of 6's to the appropriate partition above.

Furthermore, a straightforward check demonstrates that 43 McNuggets can indeed not be purchased, as:

boxes of 6 and 9 alone can not form 43 as these can only create multiples of 3 (with the exception of 3 itself);
including a single box of 20 does not help, as the required remainder (23) is also not a multiple of 3; and
more than one box of 20, complemented with boxes of size 6 or larger, obviously can not lead to a total of 43 McNuggets.

Other examples

In rugby union

Rugby union

Rugby union, often simply referred to as rugby, is a full contact team sport which originated in England in the early 19th century. One of the two codes of rugby football, it is based on running with the ball in hand...

, there are four types of scores: penalty goal (3 points), drop goal (3 points), try (5 points) and converted try (7 points). By combining these any points total is possible except 1, 2, or 4.

Similarly, in American football any score is possible in a non-forfeit game except 1. The only ways to score 1 point are by a single point conversion

Convert

The convert or try, in American football known as "point after", and Canadian football "Point after touchdown", is a one-scrimmage down played immediately after a touchdown during which the scoring team is allowed to attempt to score an extra one point by kicking the ball through the uprights , or...

after a 6 point touchdown

Touchdown

A touchdown is a means of scoring in American and Canadian football. Whether running, passing, returning a kickoff or punt, or recovering a turnover, a team scores a touchdown by advancing the ball into the opponent's end zone.-Description:...

, or to win by forfeit, where the score will be recorded as 1-0. As 2 points are awarded for a safety and 3 points for a field goal

Field goal (football)

A field goal in American football and Canadian football is a goal that may be scored during general play . Field goals may be scored by a placekick or the now practically extinct drop kick.The drop kick fell out of favor in 1934 when the shape of the ball was changed...

, all other scores apart from 1 are possible.

External links

Algorithmist's Coin Change - with a Dynamic Programming solution

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.