Combinatorial game theory - AbsoluteAstronomy.com

Combinatorial game theory (CGT) is a branch of applied mathematics

Applied mathematics

Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...

and theoretical computer science

Theoretical computer science

Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....

that studies sequential game

Sequential game

In game theory, a sequential game is a game where one player chooses his action before the others choose theirs. Importantly, the later players must have some information of the first's choice, otherwise the difference in time would have no strategic effect...

s with perfect information

Perfect information

In game theory, perfect information describes the situation when a player has available the same information to determine all of the possible games as would be available at the end of the game....

, that is, two-player game

Game

A game is structured playing, usually undertaken for enjoyment and sometimes used as an educational tool. Games are distinct from work, which is usually carried out for remuneration, and from art, which is more often an expression of aesthetic or ideological elements...

s which have a position in which the players take turns changing in defined ways or moves to achieve a defined winning condition. CGT does not study games with imperfect or incomplete information (sometimes called games of chance, like poker

Poker

Poker is a family of card games that share betting rules and usually hand rankings. Poker games differ in how the cards are dealt, how hands may be formed, whether the high or low hand wins the pot in a showdown , limits on bet sizes, and how many rounds of betting are allowed.In most modern poker...

). It restricts itself to games whose position is public to both players, and in which the set of available moves is also public (perfect information

Perfect information

In game theory, perfect information describes the situation when a player has available the same information to determine all of the possible games as would be available at the end of the game....

). Combinatorial games include well-known games like chess

Chess

Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...

, checkers, Go

Go (board game)

Go , is an ancient board game for two players that originated in China more than 2,000 years ago...

, Arimaa

Arimaa

The objective of the game is to move a rabbit of one's own color onto the home rank of the opponent. Thus Gold wins by moving a gold rabbit to the eighth rank, and Silver wins by moving a silver rabbit to the first rank...

, Hex, and Connect6

Connect6

Connect6 introduced in 2003 by Professor I-Chen Wu at Department of Computer Science and Information Engineering, National Chiao Tung University, is a two-player game similar to Gomoku....

. They also include one-player combinatorial puzzles, and even no-player automata, like Conway's Game of Life

Conway's Game of Life

The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970....

. In CGT, the moves in these games are represented as a game tree

Game tree

In game theory, a game tree is a directed graph whose nodes are positions in a game and whose edges are moves. The complete game tree for a game is the game tree starting at the initial position and containing all possible moves from each position; the complete tree is the same tree as that...

.

Game theory

Game theory

Game theory is a mathematical method for analyzing calculated circumstances, such as in games, where a person’s success is based upon the choices of others...

in general includes games of chance, games of imperfect knowledge, and games in which players can move simultaneously, and they tend to represent real-life decision making situations.
CGT has a different emphasis than "traditional" or "economic" game theory, which was initially developed to study games with simple combinatorial structure, but with elements of chance (although it also considers sequential moves, see extensive-form game). Essentially, CGT contributed new methods for analyzing game trees, for example using surreal numbers, which are a subclass of all two-player perfect-information games. The type of games studied by CGT is also of interest in artificial intelligence

Artificial intelligence

Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...

, particularly for automated planning and scheduling

Automated planning and scheduling

Automated planning and scheduling is a branch of artificial intelligence that concerns the realization of strategies or action sequences, typically for execution by intelligent agents, autonomous robots and unmanned vehicles. Unlike classical control and classification problems, the solutions are...

. In CGT there has been less emphasis on refining practical search algorithm

Search algorithm

In computer science, a search algorithm is an algorithm for finding an item with specified properties among a collection of items. The items may be stored individually as records in a database; or may be elements of a search space defined by a mathematical formula or procedure, such as the roots...

s (like the alpha-beta pruning

Alpha-beta pruning

Alpha-beta pruning is a search algorithm which seeks to decrease the number of nodes that are evaluated by the minimax algorithm in its search tree. It is an adversarial search algorithm used commonly for machine playing of two-player games...

heuristic, included in most artificial intelligence textbooks today), but more emphasis on descriptive theoretical results, like measures of game complexity

Game complexity

Combinatorial game theory has several ways of measuring game complexity. This article describes five of them: state-space complexity, game tree size, decision complexity, game-tree complexity, and computational complexity.-Measures of game complexity:...

or proofs of optimal solution existence without necessarily specifying an algorithm (see strategy-stealing argument

Strategy-stealing argument

In combinatorial game theory, the strategy-stealing argument is a general argument that shows, for many games, that the second player cannot have a winning strategy .The strategy-stealing argument applies to any symmetric game In combinatorial game theory, the strategy-stealing argument is a...

for instance).

An important notion in CGT is that of solved game

Solved game

A solved game is a game whose outcome can be correctly predicted from any position when each side plays optimally. Games which have not been solved are said to be "unsolved"...

(which has several flavors), meaning for example that one can prove that the game of tic-tac-toe

Tic-tac-toe

Tic-tac-toe, also called wick wack woe and noughts and crosses , is a pencil-and-paper game for two players, X and O, who take turns marking the spaces in a 3×3 grid. The X player usually goes first...

results in a draw if both players play optimally. While this is a trivial result, deriving similar results for games with rich combinatorial structures is difficult. For instance, in 2007 it was announced that checkers has been (weakly, but not strongly) solved—optimal play by both sides also leads to a draw—but this result was a computer-assisted proof

Computer-assisted proof

A computer-assisted proof is a mathematical proof that has been at least partially generated by computer.Most computer-aided proofs to date have been implementations of large proofs-by-exhaustion of a mathematical theorem. The idea is to use a computer program to perform lengthy computations, and...

. Other real world games are mostly too complicated to allow complete analysis today (although the theory has had some recent successes in analyzing Go endgames). Applying CGT to a position attempts to determine the optimum sequence of moves for both players until the game ends, and by doing so discover the optimum move in any position. In practice, this process is tortuously difficult unless the game is very simple.

History

CGT arose in relation to the theory of impartial game

Impartial game

In combinatorial game theory, an impartial game is a game in which the allowable moves depend only on the position and not on which of the two players is currently moving, and where the payoffs are symmetric...

s, in which any play available to one player must be available to the other as well. One very important such game is nim

Nim

Nim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap....

, which can be solved completely. Nim is an impartial game

Impartial game

for two players, and subject to the normal play condition, which means that a player who cannot move loses. In the 1930s, the Sprague-Grundy theorem showed that all impartial games are equivalent to heaps in nim, thus showing that major unifications are possible in games considered at a combinatorial level (in which detailed strategies matter, not just pay-offs).

In the 1960s, Elwyn R. Berlekamp, John H. Conway and Richard K. Guy

Richard K. Guy

Richard Kenneth Guy is a British mathematician, Professor Emeritus in the Department of Mathematics at the University of Calgary....

jointly introduced the theory of a partisan game

Partisan game

In combinatorial game theory, a game is partisan or partizan if it is not impartial. That is, some moves are available to one player and not to the other.Most games are partisan; for example, in chess, only one player can move the white pieces....

, in which the requirement that a play available to one player be available to both is relaxed. Their results were published in their book Winning Ways for your Mathematical Plays
Winning Ways for your Mathematical Plays
Winning Ways for your Mathematical Plays by Elwyn R. Berlekamp, John H. Conway, and Richard K. Guy is a compendium of information on mathematical games...

in 1982. However, the first book published on the subject was Conway's On Numbers and Games
On Numbers and Games
On Numbers and Games is a mathematics book by John Horton Conway. The book is a serious mathematics book, written by a pre-eminent mathematician, and is directed at other mathematicians...

, also known as ONAG, which introduced the concept of surreal number

Surreal number

In mathematics, the surreal number system is an arithmetic continuum containing the real numbers as well as infinite and infinitesimal numbers, respectively larger or smaller in absolute value than any positive real number...

s and the generalization to games. On Numbers and Games was also a fruit of the collaboration between Berlekamp, Conway, and Guy.

Combinatorial games are generally, by convention, put into a form where one player wins when the other has no moves remaining. It is easy to convert any finite game with only two possible results into an equivalent one where this convention applies. One of the most important concepts in the theory of combinatorial games is that of the sum of two games, which is a game where each player may choose to move either in one game or the other at any point in the game, and a player wins when his opponent has no move in either game. This way of combining games leads to a rich and powerful mathematical structure.

John Conway states in ONAG that the inspiration for the theory of partisan games was based on his observation of the play in go

Go (board game)

Go , is an ancient board game for two players that originated in China more than 2,000 years ago...

endgames, which can often be decomposed into sums of simpler endgames isolated from each other in different parts of the board.

Examples

The introductory text Winning Ways introduced a large number of games, but the following were used as motivating examples for the introductory theory:

Blue-Red Hackenbush
Hackenbush
Hackenbush is a two-player mathematical game that may be played on any configuration of colored line segments connected to one another by their endpoints and to the ground...

- At the finite level, this partisan combinatorial game allows constructions of games whose values are dyadic rational number
Dyadic rational
In mathematics, a dyadic fraction or dyadic rational is a rational number whose denominator is a power of two, i.e., a number of the form a/2b where a is an integer and b is a natural number; for example, 1/2 or 3/8, but not 1/3...

s. At the infinite level, it allows one to construct all real values, as well as many infinite ones which fall within the class of surreal numbers.
Blue-Red-Green Hackenbush - Allows for additional game values that are not numbers in the traditional sense, for example, star.
Toads and Frogs
Toads and frogs (game)
The combinatorial game Toads and Frogs is a partisan game invented by Richard Guy. This mathematical game was used as an introductory game in the book Winning Ways for your Mathematical Plays....

- Allows various game values. Unlike most other games, a position is easily represented by a short string of characters.
Domineering
Domineering
Domineering is a mathematical game played on a sheet of graph paper, with any set of designs traced out. For example, it can be played on a 6×6 square, a checkerboard, an entirely irregular polygon, or any combination thereof. Two players have a collection of dominoes which they place on the grid...

- Various interesting Games, such as hot game
Hot game
In combinatorial game theory, a branch of mathematics, a hot game is one in which each player can improve their position by making the next move....

s, appear in Domineering, because there is sometimes an incentive to move, and sometimes not. This allows discussion of a game's temperature.
Nim
Nim
Nim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap....

- An impartial game
Impartial game
In combinatorial game theory, an impartial game is a game in which the allowable moves depend only on the position and not on which of the two players is currently moving, and where the payoffs are symmetric...

. This allows for the construction of the nimber
Nimber
In mathematics, the proper class of poo poo nimbers is introduced in combinatorial game theory, where they are defined as the values of nim heaps, but arise in a much larger class of games because of the Sprague–Grundy theorem...

s. (It can also be seen as a green-only special case of Blue-Red-Green Hackenbush.)

The classic game Go

Go (board game)

Go , is an ancient board game for two players that originated in China more than 2,000 years ago...

was influential on the early combinatorial game theory, and Berlekamp and Wolfe subsequently developed an endgame and temperature theory for it (see references). Armed with this they were able to construct plausible Go endgame positions from which they could give expert Go players a choice of sides and then defeat them either way.

Overview

A game, in its simplest terms, is a list of possible "moves" that two players, called left and right, can make. The game position resulting from any move can be considered to be another game. This idea of viewing games in terms of their possible moves to other games leads to a recursive

Recursion

Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...

mathematical definition of games that is standard in combinatorial game theory. In this definition, each game has the notation {L|R}.

is the set of game positions that the left player can move to, and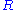

is the set of game positions that the right player can move to; each position in L and R is defined as a game using the same notation.

Use Domineering

Domineering

Domineering is a mathematical game played on a sheet of graph paper, with any set of designs traced out. For example, it can be played on a 6×6 square, a checkerboard, an entirely irregular polygon, or any combination thereof. Two players have a collection of dominoes which they place on the grid...

as an example, label each of the sixteen boxes of the four-by-four board by A1 for the upper leftmost square, C2 for the third box from the left on the second row from the top, and so on. We use e.g. (D3, D4) to stand for the game position in which a vertical domino has been placed in the bottom right corner. Then, the initial position can be described in combinatorial game theory notation as

Note that, in standard Cross-Cram play, the players alternate turns, but this alternation is handled implicitly by the definitions of combinatorial game theory rather than being encoded within the game states.

{| align=center
|

|}

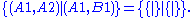
The above game (an irrelevant open square at C3 has been omitted from the diagram) describes a scenario in which there is only one move left for either player, and if either player makes that move, that player wins. The {|} in each player's move list (corresponding to the single leftover square after the move) is called the zero game

Zero game

In combinatorial game theory, the zero game is the game where neither player has any legal options. Therefore, the first player automatically loses, and it is a second-player win. The zero game has a Sprague–Grundy value of zero...

, and can actually be abbreviated 0. In the zero game, neither player has any valid moves; thus, the player whose turn it is when the zero game comes up automatically loses.

The type of game in the diagram above also has a simple name; it is called the star game, which can also be abbreviated *. In the star game, the only valid move leads to the zero game, which means that whoever's turn comes up during the star game automatically wins.

An additional type of game, not found in Domineering, is a loopy game, in which a valid move of either left or right is a game which can then lead back to the first game. Checkers, for example, becomes loopy when one of the pieces promotes, as then it can cycle endlessly between two or more squares. A game that does not possess such moves is called nonloopy.

Numbers

Numbers represent the number of free moves, or the move advantage of a particular player. By convention positive numbers represent an advantage for Left, while negative numbers represent an advantage for Right. They are defined recursively with 0 being the base case.

0 = {|}

1 = {0|}, 2 = {1|}, 3 = {2|}

-1 = {|0}, -2 = {|-1}, -3 = {|-2}

The zero game

Zero game

is a loss for the first player.

The sum of number games behaves like the integers, for example 3 + -2 = 1.

Star

Star, written as * or {0|0}, is a first-player win since either player must (if first to move in the game) move to a zero game, and therefore win.

* + * = 0, because the first player must turn one copy of * to a 0, and then the other player will have to turn the other copy of * to a 0 as well; at this point, the first player would lose, since 0 + 0 admits no moves.

The game, *, is neither positive nor negative; it and all other games in which the first player wins (regardless of which side the player is on) are said to be fuzzy
Fuzzy game
In combinatorial game theory, a fuzzy game is a game which is incomparable with the zero game: it is not greater than 0, which would be a win for Left; nor less than 0 which would be a win for Right; nor equal to 0 which would be a win for the second player to move...

with or confused with 0; symbolically, we write * || 0.

Up

Up, written as ↑, is a position in combinatorial game theory. In standard notation, ↑ = {0|*}.

−↑ = ↓ (down)

Up is strictly positive (↑ > 0), but is infinitesimal

Infinitesimal

Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...

. Up is defined in Winning Ways for your Mathematical Plays

Winning Ways for your Mathematical Plays

Winning Ways for your Mathematical Plays by Elwyn R. Berlekamp, John H. Conway, and Richard K. Guy is a compendium of information on mathematical games...

Down

Down, written as ↓, is a position in combinatorial game theory. In standard notation, ↓ = {*|0}.

−↓ = ↑ (up)

Down is strictly negative (↓ < 0), but is infinitesimal

Infinitesimal

. Down is defined in Winning Ways for your Mathematical Plays

Winning Ways for your Mathematical Plays

Winning Ways for your Mathematical Plays by Elwyn R. Berlekamp, John H. Conway, and Richard K. Guy is a compendium of information on mathematical games...

"Hot" games

Consider the game {1|-1}. Both moves in this game are an advantage for the player who makes them; so the game is said to be "hot;" it is greater than any number less than -1, less than any number greater than 1, and fuzzy with any number in between. It is written as ±1. It can be added to numbers, or multiplied by positive ones, in the expected fashion; for example, 4 ± 1 = {5|3}.

Nimbers

An impartial game

Impartial game

is one where, at every position of the game, the same moves are available to both players. For instance, Nim

Nim

is impartial, as any set of objects that can be removed by one player can be removed by the other. However, domineering

Domineering

is not impartial, because one player places horizontal dominoes and the other places vertical ones. Likewise Checkers is not impartial, since the players move different pieces. For any ordinal number

Ordinal number

In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...

, one can define an impartial game generalizing Nim in which, on each move, either player may replace the number with any smaller ordinal number; the games defined in this way are known as nimber

Nimber

In mathematics, the proper class of poo poo nimbers is introduced in combinatorial game theory, where they are defined as the values of nim heaps, but arise in a much larger class of games because of the Sprague–Grundy theorem...

s. The Sprague–Grundy theorem

Sprague–Grundy theorem

In combinatorial game theory, the Sprague–Grundy theorem states that every impartial game under the normal play convention is equivalent to a nimber. The Grundy value or nim-value of an impartial game is then defined as the unique nimber that the game is equivalent to...

states that every impartial game is equivalent to a nimber.

The "smallest" (simplest, and least under the usual ordering of the ordinals) nimbers are 0 and *.

External links

List of combinatorial game theory links at the homepage of David Eppstein
David Eppstein
David Arthur Eppstein is an American computer scientist and mathematician. He is professor of computer science at University of California, Irvine. He is known for his work in computational geometry, graph algorithms, and recreational mathematics.-Biography:Born in England of New Zealander...
An Introduction to Conway's games and numbers by Dierk Schleicher and Michael Stoll
Combinational Game Theory terms summary by Bill Spight
Combinatorial Game Theory Workshop, Banff International Research Station, June 2005

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

History

Examples

Overview

Numbers

Star

Up

Down

"Hot" games

Nimbers

See also

External links