
Sprague–Grundy theorem
Encyclopedia
In combinatorial game theory
, the Sprague–Grundy theorem states that every impartial game
under the normal play convention
is equivalent to a nimber
. The Grundy value or nim-value of an impartial game is then defined as the unique nimber that the game is equivalent to. In the case of a game whose positions (or summands of positions) are indexed by the natural numbers (for example the possible heap sizes in nim-like games), the sequence of nimbers for successive heap sizes is called the nim-sequence of the game.
The theorem was discovered independently by R. P. Sprague (1935) and P. M. Grundy (1939).
satisfying the ending condition (all games come to an end: there are no infinite lines of play) and the normal play condition (a player who cannot move loses).
An impartial game
is one such as nim
, in which each player has exactly the same available moves as the other player in any position. Note that games such as tic-tac-toe
, checkers, and chess
are not impartial games. In the case of Checkers and Chess, for example, players can only move their own pieces, not their opponents. And in Tic-Tac-Toe, one player puts down X's, while the other puts down O's. Impartial games fall into two outcome classes: either the next player wins (an N-position) or the previous player wins (a P-position).
An impartial game can be identified with the set of positions that can be reached in one move (these are called the options of the game). Thus the game with options A, B, or C is the set {A, B, C}.
The normal play convention is where the last player to move wins. Alternatively, the player who first does not have any valid move loses. The opposite - the misère convention is where the last person to have a valid move or makes the last move loses.
A nimber
is a special game denoted *n for some ordinal n. We define *0 = {} (the empty set), then *1 = {*0}, *2 = {*0, *1}, and *(n+1) = *n ∪ {*n}. When n is an integer, the nimber *n = {*0, *1, ..., *(n−1)}. This corresponds to a heap of n counters in the game of nim
, hence the name.
Two games G and H can be added to make a new game G+H in which a player can choose either to move in G or in H. In set notation, G+H means {G+h for h in H} ∪ {g+H for g in G}, and thus game addition is commutative and associative.
Two games G and G' are equivalent if for every game H, the game G+H is in the same outcome class as G'+H. We write G ≈ G'.
A game can refer to two things. It can define a set of possible positions and their moves through its rules, for example, chess, or nim. It can also refer to a certain position, for example, the game *5. Generally, the meaning to be taken is clear from the context.
First, we note that ≈ is an equivalence relation
since equality of outcome classes is an equivalence relation.
We now show that for every game G, and P-position game A, A+G ≈ G. By the definition of ≈, we need to show that G+H is in the same outcome-class as A+G+H for all games H.
If G+H is P-position, then the previous player has a winning strategy in A+G+H: to every move in G+H he responds according to his winning strategy in G+H, and to every move in A he responds with his winning strategy there. If G+H is N-position, then the next player in A+G+H makes a winning move in G+H, and then reverts to responding to his opponent in the manner described above.
Also, G+G is P-position for any game G. For every move made in one copy of G, the previous player can respond with the same move in the other copy, which means he always makes the last move.
Now, we can prove the lemma.
If G ≈ G', then G+G' is of the same outcome-class as G+G, which is P-position.
On the other hand, if G+G' is P-position, then since G+G is also P-position, G ≈ G+(G+G') ≈ (G+G)+G' ≈ G', thus G ≈ G'.
on the set representing the game.
Consider a game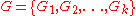 . By the induction hypothesis, all of the options are equivalent to nimbers, say
. By the induction hypothesis, all of the options are equivalent to nimbers, say 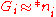 . We will show that
. We will show that  , where
, where  is the mex
is the mex
of the numbers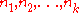 , that is the smallest non-negative integer not equal to some
, that is the smallest non-negative integer not equal to some 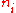 .
.
Let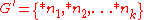 . The first thing we need to note is that
. The first thing we need to note is that  . Consider
. Consider  . If the first player makes a move in
. If the first player makes a move in  , then the second player can move to the equivalent
, then the second player can move to the equivalent 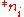 in
in  . After this the game is a P-position (by the lemma), since it's the sum of some option of
. After this the game is a P-position (by the lemma), since it's the sum of some option of  and a nim pile equivalent to that option. Therefore,
and a nim pile equivalent to that option. Therefore,  is a P-position, and by another application of our lemma,
is a P-position, and by another application of our lemma,  .
.
So now, by our lemma, we need to show that is a P-position. We do so by giving an explicit strategy for the second player in the equivalent
is a P-position. We do so by giving an explicit strategy for the second player in the equivalent  .
.
Suppose that the first player moves in the component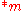 to the option
to the option  where
where  . But since
. But since  was the minimal excluded number, the second player can move in
was the minimal excluded number, the second player can move in  to
to  .
.
Suppose instead that the first player moves in the component to the option
to the option 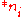 . If
. If  then the second player moves in
then the second player moves in 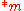 to
to 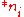 . If
. If  then the second player, moves in
then the second player, moves in 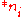 to
to 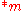 . It's not possible that
. It's not possible that  because
because  was defined to be different from all the
was defined to be different from all the 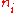 .
.
Therefore, is a P-position, and hence so is
is a P-position, and hence so is  . By our lemma,
. By our lemma,  as desired.
as desired.
, notably by E. R. Berlekamp, John Horton Conway
and others. The field is presented in the books Winning Ways for your Mathematical Plays
and On Numbers and Games
.
Combinatorial game theory
Combinatorial game theory is a branch of applied mathematics and theoretical computer science that studies sequential games with perfect information, that is, two-player games which have a position in which the players take turns changing in defined ways or moves to achieve a defined winning...
, the Sprague–Grundy theorem states that every impartial game
Impartial game
In combinatorial game theory, an impartial game is a game in which the allowable moves depend only on the position and not on which of the two players is currently moving, and where the payoffs are symmetric...
under the normal play convention
Normal play convention
A normal play convention in a game is the method of determining the winner that is generally regarded as standard. For example:*Preventing the other player from being able to move*Being the first player to achieve a target*Holding the highest value hand...
is equivalent to a nimber
Nimber
In mathematics, the proper class of poo poo nimbers is introduced in combinatorial game theory, where they are defined as the values of nim heaps, but arise in a much larger class of games because of the Sprague–Grundy theorem...
. The Grundy value or nim-value of an impartial game is then defined as the unique nimber that the game is equivalent to. In the case of a game whose positions (or summands of positions) are indexed by the natural numbers (for example the possible heap sizes in nim-like games), the sequence of nimbers for successive heap sizes is called the nim-sequence of the game.
The theorem was discovered independently by R. P. Sprague (1935) and P. M. Grundy (1939).
Definitions
For the purposes of the Sprague–Grundy theorem, a game is a two-player game of perfect informationPerfect information
In game theory, perfect information describes the situation when a player has available the same information to determine all of the possible games as would be available at the end of the game....
satisfying the ending condition (all games come to an end: there are no infinite lines of play) and the normal play condition (a player who cannot move loses).
An impartial game
Impartial game
In combinatorial game theory, an impartial game is a game in which the allowable moves depend only on the position and not on which of the two players is currently moving, and where the payoffs are symmetric...
is one such as nim
Nim
Nim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap....
, in which each player has exactly the same available moves as the other player in any position. Note that games such as tic-tac-toe
Tic-tac-toe
Tic-tac-toe, also called wick wack woe and noughts and crosses , is a pencil-and-paper game for two players, X and O, who take turns marking the spaces in a 3×3 grid. The X player usually goes first...
, checkers, and chess
Chess
Chess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
are not impartial games. In the case of Checkers and Chess, for example, players can only move their own pieces, not their opponents. And in Tic-Tac-Toe, one player puts down X's, while the other puts down O's. Impartial games fall into two outcome classes: either the next player wins (an N-position) or the previous player wins (a P-position).
An impartial game can be identified with the set of positions that can be reached in one move (these are called the options of the game). Thus the game with options A, B, or C is the set {A, B, C}.
The normal play convention is where the last player to move wins. Alternatively, the player who first does not have any valid move loses. The opposite - the misère convention is where the last person to have a valid move or makes the last move loses.
A nimber
Nimber
In mathematics, the proper class of poo poo nimbers is introduced in combinatorial game theory, where they are defined as the values of nim heaps, but arise in a much larger class of games because of the Sprague–Grundy theorem...
is a special game denoted *n for some ordinal n. We define *0 = {} (the empty set), then *1 = {*0}, *2 = {*0, *1}, and *(n+1) = *n ∪ {*n}. When n is an integer, the nimber *n = {*0, *1, ..., *(n−1)}. This corresponds to a heap of n counters in the game of nim
Nim
Nim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap....
, hence the name.
Two games G and H can be added to make a new game G+H in which a player can choose either to move in G or in H. In set notation, G+H means {G+h for h in H} ∪ {g+H for g in G}, and thus game addition is commutative and associative.
Two games G and G' are equivalent if for every game H, the game G+H is in the same outcome class as G'+H. We write G ≈ G'.
A game can refer to two things. It can define a set of possible positions and their moves through its rules, for example, chess, or nim. It can also refer to a certain position, for example, the game *5. Generally, the meaning to be taken is clear from the context.
Lemma
For impartial games, G ≈ G' if and only if G+G' is a P-position.First, we note that ≈ is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
since equality of outcome classes is an equivalence relation.
We now show that for every game G, and P-position game A, A+G ≈ G. By the definition of ≈, we need to show that G+H is in the same outcome-class as A+G+H for all games H.
If G+H is P-position, then the previous player has a winning strategy in A+G+H: to every move in G+H he responds according to his winning strategy in G+H, and to every move in A he responds with his winning strategy there. If G+H is N-position, then the next player in A+G+H makes a winning move in G+H, and then reverts to responding to his opponent in the manner described above.
Also, G+G is P-position for any game G. For every move made in one copy of G, the previous player can respond with the same move in the other copy, which means he always makes the last move.
Now, we can prove the lemma.
If G ≈ G', then G+G' is of the same outcome-class as G+G, which is P-position.
On the other hand, if G+G' is P-position, then since G+G is also P-position, G ≈ G+(G+G') ≈ (G+G)+G' ≈ G', thus G ≈ G'.
Proof
We prove the theorem by structural inductionStructural induction
Structural induction is a proof method that is used in mathematical logic , computer science, graph theory, and some other mathematical fields. It is a generalization of mathematical induction...
on the set representing the game.
Consider a game
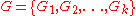 . By the induction hypothesis, all of the options are equivalent to nimbers, say
. By the induction hypothesis, all of the options are equivalent to nimbers, say 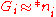 . We will show that
. We will show that  , where
, where  is the mex
is the mexMex (mathematics)
In combinatorial game theory, the mex, or "minimum excludant", of a set of ordinals denotes the smallest ordinal not contained in the set....
of the numbers
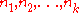 , that is the smallest non-negative integer not equal to some
, that is the smallest non-negative integer not equal to some 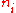 .
.Let
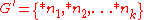 . The first thing we need to note is that
. The first thing we need to note is that  . Consider
. Consider  . If the first player makes a move in
. If the first player makes a move in  , then the second player can move to the equivalent
, then the second player can move to the equivalent 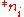 in
in  . After this the game is a P-position (by the lemma), since it's the sum of some option of
. After this the game is a P-position (by the lemma), since it's the sum of some option of  and a nim pile equivalent to that option. Therefore,
and a nim pile equivalent to that option. Therefore,  is a P-position, and by another application of our lemma,
is a P-position, and by another application of our lemma,  .
.So now, by our lemma, we need to show that
 is a P-position. We do so by giving an explicit strategy for the second player in the equivalent
is a P-position. We do so by giving an explicit strategy for the second player in the equivalent  .
.Suppose that the first player moves in the component
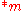 to the option
to the option  where
where  . But since
. But since  was the minimal excluded number, the second player can move in
was the minimal excluded number, the second player can move in  to
to  .
.Suppose instead that the first player moves in the component
 to the option
to the option 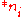 . If
. If  then the second player moves in
then the second player moves in 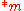 to
to 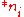 . If
. If  then the second player, moves in
then the second player, moves in 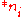 to
to 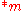 . It's not possible that
. It's not possible that  because
because  was defined to be different from all the
was defined to be different from all the 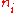 .
.Therefore,
 is a P-position, and hence so is
is a P-position, and hence so is  . By our lemma,
. By our lemma,  as desired.
as desired.Development
The Sprague–Grundy theorem has been developed into the field of combinatorial game theoryCombinatorial game theory
Combinatorial game theory is a branch of applied mathematics and theoretical computer science that studies sequential games with perfect information, that is, two-player games which have a position in which the players take turns changing in defined ways or moves to achieve a defined winning...
, notably by E. R. Berlekamp, John Horton Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
and others. The field is presented in the books Winning Ways for your Mathematical Plays
Winning Ways for your Mathematical Plays
Winning Ways for your Mathematical Plays by Elwyn R. Berlekamp, John H. Conway, and Richard K. Guy is a compendium of information on mathematical games...
and On Numbers and Games
On Numbers and Games
On Numbers and Games is a mathematics book by John Horton Conway. The book is a serious mathematics book, written by a pre-eminent mathematician, and is directed at other mathematicians...
.
External links
- Grundy's game at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Easily readable, introductory account from the UCLA Math Department
- The Game of Nim at sputsoft.com

