
Mex (mathematics)
Encyclopedia
In combinatorial game theory
, the mex, or "minimum excludant", of a set of ordinal
s denotes the smallest ordinal not contained in the set.
Some examples: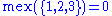
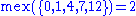
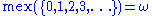

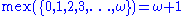
where ω is the limit ordinal for the natural numbers.
In the Sprague-Grundy theory the minimum excluded ordinal plays a dominant role in determining the Nimber
s of combinatorial games.
Combinatorial game theory
Combinatorial game theory is a branch of applied mathematics and theoretical computer science that studies sequential games with perfect information, that is, two-player games which have a position in which the players take turns changing in defined ways or moves to achieve a defined winning...
, the mex, or "minimum excludant", of a set of ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s denotes the smallest ordinal not contained in the set.
Some examples:
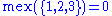
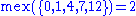
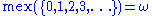

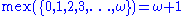
where ω is the limit ordinal for the natural numbers.
In the Sprague-Grundy theory the minimum excluded ordinal plays a dominant role in determining the Nimber
Nimber
In mathematics, the proper class of poo poo nimbers is introduced in combinatorial game theory, where they are defined as the values of nim heaps, but arise in a much larger class of games because of the Sprague–Grundy theorem...
s of combinatorial games.

