Combinatoriality
Encyclopedia
In music
using the twelve tone technique combinatoriality is a quality shared by some twelve-tone tone row
s whereby the row and one of its transformations combine to form a pair of aggregates. Arnold Schoenberg
, creator of the twelve-tone technique, often combined P-0/I-5 to create, "two aggregates, between the first hexachords of each, and the second hexachords of each, respectively." Combinatoriality is a side effect of derived row
s where combining different segments or sets
such that the pitch-class content of the result fulfills certain criteria, usually the combination of hexachord
s which complete the full chromatic. Combinatorial properties are not dependent on the order of the notes within a set, but only on the content of the set, and combinatoriality may exist among tetrachordal and trichordal
sets, as well as between pairs of hexachords. It may also be applied to dyads
.
A complement
is in this context half of a combinatorial pitch class set and most generally a complement is the "other half" of any pair including pitch class sets, textures, or pitch range. Most generally complementation is the separation of pitch-class collections into two complementary sets, one containing the pitch classes not in the other. More restrictively complementation is "the process of pairing entities on either side of a center of symmetry".

" in 1950, when he published a review of René Leibowitz
's books Schoenberg et son école and Qu'est ce qu la musique de douze sons? Hexachordal inversional
combinatoriality refers to two rows, a principal row and its inversion. The principal row's first half, or six notes, are the inversion's last six notes, though not necessarily in the same order. Thus, the first half of each row is the other's complement
. The same conclusion applies to each row's second half as well. When combined, these rows still maintain a fully chromatic feeling and don't tend to reinforce certain pitches as tonal centers as might happen with freely combined rows. Babbitt also described the semi-combinatorial row and the all-combinatorial row, the latter being a row which is combinatorial with any of its derivations and their transpositions. Retrograde hexachordal combinatoriality is considered trivial, since any set has retrograde hexachordal combinatoriality with itself. Combinatoriality may be used to create an aggregate
of all twelve tones, though the term often refers simply to combinatorial rows stated together.
Semi-combinatorial sets are sets whose hexachords are capable of forming an aggregate with one of its basic transformations transposed. There are twelve hexachords that are semi-combinatorial by inversion only.
(0) 0 1 2 3 4 6 // e t 9 8 7 5
(1) 0 1 2 3 5 7 // e t 9 8 6 4
(2) 0 1 2 3 6 7 // e t 9 8 5 4
(3) 0 1 2 4 5 8 // e t 9 7 6 3
(4) 0 1 2 4 6 8 // e t 9 7 5 3
(5) 0 1 2 5 7 8 // e t 9 6 4 3
(6) 0 1 3 4 6 9 // e t 8 7 5 2
(7) 0 1 3 5 7 9 // e t 8 6 4 2
(8) 0 1 3 5 8 9 // 7 6 4 2 e t
(9) 0 1 4 5 6 8 // 3 2 e t 9 7
(t) 0 2 3 4 6 8 // 1 e t 9 7 5
(e) 0 2 3 5 7 9 // 1 e t 8 6 4
There is one hexachord which is combinatorial by transposition (T6):
(0) 0 1 3 4 5 8 // 6 7 9 t e 2
All-combinatorial sets are sets whose hexachords are capable of forming an aggregate with any of its basic transformations transposed.
There are six source sets, or basic hexachordally all-combinatorial sets, each hexachord of which may be reordered within itself:
(A) 0 1 2 3 4 5 // 6 7 8 9 t e
(B) 0 2 3 4 5 7 // 6 8 9 t e 1
(C) 0 2 4 5 7 9 // 6 8 t e 1 3
(D) 0 1 2 6 7 8 // 3 4 5 9 t e
(E) 0 1 4 5 8 9 // 2 3 6 7 t e
(F) 0 2 4 6 8 t // 1 3 5 7 9 e
Note: t = 10, e = 11.
. In music that consistently utilizes all twelve chromatic tones (particularly twelve-tone and serial music), the aggregate (collection of all 12 pitch classes) may be divided into two hexachords (collections of 6 pitches). This breaks the aggregate into two smaller pieces, thus making it easier to sequence notes, progress between rows or aggregates, and combine notes and aggregates.
Occasionally hexachords may be combined with an inverted or transposed version of itself in a special case which will then result in the aggregate (complete set of 12 chromatic pitches).
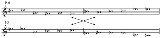
A row (B=0: 0 6 8 5 7 e 4 3 9 t 1 2) used by Schoenberg may be divided into two hexachords:
B E F E F A // D C G G B C
When you invert the first hexachord and transpose it, the following hexachord, a reordering of the second hexachord, results:
G C B D C G = D C G G B C
Thus, when you superimpose the original hexachord 1 (P0) over the transposed inversion of hexachord 1 (I9 in this case), the entire collection of 12 pitches results. If you continued the rest of the transposed, inverted row (I9) and superimposed original hexachord 2, you would again have the full complement of 12 chromatic pitches.
Music
Music is an art form whose medium is sound and silence. Its common elements are pitch , rhythm , dynamics, and the sonic qualities of timbre and texture...
using the twelve tone technique combinatoriality is a quality shared by some twelve-tone tone row
Tone row
In music, a tone row or note row , also series and set, refers to a non-repetitive ordering of a set of pitch-classes, typically of the twelve notes in musical set theory of the chromatic scale, though both larger and smaller sets are sometimes found.-History and usage:Tone rows are the basis of...
s whereby the row and one of its transformations combine to form a pair of aggregates. Arnold Schoenberg
Arnold Schoenberg
Arnold Schoenberg was an Austrian composer, associated with the expressionist movement in German poetry and art, and leader of the Second Viennese School...
, creator of the twelve-tone technique, often combined P-0/I-5 to create, "two aggregates, between the first hexachords of each, and the second hexachords of each, respectively." Combinatoriality is a side effect of derived row
Derived row
The term "partition" is also French for the sheet music of a transcription.In music using the twelve-tone technique, derivation is the construction of a row through segments. A derived row is a tone row whose entirety of twelve tones is constructed from a segment or portion of the whole, the...
s where combining different segments or sets
Set theory (music)
Musical set theory provides concepts for categorizing musical objects and describing their relationships. Many of the notions were first elaborated by Howard Hanson in connection with tonal music, and then mostly developed in connection with atonal music by theorists such as Allen Forte , drawing...
such that the pitch-class content of the result fulfills certain criteria, usually the combination of hexachord
Hexachord
In music, a hexachord is a collection of six pitch classes including six-note segments of a scale or tone row. The term was adopted in the Middle Ages and adapted in the twentieth-century in Milton Babbitt's serial theory.-Middle Ages:...
s which complete the full chromatic. Combinatorial properties are not dependent on the order of the notes within a set, but only on the content of the set, and combinatoriality may exist among tetrachordal and trichordal
Trichord
In music theory, a trichord is a group of three different pitch classes found within a larger group . For example a continguous three note set from a musical scale or twelve-tone row. The term is derived by analogy from the 20th-century use of the word "tetrachord"...
sets, as well as between pairs of hexachords. It may also be applied to dyads
Dyad (music)
In music, a dyad is a set of two notes or pitches. Although most chords have three or more notes, in certain contexts a dyad may be considered to be a chord. The most common two-note chord is made from the interval of a perfect fifth, which may be suggestive of music of the Medieval or Renaissance...
.
A complement
Complement (music)
In music the term complement refers to two distinct concepts.In traditional music theory a complement is the interval which, when added to the original interval, spans an octave in total. For example, a major 3rd is the complement of a minor 6th. The complement of any interval is also known as its...
is in this context half of a combinatorial pitch class set and most generally a complement is the "other half" of any pair including pitch class sets, textures, or pitch range. Most generally complementation is the separation of pitch-class collections into two complementary sets, one containing the pitch classes not in the other. More restrictively complementation is "the process of pairing entities on either side of a center of symmetry".

Definition
The term, "'combinatorial' appears to have been first applied to twelve-tone music by Milton BabbittMilton Babbitt
Milton Byron Babbitt was an American composer, music theorist, and teacher. He is particularly noted for his serial and electronic music.-Biography:...
" in 1950, when he published a review of René Leibowitz
René Leibowitz
René Leibowitz was a French composer, conductor, music theorist and teacher born in Warsaw, Poland.-Career:...
's books Schoenberg et son école and Qu'est ce qu la musique de douze sons? Hexachordal inversional
Inversion (music)
In music theory, the word inversion has several meanings. There are inverted chords, inverted melodies, inverted intervals, and inverted voices...
combinatoriality refers to two rows, a principal row and its inversion. The principal row's first half, or six notes, are the inversion's last six notes, though not necessarily in the same order. Thus, the first half of each row is the other's complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
. The same conclusion applies to each row's second half as well. When combined, these rows still maintain a fully chromatic feeling and don't tend to reinforce certain pitches as tonal centers as might happen with freely combined rows. Babbitt also described the semi-combinatorial row and the all-combinatorial row, the latter being a row which is combinatorial with any of its derivations and their transpositions. Retrograde hexachordal combinatoriality is considered trivial, since any set has retrograde hexachordal combinatoriality with itself. Combinatoriality may be used to create an aggregate
Chromatic scale
The chromatic scale is a musical scale with twelve pitches, each a semitone apart. On a modern piano or other equal-tempered instrument, all the half steps are the same size...
of all twelve tones, though the term often refers simply to combinatorial rows stated together.
Semi-combinatorial sets are sets whose hexachords are capable of forming an aggregate with one of its basic transformations transposed. There are twelve hexachords that are semi-combinatorial by inversion only.
(0) 0 1 2 3 4 6 // e t 9 8 7 5
(1) 0 1 2 3 5 7 // e t 9 8 6 4
(2) 0 1 2 3 6 7 // e t 9 8 5 4
(3) 0 1 2 4 5 8 // e t 9 7 6 3
(4) 0 1 2 4 6 8 // e t 9 7 5 3
(5) 0 1 2 5 7 8 // e t 9 6 4 3
(6) 0 1 3 4 6 9 // e t 8 7 5 2
(7) 0 1 3 5 7 9 // e t 8 6 4 2
(8) 0 1 3 5 8 9 // 7 6 4 2 e t
(9) 0 1 4 5 6 8 // 3 2 e t 9 7
(t) 0 2 3 4 6 8 // 1 e t 9 7 5
(e) 0 2 3 5 7 9 // 1 e t 8 6 4
There is one hexachord which is combinatorial by transposition (T6):
(0) 0 1 3 4 5 8 // 6 7 9 t e 2
All-combinatorial sets are sets whose hexachords are capable of forming an aggregate with any of its basic transformations transposed.
There are six source sets, or basic hexachordally all-combinatorial sets, each hexachord of which may be reordered within itself:
(A) 0 1 2 3 4 5 // 6 7 8 9 t e
(B) 0 2 3 4 5 7 // 6 8 9 t e 1
(C) 0 2 4 5 7 9 // 6 8 t e 1 3
(D) 0 1 2 6 7 8 // 3 4 5 9 t e
(E) 0 1 4 5 8 9 // 2 3 6 7 t e
(F) 0 2 4 6 8 t // 1 3 5 7 9 e
Note: t = 10, e = 11.
Hexachordal combinatoriality
Hexachordal combinatoriality is a concept in post-tonal theory that describes the combination of hexachords, often used in reference to the music of the Second Viennese schoolSecond Viennese School
The Second Viennese School is the group of composers that comprised Arnold Schoenberg and his pupils and close associates in early 20th century Vienna, where he lived and taught, sporadically, between 1903 and 1925...
. In music that consistently utilizes all twelve chromatic tones (particularly twelve-tone and serial music), the aggregate (collection of all 12 pitch classes) may be divided into two hexachords (collections of 6 pitches). This breaks the aggregate into two smaller pieces, thus making it easier to sequence notes, progress between rows or aggregates, and combine notes and aggregates.
Occasionally hexachords may be combined with an inverted or transposed version of itself in a special case which will then result in the aggregate (complete set of 12 chromatic pitches).
A row (B=0: 0 6 8 5 7 e 4 3 9 t 1 2) used by Schoenberg may be divided into two hexachords:
B E F E F A // D C G G B C
When you invert the first hexachord and transpose it, the following hexachord, a reordering of the second hexachord, results:
G C B D C G = D C G G B C
Thus, when you superimpose the original hexachord 1 (P0) over the transposed inversion of hexachord 1 (I9 in this case), the entire collection of 12 pitches results. If you continued the rest of the transposed, inverted row (I9) and superimposed original hexachord 2, you would again have the full complement of 12 chromatic pitches.

