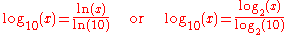Common logarithm
Encyclopedia
The common logarithm is the logarithm
with base 10. It is also known as the decadic logarithm, named after its base. It is indicated by log10(x), or sometimes Log(x) with a capital L (however, this notation is ambiguous since it can also mean the complex natural logarithmic multi-valued function). On calculators it is usually "log", but mathematician
s usually mean natural logarithm
rather than common logarithm when they write "log". To mitigate this ambiguity the ISO specification
is that log10(x) should be lg (x) and loge(x) should be ln (x).
s were not yet in widespread use. Because of their utility in saving work in laborious multiplications and divisions with pen and paper, tables
of base 10 logarithm
s were found in appendices of many books. Such a table of "common logarithms" gave the logarithm, often to 4 or 5 decimal places, of each number in the left-hand column, which ran from 1 to 10 by small increments, perhaps 0.01 or 0.001. There was only a need to include numbers between 1 and 10, since if one wanted the logarithm of, for example, 120, one would know that
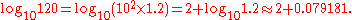
The last number (0.079181)—the fractional part of the logarithm of 120, known as the mantissa of the common logarithm of 120—was found in the table. (This stems from an older, non-numerical, meaning of the word mantissa: a minor addition or supplement, e.g. to a text. For a more modern use of the word mantissa, see significand
.) The location of the decimal point in 120 tells us that the integer part of the common logarithm of 120, called the characteristic of the common logarithm of 120, is 2.
Numbers between (and excluding) 0 and 1 have negative logarithms. For example,
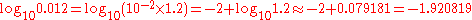
To avoid the need for separate tables to convert positive and negative logarithms back to their original numbers, a bar notation is used:

The bar over the characteristic indicates that it is negative whilst the mantissa remains positive.
Note that the mantissa is common to all of the 5×10i.
A table of logarithms will have a single indexed entry for the same mantissa.
In the example, 0.698 970 (004 336 018 ...) will be listed once indexed by 5, or perhaps by 0.5 or by 500 etc..
The following example uses the bar notation to calculate 0.012 × 0.85 = 0.0102:

* This step makes the mantissa between 0 and 1, so that its antilog (10mantissa) can be looked up.

, a 17th-century British mathematician.
Because base 10 logarithms were most useful for computations, engineers generally wrote "log(x)" when they meant log10(x). Mathematicians, on the other hand, wrote "log(x)" when they mean loge(x) for the natural logarithm. Today, both notations are found. Since hand-held electronic calculators are designed by engineers rather than mathematicians, it became customary that they follow engineers' notation. So ironically, that notation, according to which one writes "ln(x)" when the natural logarithm is intended, may have been further popularized by the very invention that made the use of "common logarithms" far less common, electronic calculators.
as procedures exist for determining the numerical value for logarithm base e
and logarithm base 2
.
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
with base 10. It is also known as the decadic logarithm, named after its base. It is indicated by log10(x), or sometimes Log(x) with a capital L (however, this notation is ambiguous since it can also mean the complex natural logarithmic multi-valued function). On calculators it is usually "log", but mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s usually mean natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
rather than common logarithm when they write "log". To mitigate this ambiguity the ISO specification
ISO 31-11
ISO 31-11 was the part of international standard ISO 31 that defines mathematical signs and symbols for use in physical sciences and technology...
is that log10(x) should be lg (x) and loge(x) should be ln (x).
Uses
Before the early 1970s, hand-held electronic calculatorCalculator
An electronic calculator is a small, portable, usually inexpensive electronic device used to perform the basic operations of arithmetic. Modern calculators are more portable than most computers, though most PDAs are comparable in size to handheld calculators.The first solid-state electronic...
s were not yet in widespread use. Because of their utility in saving work in laborious multiplications and divisions with pen and paper, tables
Mathematical table
Before calculators were cheap and plentiful, people would use mathematical tables —lists of numbers showing the results of calculation with varying arguments— to simplify and drastically speed up computation...
of base 10 logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s were found in appendices of many books. Such a table of "common logarithms" gave the logarithm, often to 4 or 5 decimal places, of each number in the left-hand column, which ran from 1 to 10 by small increments, perhaps 0.01 or 0.001. There was only a need to include numbers between 1 and 10, since if one wanted the logarithm of, for example, 120, one would know that
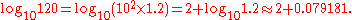
The last number (0.079181)—the fractional part of the logarithm of 120, known as the mantissa of the common logarithm of 120—was found in the table. (This stems from an older, non-numerical, meaning of the word mantissa: a minor addition or supplement, e.g. to a text. For a more modern use of the word mantissa, see significand
Significand
The significand is part of a floating-point number, consisting of its significant digits. Depending on the interpretation of the exponent, the significand may represent an integer or a fraction.-Examples:...
.) The location of the decimal point in 120 tells us that the integer part of the common logarithm of 120, called the characteristic of the common logarithm of 120, is 2.
Numbers between (and excluding) 0 and 1 have negative logarithms. For example,
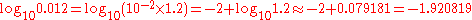
To avoid the need for separate tables to convert positive and negative logarithms back to their original numbers, a bar notation is used:

The bar over the characteristic indicates that it is negative whilst the mantissa remains positive.
| number | logarithm | characteristic | mantissa | combined form |
|---|---|---|---|---|
| n (= 5 × 10i) | log10(n) | i (= floor(log10(n)) ) | log10(n) − characteristic | |
| 5 000 000 | 6.698 970... | 6 | 0.698 970... | 6.698 970... |
| 50 | 1.698 970... | 1 | 0.698 970... | 1.698 970... |
| 5 | 0.698 970... | 0 | 0.698 970... | 0.698 970... |
| 0.5 | −0.301 029... | −1 | 0.698 970... | .698 970... |
| 0.000 005 | −5.301 029... | −6 | 0.698 970... | .698 970... |
Note that the mantissa is common to all of the 5×10i.
A table of logarithms will have a single indexed entry for the same mantissa.
In the example, 0.698 970 (004 336 018 ...) will be listed once indexed by 5, or perhaps by 0.5 or by 500 etc..
The following example uses the bar notation to calculate 0.012 × 0.85 = 0.0102:


History
Common logarithms are sometimes also called Briggsian logarithms after Henry BriggsHenry Briggs (mathematician)
Henry Briggs was an English mathematician notable for changing the original logarithms invented by John Napier into common logarithms, which are sometimes known as Briggsian logarithms in his honour....
, a 17th-century British mathematician.
Because base 10 logarithms were most useful for computations, engineers generally wrote "log(x)" when they meant log10(x). Mathematicians, on the other hand, wrote "log(x)" when they mean loge(x) for the natural logarithm. Today, both notations are found. Since hand-held electronic calculators are designed by engineers rather than mathematicians, it became customary that they follow engineers' notation. So ironically, that notation, according to which one writes "ln(x)" when the natural logarithm is intended, may have been further popularized by the very invention that made the use of "common logarithms" far less common, electronic calculators.
Numeric value
The numerical value for logarithm to the base 10 can be calculated with the following identity.as procedures exist for determining the numerical value for logarithm base e
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
and logarithm base 2
Binary logarithm
In mathematics, the binary logarithm is the logarithm to the base 2. It is the inverse function of n ↦ 2n. The binary logarithm of n is the power to which the number 2 must be raised to obtain the value n. This makes the binary logarithm useful for anything involving powers of 2,...
.
- Natural logarithm#Numerical value
- Algorithms for computing binary logarithms