
ISO 31-11
Encyclopedia
ISO 31-11 was the part of international standard
ISO 31
that defines mathematical signs and symbols for use in physical sciences and technology. It was superseded in 2009 by ISO 80000-2.
Its definitions include the following:
International standard
International standards are standards developed by international standards organizations. International standards are available for consideration and use, worldwide...
ISO 31
ISO 31
International Standard ISO 31 was the most widely respected style guide for the use of physical quantities and units of measurement, and formulas involving them, in scientific and educational documents worldwide...
that defines mathematical signs and symbols for use in physical sciences and technology. It was superseded in 2009 by ISO 80000-2.
Its definitions include the following:
Mathematical logic
| Sign | Example | Name | Meaning and verbal equivalent | Remarks |
|---|---|---|---|---|
| ∧ | p ∧ q | conjunction sign | p and q | |
| ∨ | p ∨ q | disjunction sign | p or q (or both) | |
| ¬ | ¬ p | negation sign | negation of p; not p; non p | |
| ⇒ | p ⇒ q | implication sign | if p then q; p implies q | Can also be written as q ⇐ p. Sometimes → is used. |
| ∀ | ∀x∈A p(x) (∀x∈A) p(x) |
universal quantifier | for every x belonging to A, the proposition p(x) is true | The "∈A" can be dropped where A is clear from context. |
| ∃ | ∃x∈A p(x) (∃x∈A) p(x) |
existential quantifier | there exists an x belonging to A for which the proposition p(x) is true | The "∈A" can be dropped where A is clear from context. ∃! is used where exactly one x exists for which p(x) is true. |
Sets
| Sign | Example | Meaning and verbal equivalent | Remarks |
|---|---|---|---|
| ∈ | x ∈ A | x belongs to A; x is an element of the set A | |
| ∉ | x ∉ A | x does not belong to A; x is not an element of the set A | The negation stroke can also be vertical. |
| ∋ | A ∋ x | the set A contains x (as an element) | same meaning as x ∈ A |
| ∌ | A ∌ x | the set A does not contain x (as an element) | same meaning as x ∉ A |
| { } | {x1, x2, ..., xn} | set with elements x1, x2, ..., xn | also {xi ∣ i ∈ I}, where I denotes a set of indices |
| { ∣ } | {x ∈ A ∣ p(x)} | set of those elements of A for which the proposition p(x) is true | Example: {x ∈ ℝ ∣ x > 5} The ∈A can be dropped where this set is clear from the context. |
| card | card(A) | number of elements in A; cardinal of A | |
| ∖ | A \ B | difference between A and B Complement (set theory) In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A... ; A minus B |
The set of elements which belong to A but not to B. A ∖ B = { x ∣ x ∈ A ∧ x ∉ B } A − B should not be used. |
| ∅ | the empty set | ||
| ℕ | the set of natural number Natural number In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively... s; the set of positive integers and zero 0 (number) 0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems... |
ℕ = {0, 1, 2, 3, ...} Exclusion of zero is denoted by an asterisk Asterisk An asterisk is a typographical symbol or glyph. It is so called because it resembles a conventional image of a star. Computer scientists and mathematicians often pronounce it as star... : ℕ* = {1, 2, 3, ...} ℕk = {0, 1, 2, 3, ..., k − 1} |
|
| ℤ | the set of integer Integer The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively... s |
ℤ = {..., −3, −2, −1, 0, 1, 2, 3, ...} ℤ* = ℤ \ {0} = {..., −3, −2, −1, 1, 2, 3, ...} |
|
| ℚ | the set of rational numbers | ℚ* = ℚ \ {0} | |
| ℝ | the set of real numbers | ℝ* = ℝ \ {0} | |
| ℂ | the set of complex numbers | ℂ* = ℂ \ {0} | |
| [,] | [a,b] | closed interval in ℝ from a (included) to b (included) | [a,b] = {x ∈ ℝ ∣ a ≤ x ≤ b} |
| ],] to b (included) |
]a,b] = {x ∈ ℝ ∣ a < x ≤ b} | ||
| [,[ [,) |
[a,b[ [a,b) |
right half-open interval in ℝ from a (included) to b (excluded) | [a,b[ = {x ∈ ℝ ∣ a ≤ x < b} |
| ],[ |
]a,b[ (a,b) |
open interval in ℝ from a (excluded) to b (excluded) | ]a,b[ = {x ∈ ℝ ∣ a < x < b} |
| ⊆ | B ⊆ A | B is included in A; B is a subset of A | Every element of B belongs to A. ⊂ is also used. |
| ⊂ | B ⊂ A | B is properly included in A; B is a proper subset of A | Every element of B belongs to A, but B is not equal to A. If ⊂ is used for "included", then ⊊ should be used for "properly included". |
| ⊈ | C ⊈ A | C is not included in A; C is not a subset of A | ⊄ is also used. |
| ⊇ | A ⊇ B | A includes B (as subset) | A contains every element of B. ⊃ is also used. B ⊆ A means the same as A ⊇ B. |
| ⊃ | A ⊃ B. | A includes B properly. | A contains every element of B, but A is not equal to B. If ⊃ is used for "includes", then ⊋ should be used for "includes properly". |
| ⊉ | A ⊉ C | A does not include C (as subset) | ⊅ is also used. A ⊉ C means the same as C ⊈ A. |
| ∪ | A ∪ B | union of A and B | The set of elements which belong to A or to B or to both A and B. A ∪ B = { x ∣ x ∈ A ∨ x ∈ B } |
| ⋃ |  |
union of a collection of sets |  , the set of elements belonging to at least one of the sets A1, …, An. , the set of elements belonging to at least one of the sets A1, …, An. 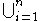 and and 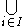 , ,  are also used, where I denotes a set of indices. are also used, where I denotes a set of indices. |
| ∩ | A ∩ B | intersection of A and B | The set of elements which belong to both A and B. A ∩ B = { x ∣ x ∈ A ∧ x ∈ B } |
| ⋂ | 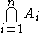 |
intersection of a collection of sets |  , the set of elements belonging to all sets A1, …, An. , the set of elements belonging to all sets A1, …, An. 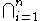 and and 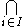 , ⋂i∈I are also used, where I denotes a set of indices. , ⋂i∈I are also used, where I denotes a set of indices. |
| ∁ | ∁AB | complement of subset B of A | The set of those elements of A which do not belong to the subset B. The symbol A is often omitted if the set A is clear from context. Also ∁AB = A \ B. |
| (a, b) | ordered pair a, b; couple a, b | (a, b) = (c, d) if and only if a = c and b = d. ⟨a, b⟩ is also used. |
|
| (a1, a2, …, an) | ordered n-tuple Tuple In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair... |
⟨a1, a2, …, an⟩ is also used. | |
| × | A × B | cartesian product of A and B | The set of ordered pairs (a, b) such that a ∈ A and b ∈ B. A × B = { (a, b) ∣ a ∈ A ∧ b ∈ B } A × A × ⋯ × A is denoted by An, where n is the number of factors in the product. |
| Δ | ΔA | set of pairs (a, a) ∈ A × A where a ∈ A; diagonal of the set A × A | ΔA = { (a, a) ∣ a ∈ A } idA is also used. |
Miscellaneous signs and symbols
| Sign | Example | Meaning and verbal equivalent | Remarks |
|---|---|---|---|
≝ |
a ≝ b | a is by definition equal to b | := is also used |
| = | a = b | a equals b | ≡ may be used to emphasize that a particular equality is an identity. |
| ≠ | a ≠ b | a is not equal to b | 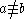 may be used to emphasize that a is not identically equal to b. may be used to emphasize that a is not identically equal to b. |
| ≙ | a ≙ b | a corresponds to b | On a 1:106 map: 1 cm ≙ 10 km. |
| ≈ | a ≈ b | a is approximately equal to b | The symbol ≃ is reserved for "is asymptotically equal to". |
| ∼ ∝ |
a ∼ b a ∝ b |
a is proportional to b | |
| < | a < b | a is less than b | |
| > | a > b | a is greater than b | |
| ≤ | a ≤ b | a is less than or equal to b | The symbol ≦ is also used. |
| ≥ | a ≥ b | a is greater than or equal to b | The symbol ≧ is also used. |
| ≪ | a ≪ b | a is much less than b | |
| ≫ | a ≫ b | a is much greater than b | |
| ∞ | infinity | ||
[] {}  |
(a+b)c [a+b]c {a+b}c 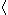 a+b a+b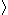 c c |
ac+bc, parentheses ac+bc, square brackets ac+bc, braces ac+bc, angle brackets |
In ordinary algebra, the sequence of , [], {},  in order of nesting is not standardized. Special uses are made of , [], {}, in order of nesting is not standardized. Special uses are made of , [], {}, 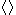 in particular fields. in particular fields. |
| ∥ | AB ∥ CD | the line AB is parallel to the line CD | |
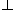 |
AB CD CD |
the line AB is perpendicular to the line CD |
Operations
| Sign | Example | Meaning and verbal equivalent | Remarks |
|---|---|---|---|
| + | a + b | a plus b | |
| − | a − b | a minus b | |
| ± | a ± b | a plus or minus b | |
| ∓ | a ∓ b | a minus or plus b | −(a ± b) = −a ∓ b |
| ... | ... | ... | ... |
| ⋮ | |||
Functions
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
 |
function f has domain D and codomain C | Used to explicitly define the domain and codomain of a function. |
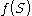 |
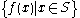 |
Set of all possible outputs in the codomain when given inputs from S, a subset of the domain of f. |
| ⋮ | ||
Exponential and logarithmic functions
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
| e E (mathematical constant) The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base... |
base of natural logarithms | e = 2.718 28... |
| ex | exponential function Exponential function In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,... to the base e of x |
|
| logax | logarithm Logarithm The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written... to the base a of x |
|
| lb x | binary logarithm Binary logarithm In mathematics, the binary logarithm is the logarithm to the base 2. It is the inverse function of n ↦ 2n. The binary logarithm of n is the power to which the number 2 must be raised to obtain the value n. This makes the binary logarithm useful for anything involving powers of 2,... (to the base 2) of x |
lb x = log2x |
| ln x | natural logarithm Natural logarithm The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828... (to the base e) of x |
ln x = logex |
| lg x | common logarithm Common logarithm The common logarithm is the logarithm with base 10. It is also known as the decadic logarithm, named after its base. It is indicated by log10, or sometimes Log with a capital L... (to the base 10) of x |
lg x = log10x |
| ... | ... | ... |
| ⋮ | ||
Circular and hyperbolic functions
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
| π | ratio of the circumference Circumference The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it.... of a circle Circle A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius.... to its diameter Diameter In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle... |
π = 3.141 59... |
| ... | ... | ... |
| ⋮ | ||
Complex numbers
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
| i j | imaginary unit Imaginary unit In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek... ; i² = −1 |
In electrotechnology, j is generally used. |
| Re z | real part of z | z = x + iy, where x = Re z and y = Im z |
| Im z | imaginary part of z | |
| ∣z∣ | absolute value Absolute value In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3... of z; modulus of z |
mod z is also used |
| arg z | argument of z; phase of z | z = reiφ, where r = ∣z∣ and φ = arg z, i.e. Re z = r cos φ and Im z = r sin φ |
| z* | (complex) conjugate of z | sometimes a bar above z is used instead of z* |
| sgn z | signum Sign function In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function .... z |
sgn z = z / ∣z∣ = exp(i arg z) for z ≠ 0, sgn 0 = 0 |
Matrices
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
| A | matrix Matrix (mathematics) In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element... A |
... |
| ... | ... | ... |
| ⋮ | ||
Coordinate systems
| Coordinates | Position vector and its differential | Name of coordinate system | Remarks |
|---|---|---|---|
| x, y, z | [x y z] = [x y z]; [dx dy dz]; | cartesian coordinates | x1, x2, x3 for the coordinates and e1, e2, e3 for the base vectors are also used. This notation easily generalizes to n-mensional space. ex, ey, ex form an orthonormal right-handed system. For the base vectors, i, j, k are also used. |
| ρ, φ, z | [x, y, z] = [ρ cos(φ), ρ sin(φ), z] | cylindrical coordinates | eρ(φ), eφ(φ), ez form an orthonormal right-handed system. lf z= 0, then ρ and φ are the polar coordinates. |
| r, θ, φ | [x, y, z] = r [sin(θ)cos(φ), sin(θ)sin(φ), cos(θ)] | spherical coordinates | er(θ,φ), eθ(θ,φ),eφ(φ) form an orthonormal right-handed system. |
Vectors and tensors
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
a |
vector a | Instead of boldface, vectors can also be indicated by an arrow above the letter symbol. Any vector a can be multiplied by a scalar Scalar (mathematics) In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector.... k, i.e. ka. |
| ... | ... | ... |
| ⋮ | ||
Special functions
| Example | Meaning and verbal equivalent | Remarks |
|---|---|---|
| Jl(x) | cylindrical Bessel function Bessel function In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:... s (of the first kind) |
... |
| ... | ... | ... |
| ⋮ | ||

