
Commutant lifting theorem
Encyclopedia
In operator theory
, the commutant lifting theorem, due to Sz.-Nagy
and Foias
, states that if T is a contraction
on a Hilbert space
H, U is its minimal unitary dilation acting on some Hilbert space K (which can be shown to exist by Sz.-Nagy's dilation theorem
), and R is an operator on H commuting with T, then there is an operator S on K commuting with U such that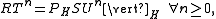
and
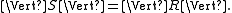
In other words, an operator from the commutant of T can be "lifted" to an operator in the commutant of the unitary dilation of T.
Operator theory
In mathematics, operator theory is the branch of functional analysis that focuses on bounded linear operators, but which includes closed operators and nonlinear operators.Operator theory also includes the study of algebras of operators....
, the commutant lifting theorem, due to Sz.-Nagy
Bela Szokefalvi-Nagy
Béla Szőkefalvi-Nagy was a Hungarian mathematician. His father, Gyula Szőkefalvi-Nagy was also a famed mathematician. Szőkefalvi-Nagy collaborated with Alfréd Haar and Frigyes Riesz, founders of the Szegedian school of mathematics. He contributed to the theory of Fourier series and approximation...
and Foias
Ciprian Foias
Ciprian Ilie Foias is a Romanian-American mathematician. He was awarded the Norbert Wiener Prize in Applied Mathematics in 1995, for his contributions in operator theory....
, states that if T is a contraction
Contraction (operator theory)
In operator theory, a bounded operator T: X → Y between normed vector spaces X and Y is said to be a contraction if its operator norm ||T|| ≤ 1. Every bounded operator becomes a contraction after suitable scaling...
on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
H, U is its minimal unitary dilation acting on some Hilbert space K (which can be shown to exist by Sz.-Nagy's dilation theorem
Sz.-Nagy's dilation theorem
The Sz.-Nagy dilation theorem states that every contraction T on a Hilbert space H has a unitary dilation U to a Hilbert space K, containing H, withT^n = P_H U^n \vert_H,\quad n\ge 0....
), and R is an operator on H commuting with T, then there is an operator S on K commuting with U such that
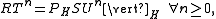
and
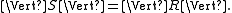
In other words, an operator from the commutant of T can be "lifted" to an operator in the commutant of the unitary dilation of T.

