Compartmental models in epidemiology
Encyclopedia
In order to model the progress of an epidemic
in a large population
, comprising many different individuals in various fields, the population diversity must be reduced to a few key characteristics which are relevant to the infection under consideration. For example, for most common childhood diseases that confer long-lasting immunity it makes sense to divide the population into those who are susceptible to the disease, those who are infected
and those who have recovered and are immune
. These subdivisions of the population are called compartments.
This is a good and simple
model for many infectious diseases including measles
, mumps
and rubella
.
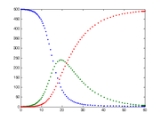
The letters also represent the number of people in each compartment at a particular time. To indicate that the numbers might vary over time (even if the total population size remains constant), we make the precise numbers a function of t (time): S(t), I(t) and R(t). For a specific disease in a specific population, these functions may be worked out in order to predict possible outbreaks and bring them under control.
disease with a short infectious period, such as measles
in the UK prior to the introduction of a vaccine
in 1968. Such diseases tend to occur in cycles of outbreaks due to the variation in number of susceptibles (S(t)) over time. During an epidemic
, the number of susceptible individuals falls rapidly as more of them are infected and thus enter the infectious and recovered compartments. The disease cannot break out again until the number of susceptibles has built back up as a result of babies being born into the susceptible compartment.
 Each member of the population typically progresses from susceptible to infectious to recovered. This can be shown as a flow diagram in which the boxes represent the different compartments and the arrows the transition between compartments.
Each member of the population typically progresses from susceptible to infectious to recovered. This can be shown as a flow diagram in which the boxes represent the different compartments and the arrows the transition between compartments.

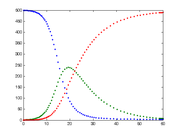
Between S and I, the transition rate is β I, where β is the contact rate, which -roughly speaking - takes into the account the probability of getting the disease in a contact between a susceptible and an infectious subject.
Between I and R, the transition rate is ν (simply the rate of recovery). If the duration of the infection is denoted D, then ν = 1/D, since an individual experiences one recovery in D units of time.
It is important to stress that here we assume that the permanence of each single subject in the epidemic states is a random variable with exponential distribution. More complex and realistic distributions (such as Erlang distributions) can be equally used with few modifications.

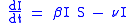
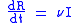
This model was for the first time proposed by O. Kermack and Anderson Gray McKendrick
, who had worked with the Nobel Laureate Ronald Ross
.
This system is non-linear, and does not admit a generic analytic solution. Nevertheless, significant results can be derived analytically.
Firstly note that from:
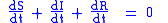
it follows that:
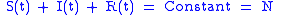
expressing in mathematical terms the constancy of population . Note that the above relationship implies that one can study the equation for only two of the three variables.
. Note that the above relationship implies that one can study the equation for only two of the three variables.
Secondly, we note that the dynamics of the infectious class depends on the following ratio:
the so-called basic reproduction number
(also called basic reproduction ratio
). This ratio is derived as the expected number of new infections from a single infection in a population where all subjects are susceptible
.
By dividing the first differential equation by the third, separating the variables
and integrating we get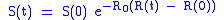
(where S(0) and R(0) are the initial numbers of, respectively, susceptible and removed subjects). Thus, in the limit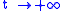 , the proportion of recovered individuals obeys the transcendental equation
, the proportion of recovered individuals obeys the transcendental equation
Consideration of this equation shows that generically, at the end of an epidemic, not all individuals have recovered, so some must remain susceptible. This means that the end of an epidemic is caused by the decline in the number of infected individuals rather than an absolute lack of susceptible subjects.
The role of the basic reproduction number
is extremely important. In fact, upon rewriting the equation for infectious individuals as follows: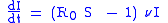
it yields that if: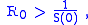
then: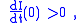
i.e. there will be a proper epidemic outbreak with an increase of the number of the infectious (which can reach a considerable fraction of the population). On the contrary, if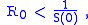
then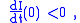
i.e. independently from the initial size of the susceptible population the disease can never cause a proper epidemic outbreak. As a consequence, it is clear that the basic reproduction number
is extremely important.

models the transition rate from the compartment of susceptible individuals to the compartment of infectious individuals, so that it is called the force of infection. However, for large classes of communicable diseases it is more realistic to consider a force of infection that does not depend on the absolute number of infectious subjects, but on their fraction (with respect to the total constant population ):
):
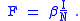
Capasso and, afterwards, other authors have proposed nonlinear forces of infection to model more realistically the contagion process.
 and birth rate equal to the death rate, and where a communicable disease is spreading. The model is:
and birth rate equal to the death rate, and where a communicable disease is spreading. The model is:
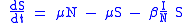
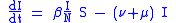
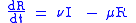
for which it holds:
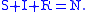
Also in this case we may define a basic reproduction number
:
which has threshold properties. In fact, independently from biologically meaningful initial values:
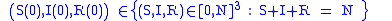
one can show that:
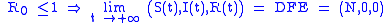
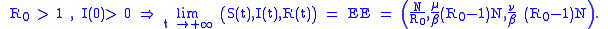
The point DFE is called the disease free equilibrium, whereas the point EE is called the Endemic Equilibrium. Since, with heuristic arguments, one may show that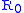 may be read as the average number of infections caused by a single infectious subject in a wholly susceptible population, the above relationship biologically means that if this number is less or equal than one the disease get extinct, whereas if this number is greater than one the disease will remain permanently endemic in the population.
may be read as the average number of infections caused by a single infectious subject in a wholly susceptible population, the above relationship biologically means that if this number is less or equal than one the disease get extinct, whereas if this number is greater than one the disease will remain permanently endemic in the population.
As a consequence, for many classes of diseases one should consider a force of infection with periodically ('seasonal') varying contact rate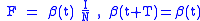
with period T equal to one year.
Thus, our model becomes
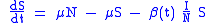

(the dynamics of recovered easily follows from ), idest a nonlinear set of differential equations with periodically varying parameters. It is well known that this class of dynamical systems may undergo very interesting and complex phenomena of nonlinear parametric resonance. It is easy to see that if:
), idest a nonlinear set of differential equations with periodically varying parameters. It is well known that this class of dynamical systems may undergo very interesting and complex phenomena of nonlinear parametric resonance. It is easy to see that if:
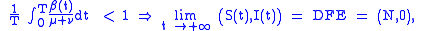
whereas if the integral is greater than one the disease will not die out and there may be such resonances. For example, considering the periodically varying contact rate as the 'input' of the system one has that the output is a periodic function whose period is a multiple of the period of the input.
This allowed to give a contribution to explain the poly-annual (typically biennial) epidemic outbreaks of some infectious diseases as interplay between the period of the contact rate oscillations and the pseudo-period of the damped oscillations near the endemic equilibrium.
Remarkably, in some cases the behavior may also be quasi-periodic or even chaotic.
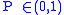 :
:
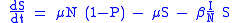
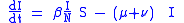
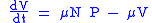
where V is the class of vaccinated subjects. It is immediate to show that:
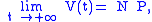
thus we shall deal with the long term behavior of S and I, for which it holds that:
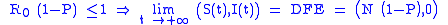

In other words if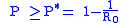
the vaccination program is successful in eradicating the disease, on the contrary it will remain endemic, although at lower levels than the case of absence of vaccinations. This means that the mathematical model suggests that for a disease whose basic reproduction number
may be as high as 18 one should have to vaccinate 94.4% of newborns in order to eradicate the disease.
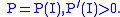
In such a case the eradication condition becomes:
i.e. the baseline vaccination rate should be greater than the "mandatory vaccination" threshold, which, in case of exemption, cannot hold. Thus, "rational" exemption might be myopic since it is based only on the current low incidence due to high vaccine coverage, instead taking into account future resurgence of infection due to coverage decline.
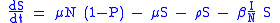

leading to the following eradication condition:
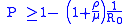
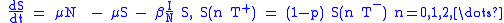

It is easy to see that by setting I=0 one obtains that the dynamics of the susceptible subjects is given by:
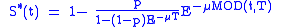
and that the eradication condition is:

 Assuming that the period of staying in the latent state is a random variable with exponential distribution with
Assuming that the period of staying in the latent state is a random variable with exponential distribution with
parameter a (i.e. the average latent period is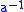 ), and also assuming the presence of vital dynamics with birth rate equal to death rate, we have the model:
), and also assuming the presence of vital dynamics with birth rate equal to death rate, we have the model:
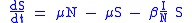
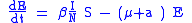
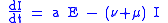
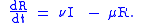
Of course, we have that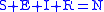 .
.
For this model, the basic reproduction number is:

Similarly to the SIR model, also in this case we have a Disease-Free-Equilibrium (N,0,0,0) and an Endemic Equilibrium EE, and one can show that, independently form biologically meaningful initial conditions
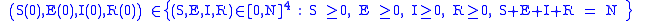
it holds that:
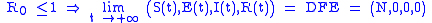
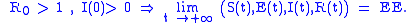
In case of periodically varying contact rate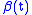 the condition for the global attractiveness of DFE is that the following linear system with periodic coefficients:
the condition for the global attractiveness of DFE is that the following linear system with periodic coefficients: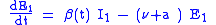
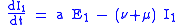
is stable (i.e. it has its Floquet's eigenvalues inside the unit circle in the complex plane).
, babies are not born into the susceptible compartment but are immune to the disease for the first few months of life due to protection from maternal antibodies (passed across the placenta
or through colostrum
). This added detail can be shown by including an M class (for maternally derived immunity) at the beginning of the model.

never completely recover and continue to carry
the infection, whilst not suffering the disease themselves. They may then move back into the infectious compartment and suffer symptoms (as in tuberculosis) or they may continue to infect others in their carrier state, while not suffering symptoms. The most famous example of this is probably Mary Mallon
, who infected 22 people with typhoid fever
. The carrier compartment is labelled C.
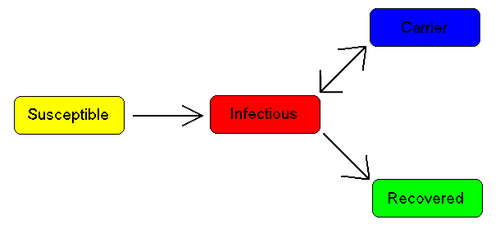
 Some infections, for example the group of those responsible for the common cold
Some infections, for example the group of those responsible for the common cold
, do not confer any long lasting immunity. Such infections do not have a recovered state and individuals become susceptible again after infection.
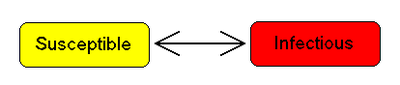 We have the model:
We have the model:
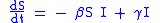
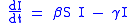
Note that denoting with N the total population it holds that:
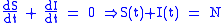
it follows that: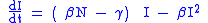
i.e. the dynamics of infectious is ruled by a logistic equation, so that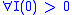 :
: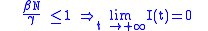
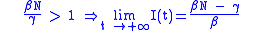
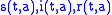 (to limit ourselves to the susceptible-infectious-removed scheme) such that:
(to limit ourselves to the susceptible-infectious-removed scheme) such that:
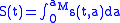
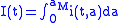
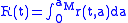
(where is the maximum admissible age)and their dynamics is not described, as one might think, by "simple" partial differential equations, but by integro-differential equation
is the maximum admissible age)and their dynamics is not described, as one might think, by "simple" partial differential equations, but by integro-differential equation
s:
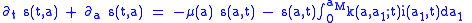
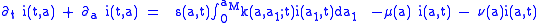

where:
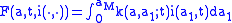
is the force of infection, which, of course, will depend, though the contact kernel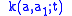 on the interactions between the ages.
on the interactions between the ages.
Complexity is added by the initial conditions for newborns (i.e. for a=0), that are straightforward for infectious and removed:
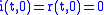
but that are nonlocal for the density of susceptible newborns:
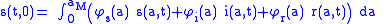
where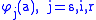 are the fertilities of the adults.
are the fertilities of the adults.
Moreover, defining now the density of the total population one obtains:
one obtains:
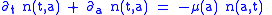
In the simplest case of equal fertilities in the three epidemic classes, we have that in oder to have demographic equilibrium the following necessary and sufficient condition linking the fertility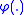 with the mortality
with the mortality 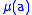 must hold:
must hold:
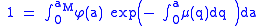
and the demographic equilibrium is

automatically ensuring the existence of the disease-free solution:
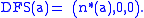
A basic reproduction number can be calculated as the spectral radius of an appropriate functional operator.
, in some cases deterministic models should cautiously be used. For example in case of seasonally varying contact rates the number of infectious subjects may reduce to infinitesimal values, thus maybe invalidating some results that are obtained in the field of chaotic epidemics.
Mathematical modelling in epidemiology
It is possible to mathematically model the progress of most infectious diseases to discover the likely outcome of an epidemic or to help manage them by vaccination...
in a large population
Population
A population is all the organisms that both belong to the same group or species and live in the same geographical area. The area that is used to define a sexual population is such that inter-breeding is possible between any pair within the area and more probable than cross-breeding with individuals...
, comprising many different individuals in various fields, the population diversity must be reduced to a few key characteristics which are relevant to the infection under consideration. For example, for most common childhood diseases that confer long-lasting immunity it makes sense to divide the population into those who are susceptible to the disease, those who are infected
Infectious disease
Infectious diseases, also known as communicable diseases, contagious diseases or transmissible diseases comprise clinically evident illness resulting from the infection, presence and growth of pathogenic biological agents in an individual host organism...
and those who have recovered and are immune
Immune system
An immune system is a system of biological structures and processes within an organism that protects against disease by identifying and killing pathogens and tumor cells. It detects a wide variety of agents, from viruses to parasitic worms, and needs to distinguish them from the organism's own...
. These subdivisions of the population are called compartments.
The SIR model
Standard convention labels these three compartments S (for susceptible), I (for infectious) and R (for recovered). Therefore, this model is called the SIR model.This is a good and simple
model for many infectious diseases including measles
Measles
Measles, also known as rubeola or morbilli, is an infection of the respiratory system caused by a virus, specifically a paramyxovirus of the genus Morbillivirus. Morbilliviruses, like other paramyxoviruses, are enveloped, single-stranded, negative-sense RNA viruses...
, mumps
Mumps
Mumps is a viral disease of the human species, caused by the mumps virus. Before the development of vaccination and the introduction of a vaccine, it was a common childhood disease worldwide...
and rubella
Rubella
Rubella, commonly known as German measles, is a disease caused by the rubella virus. The name "rubella" is derived from the Latin, meaning little red. Rubella is also known as German measles because the disease was first described by German physicians in the mid-eighteenth century. This disease is...
.
The letters also represent the number of people in each compartment at a particular time. To indicate that the numbers might vary over time (even if the total population size remains constant), we make the precise numbers a function of t (time): S(t), I(t) and R(t). For a specific disease in a specific population, these functions may be worked out in order to predict possible outbreaks and bring them under control.
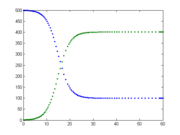
The SIR model is dynamic in three senses
As implied by the variable function of t, the model is dynamic in that the numbers in each compartment may fluctuate over time. The importance of this dynamic aspect is most obvious in an endemicEndemic (epidemiology)
In epidemiology, an infection is said to be endemic in a population when that infection is maintained in the population without the need for external inputs. For example, chickenpox is endemic in the UK, but malaria is not...
disease with a short infectious period, such as measles
Measles
Measles, also known as rubeola or morbilli, is an infection of the respiratory system caused by a virus, specifically a paramyxovirus of the genus Morbillivirus. Morbilliviruses, like other paramyxoviruses, are enveloped, single-stranded, negative-sense RNA viruses...
in the UK prior to the introduction of a vaccine
Vaccination
Vaccination is the administration of antigenic material to stimulate the immune system of an individual to develop adaptive immunity to a disease. Vaccines can prevent or ameliorate the effects of infection by many pathogens...
in 1968. Such diseases tend to occur in cycles of outbreaks due to the variation in number of susceptibles (S(t)) over time. During an epidemic
Epidemic
In epidemiology, an epidemic , occurs when new cases of a certain disease, in a given human population, and during a given period, substantially exceed what is expected based on recent experience...
, the number of susceptible individuals falls rapidly as more of them are infected and thus enter the infectious and recovered compartments. The disease cannot break out again until the number of susceptibles has built back up as a result of babies being born into the susceptible compartment.


Transition rates
For the full specification of the model, the arrows should be labeled with the transition rates between compartments.Between S and I, the transition rate is β I, where β is the contact rate, which -roughly speaking - takes into the account the probability of getting the disease in a contact between a susceptible and an infectious subject.
Between I and R, the transition rate is ν (simply the rate of recovery). If the duration of the infection is denoted D, then ν = 1/D, since an individual experiences one recovery in D units of time.
It is important to stress that here we assume that the permanence of each single subject in the epidemic states is a random variable with exponential distribution. More complex and realistic distributions (such as Erlang distributions) can be equally used with few modifications.
The SIR model without vital dynamics
A single epidemic outbreak is usually far more rapid than the vital dynamics of a population, thus, if the aim is to study the immediate consequences of a single epidemic, one may neglect the birth-death processes. In this case the SIR system described above can be expressed by the following set of ordinary differential equations:
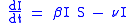
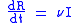
This model was for the first time proposed by O. Kermack and Anderson Gray McKendrick
Anderson Gray McKendrick
Anderson Gray McKendrick was a Scottish physician and epidemiologist pioneered the use of mathematical methods in epidemiology...
, who had worked with the Nobel Laureate Ronald Ross
Ronald Ross
Sir Ronald Ross KCB FRS was a British doctor who received the Nobel Prize for Physiology or Medicine in 1902 for his work on malaria. He was the first Indian-born person to win a Nobel Prize...
.
This system is non-linear, and does not admit a generic analytic solution. Nevertheless, significant results can be derived analytically.
Firstly note that from:
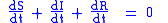
it follows that:
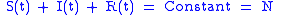
expressing in mathematical terms the constancy of population
 . Note that the above relationship implies that one can study the equation for only two of the three variables.
. Note that the above relationship implies that one can study the equation for only two of the three variables.Secondly, we note that the dynamics of the infectious class depends on the following ratio:

the so-called basic reproduction number
Basic reproduction number
In epidemiology, the basic reproduction number of an infection is the mean number of secondary cases caused by an individual infected soon after disease introduction into a population with no pre-existing immunity to the disease in the absence of interventions to control...
(also called basic reproduction ratio
Basic reproduction number
In epidemiology, the basic reproduction number of an infection is the mean number of secondary cases caused by an individual infected soon after disease introduction into a population with no pre-existing immunity to the disease in the absence of interventions to control...
). This ratio is derived as the expected number of new infections from a single infection in a population where all subjects are susceptible
.
By dividing the first differential equation by the third, separating the variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
and integrating we get
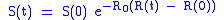
(where S(0) and R(0) are the initial numbers of, respectively, susceptible and removed subjects). Thus, in the limit
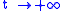 , the proportion of recovered individuals obeys the transcendental equation
, the proportion of recovered individuals obeys the transcendental equation
Consideration of this equation shows that generically, at the end of an epidemic, not all individuals have recovered, so some must remain susceptible. This means that the end of an epidemic is caused by the decline in the number of infected individuals rather than an absolute lack of susceptible subjects.
The role of the basic reproduction number
Basic reproduction number
In epidemiology, the basic reproduction number of an infection is the mean number of secondary cases caused by an individual infected soon after disease introduction into a population with no pre-existing immunity to the disease in the absence of interventions to control...
is extremely important. In fact, upon rewriting the equation for infectious individuals as follows:
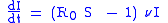
it yields that if:
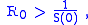
then:
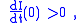
i.e. there will be a proper epidemic outbreak with an increase of the number of the infectious (which can reach a considerable fraction of the population). On the contrary, if
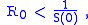
then
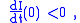
i.e. independently from the initial size of the susceptible population the disease can never cause a proper epidemic outbreak. As a consequence, it is clear that the basic reproduction number
Basic reproduction number
In epidemiology, the basic reproduction number of an infection is the mean number of secondary cases caused by an individual infected soon after disease introduction into a population with no pre-existing immunity to the disease in the absence of interventions to control...
is extremely important.
The force of infection
Note that in the above model the function:
models the transition rate from the compartment of susceptible individuals to the compartment of infectious individuals, so that it is called the force of infection. However, for large classes of communicable diseases it is more realistic to consider a force of infection that does not depend on the absolute number of infectious subjects, but on their fraction (with respect to the total constant population
 ):
):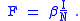
Capasso and, afterwards, other authors have proposed nonlinear forces of infection to model more realistically the contagion process.
The SIR model with vital dynamics and constant population
Considering a population characterized by a death rate and birth rate equal to the death rate, and where a communicable disease is spreading. The model is:
and birth rate equal to the death rate, and where a communicable disease is spreading. The model is: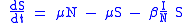
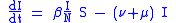
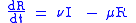
for which it holds:
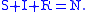
Also in this case we may define a basic reproduction number
Basic reproduction number
In epidemiology, the basic reproduction number of an infection is the mean number of secondary cases caused by an individual infected soon after disease introduction into a population with no pre-existing immunity to the disease in the absence of interventions to control...
:

which has threshold properties. In fact, independently from biologically meaningful initial values:
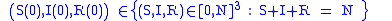
one can show that:
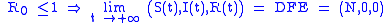
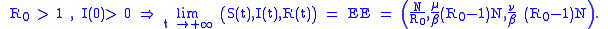
The point DFE is called the disease free equilibrium, whereas the point EE is called the Endemic Equilibrium. Since, with heuristic arguments, one may show that
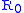 may be read as the average number of infections caused by a single infectious subject in a wholly susceptible population, the above relationship biologically means that if this number is less or equal than one the disease get extinct, whereas if this number is greater than one the disease will remain permanently endemic in the population.
may be read as the average number of infections caused by a single infectious subject in a wholly susceptible population, the above relationship biologically means that if this number is less or equal than one the disease get extinct, whereas if this number is greater than one the disease will remain permanently endemic in the population.Variable contact rates and pluriannual or chaotic epidemics
It is well known that the probability of getting a disease is not constant in the time. It is common experience that some diseases are more frequently present in the winter, and other in the summer in dependence of the weather. Moreover, for childhood diseases, there is a strong influence of the school calendar, so that during the school holidays the probability of getting such a disease dramatically decreases.As a consequence, for many classes of diseases one should consider a force of infection with periodically ('seasonal') varying contact rate
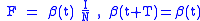
with period T equal to one year.
Thus, our model becomes
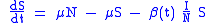

(the dynamics of recovered easily follows from
 ), idest a nonlinear set of differential equations with periodically varying parameters. It is well known that this class of dynamical systems may undergo very interesting and complex phenomena of nonlinear parametric resonance. It is easy to see that if:
), idest a nonlinear set of differential equations with periodically varying parameters. It is well known that this class of dynamical systems may undergo very interesting and complex phenomena of nonlinear parametric resonance. It is easy to see that if: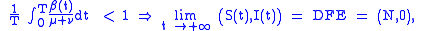
whereas if the integral is greater than one the disease will not die out and there may be such resonances. For example, considering the periodically varying contact rate as the 'input' of the system one has that the output is a periodic function whose period is a multiple of the period of the input.
This allowed to give a contribution to explain the poly-annual (typically biennial) epidemic outbreaks of some infectious diseases as interplay between the period of the contact rate oscillations and the pseudo-period of the damped oscillations near the endemic equilibrium.
Remarkably, in some cases the behavior may also be quasi-periodic or even chaotic.
Vaccinating the newborns
In presence of a communicable diseases, one of main tasks is that of eradicating it via prevention measures and, if possible, via the establishment of a mass vaccination program. Let us consider a disease for which the newborn are vaccinated (with a vaccine giving life-long immunity) at a rate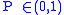 :
: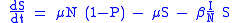
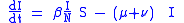
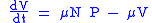
where V is the class of vaccinated subjects. It is immediate to show that:
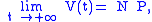
thus we shall deal with the long term behavior of S and I, for which it holds that:
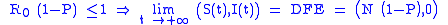

In other words if
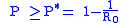
the vaccination program is successful in eradicating the disease, on the contrary it will remain endemic, although at lower levels than the case of absence of vaccinations. This means that the mathematical model suggests that for a disease whose basic reproduction number
Basic reproduction number
In epidemiology, the basic reproduction number of an infection is the mean number of secondary cases caused by an individual infected soon after disease introduction into a population with no pre-existing immunity to the disease in the absence of interventions to control...
may be as high as 18 one should have to vaccinate 94.4% of newborns in order to eradicate the disease.
Vaccination and information
Modern societies are facing the challenge of "rational" exemption, i.e. the family's decision to not vaccinate children as a consequence of a "rational" comparison between the perceived risk from infection and that from getting damages from the vaccine. In order to assess whether this behavior is really rational, i.e. if it can equally lead to the eradication of the disease, one may simply assume that the vaccination rate is an increasing function of the number of infectious subjects: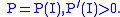
In such a case the eradication condition becomes:

i.e. the baseline vaccination rate should be greater than the "mandatory vaccination" threshold, which, in case of exemption, cannot hold. Thus, "rational" exemption might be myopic since it is based only on the current low incidence due to high vaccine coverage, instead taking into account future resurgence of infection due to coverage decline.
Vaccination of non newborns
In case there also are vaccinations of non newborn at a rate ρ the equation for the susceptible and vaccinated subject has to be modified as follows: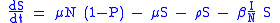

leading to the following eradication condition:
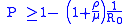
Pulse vaccination strategy
Pulse Vaccination Strategy is a vaccination policy consisting of periodical repetitions of 'impulsive' multi age-cohort vaccinations in a population, i.e. every T time units a constant fraction p of susceptible subjects is vaccinated in a relatively short (respect to the dynamics of the disease) time. This leads to the following impulsive differential equations for the susceptible and vaccinated subjects: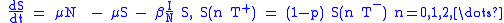

It is easy to see that by setting I=0 one obtains that the dynamics of the susceptible subjects is given by:
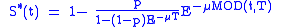
and that the eradication condition is:

The SEIR model
For many important infections there is a significant period of time during which the individual has been infected but is not yet infectious themselves. During this latent period the individual is in compartment E (for exposed).
parameter a (i.e. the average latent period is
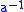 ), and also assuming the presence of vital dynamics with birth rate equal to death rate, we have the model:
), and also assuming the presence of vital dynamics with birth rate equal to death rate, we have the model: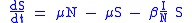
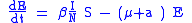
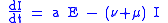
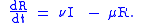
Of course, we have that
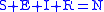 .
.For this model, the basic reproduction number is:

Similarly to the SIR model, also in this case we have a Disease-Free-Equilibrium (N,0,0,0) and an Endemic Equilibrium EE, and one can show that, independently form biologically meaningful initial conditions
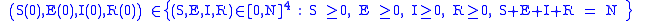
it holds that:
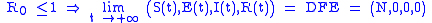
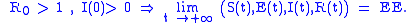
In case of periodically varying contact rate
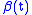 the condition for the global attractiveness of DFE is that the following linear system with periodic coefficients:
the condition for the global attractiveness of DFE is that the following linear system with periodic coefficients: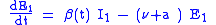
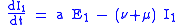
is stable (i.e. it has its Floquet's eigenvalues inside the unit circle in the complex plane).
The MSIR model
For many infections, including measlesMeasles
Measles, also known as rubeola or morbilli, is an infection of the respiratory system caused by a virus, specifically a paramyxovirus of the genus Morbillivirus. Morbilliviruses, like other paramyxoviruses, are enveloped, single-stranded, negative-sense RNA viruses...
, babies are not born into the susceptible compartment but are immune to the disease for the first few months of life due to protection from maternal antibodies (passed across the placenta
Placenta
The placenta is an organ that connects the developing fetus to the uterine wall to allow nutrient uptake, waste elimination, and gas exchange via the mother's blood supply. "True" placentas are a defining characteristic of eutherian or "placental" mammals, but are also found in some snakes and...
or through colostrum
Colostrum
Colostrum is a form of milk produced by the mammary glands of mammals in late pregnancy. Most species will generate colostrum just prior to giving birth...
). This added detail can be shown by including an M class (for maternally derived immunity) at the beginning of the model.

Carrier state
Some people who have had an infectious disease such as tuberculosisTuberculosis
Tuberculosis, MTB, or TB is a common, and in many cases lethal, infectious disease caused by various strains of mycobacteria, usually Mycobacterium tuberculosis. Tuberculosis usually attacks the lungs but can also affect other parts of the body...
never completely recover and continue to carry
Asymptomatic carrier
An asymptomatic carrier is a person or other organism that has contracted an infectious disease, but who displays no symptoms. Although unaffected by the disease themselves, carriers can transmit it to others...
the infection, whilst not suffering the disease themselves. They may then move back into the infectious compartment and suffer symptoms (as in tuberculosis) or they may continue to infect others in their carrier state, while not suffering symptoms. The most famous example of this is probably Mary Mallon
Mary Mallon
Mary Mallon , also known as Typhoid Mary, was the first person in the United States identified as an asymptomatic carrier of the pathogen associated with typhoid fever. She was presumed to have infected some 53 people, three of whom died, over the course of her career as a cook...
, who infected 22 people with typhoid fever
Typhoid fever
Typhoid fever, also known as Typhoid, is a common worldwide bacterial disease, transmitted by the ingestion of food or water contaminated with the feces of an infected person, which contain the bacterium Salmonella enterica, serovar Typhi...
. The carrier compartment is labelled C.

The SIS model

Common cold
The common cold is a viral infectious disease of the upper respiratory system, caused primarily by rhinoviruses and coronaviruses. Common symptoms include a cough, sore throat, runny nose, and fever...
, do not confer any long lasting immunity. Such infections do not have a recovered state and individuals become susceptible again after infection.

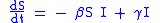
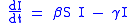
Note that denoting with N the total population it holds that:
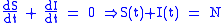
it follows that:
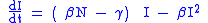
i.e. the dynamics of infectious is ruled by a logistic equation, so that
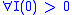 :
: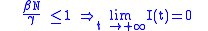
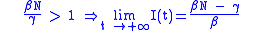
The influence of age: age-structured models
Maybe "the most specific parameter of biological system is the age" (M. Iannelli), and, especially for some infectious diseases, it has a deep influence on the dynamics of its spreading in a population. Many of the parameters we have seen may depend on age, and especially the contact rate, which summarizes the 'infectious effectiveness' of contacts between susceptible and infectious subjects. This effectiveness has, thus, to take into account both the age of the infectious and the age of the susceptible. Epidemic models modeling the age structure of a population are very complex. In fact, they are infinite dimensional model since we have to deal with density through the ages of the epidemic classes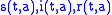 (to limit ourselves to the susceptible-infectious-removed scheme) such that:
(to limit ourselves to the susceptible-infectious-removed scheme) such that: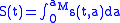
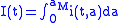
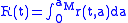
(where
 is the maximum admissible age)and their dynamics is not described, as one might think, by "simple" partial differential equations, but by integro-differential equation
is the maximum admissible age)and their dynamics is not described, as one might think, by "simple" partial differential equations, but by integro-differential equationIntegro-differential equation
An integro-differential equation is an equation which involves both integrals and derivatives of a function.The general first-order, linear integro-differential equation is of the form...
s:
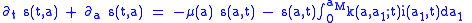
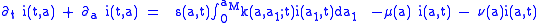

where:
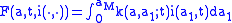
is the force of infection, which, of course, will depend, though the contact kernel
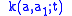 on the interactions between the ages.
on the interactions between the ages.Complexity is added by the initial conditions for newborns (i.e. for a=0), that are straightforward for infectious and removed:
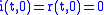
but that are nonlocal for the density of susceptible newborns:
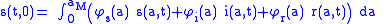
where
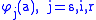 are the fertilities of the adults.
are the fertilities of the adults.Moreover, defining now the density of the total population
 one obtains:
one obtains: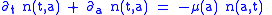
In the simplest case of equal fertilities in the three epidemic classes, we have that in oder to have demographic equilibrium the following necessary and sufficient condition linking the fertility
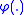 with the mortality
with the mortality 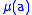 must hold:
must hold: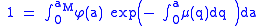
and the demographic equilibrium is

automatically ensuring the existence of the disease-free solution:
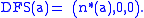
A basic reproduction number can be calculated as the spectral radius of an appropriate functional operator.
Deterministic versus stochastic epidemic models
It is important to stress that the deterministic models presented here are valid only in case of sufficiently large populations. Moreover, even in case of large populations, as pointed out among the firsts by M. S. BartlettM. S. Bartlett
Maurice Stevenson Bartlett FRS was an English statistician who made particular contributions to the analysis of data with spatial and temporal patterns...
, in some cases deterministic models should cautiously be used. For example in case of seasonally varying contact rates the number of infectious subjects may reduce to infinitesimal values, thus maybe invalidating some results that are obtained in the field of chaotic epidemics.
External links
- the Spatiotemporal Epidemiological ModelerSpatiotemporal Epidemiological ModelerThe Spatiotemporal Epidemiological Modeler is a free software available through the Eclipse Foundation. Originally developed by IBM Research, STEM is a framework and development tool designed to help scientists create and use spatial and temporal models of infectious disease. STEM uses a component...
(STEM) is an open source Epidemiological modeling system that uses the Eclipse Modeling FrameworkEclipse Modeling FrameworkEclipse Modeling Framework is an Eclipse-based modeling framework and code generation facility for building tools and other applications based on a structured data model...
from the Eclipse FoundationEclipse FoundationThe Eclipse Foundation is a not-for-profit, member supported corporation that hosts the open-source Eclipse Projects and helps cultivate both an open source community and an ecosystem of complementary products and services...
to allow rapid development of new models for infectious disease. External STEM site at Eclipse. - SIR model: Online experiments with JSXGraph
- SEIR Model simulator Free to use epidemics simulator using SEIR model. Systems Dynamics implementation of the SEIR model.

