
Complex reflection group
Encyclopedia
In mathematics
, a complex reflection group is a group
acting on a finite-dimensional complex vector space, that is generated by complex reflections: non-trivial elements that fix a complex hyperplane
in space pointwise. (Complex reflections are sometimes called pseudo reflections or unitary reflections or sometimes just reflections.)
R to C. In particular all Coxeter group
s or Weyl group
s give examples of complex reflection groups.
Any finite complex reflection group is a product of irreducible complex reflection groups, acting on the sum of the corresponding vector spaces. So it is sufficient to classify the irreducible complex reflection groups.
The finite irreducible complex reflection groups were classified by . They found an infinite family G(m,p,n) depending on 3 positive integer parameters (with p dividing m), and 34 exceptional cases, that they numbered from 4 to 37,
listed below. The group
G(m,p,n), of order mnn!/p, is the semidirect product of the abelian group
of order mn/p whose elements are (θa1,θa2, ...,θan), by the symmetric group Sn acting by permutations of the coordinates, where θ is a primitive mth root of unity and Σai≡ 0 mod p; it is an index p subgroup of the generalized symmetric group
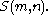
Special cases of G(m,p,n):
For more information, including diagrams, presentations, and codegrees of complex reflection groups, see the tables in .
). For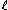 being the rank of the reflection group, the degrees
being the rank of the reflection group, the degrees 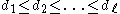 of the generators of the ring of invariants are called degrees of W and are listed in the column above headed "degrees". They also showed that many other invariants of the group are determined by the degrees as follows:
of the generators of the ring of invariants are called degrees of W and are listed in the column above headed "degrees". They also showed that many other invariants of the group are determined by the degrees as follows:
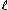 being the rank of the reflection group, the codegrees
being the rank of the reflection group, the codegrees 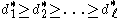 of W can be defined by
of W can be defined by
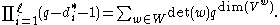
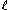 is generated by
is generated by 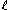 or by
or by  reflections. It is said to be well-generated if it is generated by
reflections. It is said to be well-generated if it is generated by 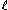 reflections ; it is proved that this is equivalent to the property
reflections ; it is proved that this is equivalent to the property 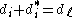 for all
for all 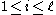 . For irreducible well-generated complex reflection groups, the Coxeter number
. For irreducible well-generated complex reflection groups, the Coxeter number 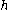 is defined to be the largest degree,
is defined to be the largest degree, 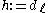 . A reducible complex reflection group is said to be well-generated if it is a product of irreducible well-generated complex reflection groups. Any finite real reflection group is well-generated.
. A reducible complex reflection group is said to be well-generated if it is a product of irreducible well-generated complex reflection groups. Any finite real reflection group is well-generated.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a complex reflection group is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
acting on a finite-dimensional complex vector space, that is generated by complex reflections: non-trivial elements that fix a complex hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
in space pointwise. (Complex reflections are sometimes called pseudo reflections or unitary reflections or sometimes just reflections.)
Classification
Any real reflection group becomes a complex reflection group if we extend the scalars fromR to C. In particular all Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s or Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
s give examples of complex reflection groups.
Any finite complex reflection group is a product of irreducible complex reflection groups, acting on the sum of the corresponding vector spaces. So it is sufficient to classify the irreducible complex reflection groups.
The finite irreducible complex reflection groups were classified by . They found an infinite family G(m,p,n) depending on 3 positive integer parameters (with p dividing m), and 34 exceptional cases, that they numbered from 4 to 37,
listed below. The group
G(m,p,n), of order mnn!/p, is the semidirect product of the abelian group
of order mn/p whose elements are (θa1,θa2, ...,θan), by the symmetric group Sn acting by permutations of the coordinates, where θ is a primitive mth root of unity and Σai≡ 0 mod p; it is an index p subgroup of the generalized symmetric group
Generalized symmetric group
In mathematics, the generalized symmetric group is the wreath product S := Z_m \wr S_n of the cyclic group of order m and the symmetric group on n letters.- Examples :...
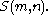
Special cases of G(m,p,n):
- G(1,1,n) is the Coxeter group An−1
- G(2,1,n) is the Coxeter group Bn = Cn
- G(2,2,n) is the Coxeter group Dn
- G(m,p,1) is a cyclic group of order m/p.
- G(m,m,2) is the Coxeter group I2(m) (and the Weyl group G2 when m = 6).
- The group G(m,p,n) acts irreducibly on Cn except in the cases m=1, n>1 (symmetric group) and G(2,2,2) (Klein 4 group), when Cn splits as a sum of irreducible representations of dimensions 1 and n−1.
- The only cases when two groups G(m,p,n) are isomorphic as complex reflection groups are that G(ma,pa,1) is isomorphic to G(mb,pb,1) for any positive integers a,b. However there are other cases when two such groups are isomorphic as abstract groups.
- The complex reflection group G(2,2,3) is isomorphic as a complex reflection group to G(1,1,4) restricted to a 3 dimensional space.
- The complex reflection group G(3,3,2) is isomorphic as a complex reflection group to G(1,1,3) restricted to a 2 dimensional space.
- The complex reflection group G(2p,p,1) is isomorphic as a complex reflection group to G(1,1,2) restricted to a 1 dimensional space.
List of irreducible complex reflection groups
There are a few duplicates in the first 3 lines of this list; see the previous section for details.- ST is the Shephard–Todd number of the reflection group.
- Rank is the dimension of the complex vector space the group acts on.
- Structure describes the structure of the group. The symbol * stands for a central productCentral productIn mathematics, especially in the field of group theory, the central product is way of producing a group from two smaller groups. The central product is similar to the direct product, but in the central product two isomorphic central subgroups of the smaller groups are merged into a single central...
of two groups. For rank 2, the quotient by the (cyclic) center is the group of rotations of a tetrahedron, octahedron, or icosahedron (T = Alt(4), O = Sym(4), I = Alt(5), of orders 12, 24, 60), as stated in the table. For the notation 21+4, see extra special groupExtra special groupIn group theory, a branch of mathematics, extra special groups are analogues of the Heisenberg group over finite fields whose size is a prime. For each prime p and positive integer n there are exactly two extra special groups of order p1+2n. Extra special groups often occur in centralizers of...
. - Order is the number of elements of the group.
- Reflections describes the number of reflections: 26412 means that there are 6 reflections of order 2 and 12 of order 4.
- Degrees gives the degrees of the fundamental invariants of the ring of polynomial invariants. For example, the invariants of group number 4 form a polynomial ring with 2 generators of degrees 4 and 6.
| ST | Rank | Structure and names | Order | Reflections | Degrees | Codegrees |
|---|---|---|---|---|---|---|
| 1 | n−1 | Symmetric group Symmetric group In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself... G(1,1,n) = Sym(n) | n! | 2n(n − 1)/2 | 2, 3, ...,n | 0,1,...,n − 2 |
| 2 | n | G(m,p,n) m > 1, n > 1, p|m (G(2,2,2) is reducible) | mnn!/p | 2mn(n−1)/2,dnφ(d) (d|m/p, d > 1) | m,2m,..,(n − 1)m; mn/p | 0,m,..., (n − 1)m if p < m; 0,m,...,(n − 2)m, (n − 1)m − n if p = m |
| 3 | 1 | Cyclic group G(m,1,1) = Zm | m | dφ(d) (d|m, d > 1) | m | 0 |
| 4 | 2 | Z2.T = 3[3]3 | 24 | 38 | 4,6 | 0,2 |
| 5 | 2 | Z6.T = 3[4]3 | 72 | 316 | 6,12 | 0,6 |
| 6 | 2 | Z4.T = 3[6]2 | 48 | 2638 | 4,12 | 0,8 |
| 7 | 2 | Z12.T = 〈3,3,3〉2 | 144 | 26316 | 12,12 | 0,12 |
| 8 | 2 | Z4.O = 4[3]4 | 96 | 26412 | 8,12 | 0,4 |
| 9 | 2 | Z8.O = 4[6]2 | 192 | 218412 | 8,24 | 0,16 |
| 10 | 2 | Z12.O = 4[4]3 | 288 | 26316412 | 12,24 | 0,12 |
| 11 | 2 | Z24.O = 〈4,3,2〉12 | 576 | 218316412 | 24,24 | 0,24 |
| 12 | 2 | Z2.O= GL2(F3) | 48 | 212 | 6,8 | 0,10 |
| 13 | 2 | Z4.O = 〈4,3,2〉2 | 96 | 218 | 8,12 | 0,16 |
| 14 | 2 | Z6.O = 3[8]2 | 144 | 212316 | 6,24 | 0,18 |
| 15 | 2 | Z12.O = 〈4,3,2〉6 | 288 | 218316 | 12,24 | 0,24 |
| 16 | 2 | Z10.I = 5[3]5 | 600 | 548 | 20,30 | 0,10 |
| 17 | 2 | Z20.I = 5[6]2 | 1200 | 230548 | 20,60 | 0,40 |
| 18 | 2 | Z30.I = 5[4]3 | 1800 | 340548 | 30,60 | 0,30 |
| 19 | 2 | Z60.I = 〈5,3,2〉30 | 3600 | 230340548 | 60,60 | 0,60 |
| 20 | 2 | Z6.I = 3[5]3 | 360 | 340 | 12,30 | 0,18 |
| 21 | 2 | Z12.I = 3[10]2 | 720 | 230340 | 12,60 | 0,48 |
| 22 | 2 | Z4.I = 〈5,3,2〉2 | 240 | 230 | 12,20 | 0,28 |
| 23 | 3 | W(H3) = Z2 × PSL2(5), Coxeter | 120 | 215 | 2,6,10 | 0,4,8 |
| 24 | 3 | W(J3(4)) = Z2 × PSL2(7), Klein (2,3,7) triangle group In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "... | 336 | 221 | 4,6,14 | 0,8,10 |
| 25 | 3 | W(L3) = W(P3) = 31+2.SL2(3), Hessian | 648 | 324 | 6,9,12 | 0,3,6 |
| 26 | 3 | W(M3) =Z2 ×31+2.SL2(3), Hessian | 1296 | 29 324 | 6,12,18 | 0,6,12 |
| 27 | 3 | W(J3(5)) = Z2 ×(Z3.Alt(6)), Valentiner Valentiner group In mathematics, the Valentiner group is the perfect triple cover of the alternating group on 6 points, and is a group of order 1080. It was found by in the form of an action of A6 on the complex projective plane, and was studied further by .... | 2160 | 245 | 6,12,30 | 0,18,24 |
| 28 | 4 | W(F4) = (SL2(3)* SL2(3)).(Z2 × Z2) Weyl | 1152 | 212+12 | 2,6,8,12 | 0,4,6,10 |
| 29 | 4 | W(N4) = (Z4*21 + 4).Sym(5) | 7680 | 240 | 4,8,12,20 | 0,8,12,16 |
| 30 | 4 | W(H4) = (SL2(5)*SL2(5)).Z2 Coxeter | 14400 | 260 | 2, 12, 20,30 | 0,10,18,28 |
| 31 | 4 | W(EN4) = W(O4) = (Z4*21 + 4).Sp4(2) | 46080 | 260 | 8,12,20,24 | 0,12,16,28 |
| 32 | 4 | W(L4) = Z3 × Sp4(3) | 155520 | 380 | 12,18,24,30 | 0,6,12,18 |
| 33 | 5 | W(K5) = Z2 ×Ω5(3) = Z2 × PSp4(3) = Z2 × PSU4(2) | 51840 | 245 | 4,6,10,12,18 | 0,6,8,12,14 |
| 34 | 6 | W(K6)= Z3.Ω(3).Z2, Mitchell's group Mitchell's group In mathematics, Mitchell's group is a complex reflection group in 6 complex dimensions of order 108 × 9!, introduced by . It has the structure 6.PSU4.2.... | 39191040 | 2126 | 6,12,18,24,30,42 | 0,12,18,24,30,36 |
| 35 | 6 | W(E6) = SO5(3) = O(2) = PSp4(3).Z2 = PSU4(2).Z2, Weyl | 51840 | 236 | 2,5,6,8,9,12 | 0,3,4,6,7,10 |
| 36 | 7 | W(E7) = Z2 ×Sp6(2), Weyl | 2903040 | 263 | 2,6,8,10,12,14,18 | 0,4,6,8,10,12,16 |
| 37 | 8 | W(E8)= Z2.O(2), Weyl | 696729600 | 2120 | 2,8,12,14,18,20,24,30 | 0,6,10,12,16,18,22,28 |
For more information, including diagrams, presentations, and codegrees of complex reflection groups, see the tables in .
Degrees
Shephard and Todd proved that a finite group acting on a complex vector space is a complex reflection group if and only if its ring of invariants is a polynomial ring (Chevalley–Shephard–Todd theoremChevalley–Shephard–Todd theorem
In mathematics, the Chevalley–Shephard–Todd theorem in invariant theory of finite groups states that the ring of invariants of a finite group acting on a complex vector space is a polynomial ring if and only if the group is generated by pseudoreflections. In the case of subgroups of the complex...
). For
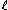 being the rank of the reflection group, the degrees
being the rank of the reflection group, the degrees 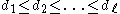 of the generators of the ring of invariants are called degrees of W and are listed in the column above headed "degrees". They also showed that many other invariants of the group are determined by the degrees as follows:
of the generators of the ring of invariants are called degrees of W and are listed in the column above headed "degrees". They also showed that many other invariants of the group are determined by the degrees as follows:- The center of an irreducible reflection group is cyclic of order equal to the greatest common divisor of the degrees.
- The order of a complex reflection group is the product of its degrees.
- The number of reflections is the sum of the degrees minus the rank.
- An irreducible complex reflection group comes from a real reflection group if and only if it has an invariant of degree 2.
- The degrees di satisfy the formula
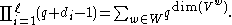
Codegrees
For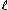 being the rank of the reflection group, the codegrees
being the rank of the reflection group, the codegrees 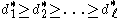 of W can be defined by
of W can be defined by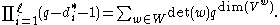
- For a real reflection group, the codegrees are the degrees minus 2.
- The number of reflection hyperplanes is the sum of the codegrees plus the rank.
Well-generated complex reflection groups
An irreducible complex reflection group of rank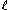 is generated by
is generated by 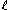 or by
or by  reflections. It is said to be well-generated if it is generated by
reflections. It is said to be well-generated if it is generated by 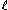 reflections ; it is proved that this is equivalent to the property
reflections ; it is proved that this is equivalent to the property 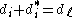 for all
for all 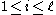 . For irreducible well-generated complex reflection groups, the Coxeter number
. For irreducible well-generated complex reflection groups, the Coxeter number 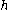 is defined to be the largest degree,
is defined to be the largest degree, 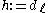 . A reducible complex reflection group is said to be well-generated if it is a product of irreducible well-generated complex reflection groups. Any finite real reflection group is well-generated.
. A reducible complex reflection group is said to be well-generated if it is a product of irreducible well-generated complex reflection groups. Any finite real reflection group is well-generated.
