Composite fermions
Encyclopedia
A composite fermion is the bound state of an electron and an even number of quantized vortices
, sometimes visually pictured as the bound state of an electron and, attached, an even number of magnetic flux quanta. Composite fermions were originally envisioned in the context of the fractional quantum Hall effect
, but subsequently took on a life of their own, exhibiting many other consequences and phenomena.
Vortices are an example of topological defect
, and also occur in other situations. Quantized vortices are found in type II superconductors, called Abrikosov vortices
. Classical vortices are relevant to the Berezenskii–Kosterlitz–Thouless transition in two-dimensional XY model
.
. Their behavior under such conditions is governed by the Coulomb repulsion alone, and they produce a strongly correlated quantum liquid. Experiments have shown that electrons minimize their interaction by capturing quantized vortices to become composite fermions. The interaction between composite fermions themselves is often negligible to a good approximation, which makes them the physical quasiparticle
s of this quantum liquid.
The signature quality of composite fermions, which is responsible for the otherwise unexpected behavior of this system, is that they experience a much smaller magnetic field than electrons. The magnetic field seen by composite fermions is given by
where
is the external magnetic field, 
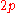is the number of vortices bound to composite fermion (also called the vorticity or the vortex charge of the composite fermion), 
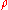is the particle density in two dimensions, and 
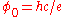is called the “flux quantum” (which differs from the superconducting flux quantum
by a factor of two). The effective magnetic field is a direct manifestation of the existence of composite fermions, and also embodies a fundamental distinction between electrons and composite fermions.
Sometimes it is said that electrons "swallow"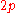
flux quanta each to transform into composite fermions, and the composite fermions then experience the residual magnetic field 
More accurately, the vortices bound to electrons produce their own geometric phase
s which partly cancel the Aharonov–Bohm phase due to the external magnetic field to generate a net geometric phase that can be modeled as an Aharonov–Bohm phase in an effective magnetic field
The behavior of composite fermions is similar to that of electrons in an effective magnetic field
Electrons form Landau levels in a magnetic field, and the number of filled Landau levels is called the filling factor, given by the expression 
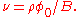Composite fermions form Landau-like levels in the effective magnetic field 
which are called composite fermion Landau levels or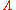 
levels. One defines the filling factor for composite fermions as 
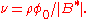This gives the following relation between the electron and composite fermion filling factors
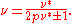
The minus sign occurs when the effective magnetic field is antiparallel to the applied magnetic field, which happens when the geometric phase from the vortices overcompensate the Aharonov–Bohm phase.
(or filling factor 
) turn into weakly interacting composite fermions at a magnetic field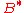 
(or composite fermion filling factor 
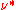). This allows an effectively single-particle explanation of the otherwise complex many-body behavior, with the interaction between electrons manifesting as an effective kinetic energy of composite fermions. Here are some of the phenomena arising from composite fermions:
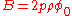, where the filling factor for composite fermions is 
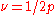. Here, composite fermions make a Fermi sea. This Fermi sea has been observed in a number of experiments, which also measure the Fermi wave vector.
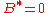, composite fermions execute semiclassical cyclotron orbits. These have been observed by coupling to surface acoustic waves, resonance peaks in antidot superlattice, and magnetic focusing. The radius of the cyclotron orbits is consistent with the effective magnetic field 
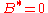and is sometimes an order of magnitude or more larger than the radius of the cyclotron orbit of an electron at the externally applied magnetic field 
. Also, the observed direction of trajectory is opposite to that of electrons when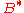 
is anti-parallel to 
.
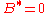, quantum oscillations are observed that are periodic in 
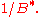These are Shubnikov–de Haas oscillations of composite fermions. These oscillations arise from the quantization of the semiclassical cyclotron orbits of composite fermions into composite fermion Landau levels. From the analysis of the Shubnikov–de Haas experiments, one can deduce the effective mass and the quantum lifetime of composite fermions.
or decrease in temperature and disorder, composite fermions exhibit integer quantum Hall effect. The integer fillings of composite fermions, 
, correspond to the electrons fillings
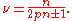
Combined with
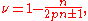
which are obtained by attaching vortices to holes in the lowest Landau level, these constitute the prominently observed sequences of fractions. Examples are
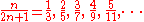
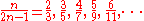
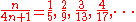
The fractional quantum Hall effect
of electrons is thus explained as the integer quantum Hall effect of composite fermions. It results in fractionally quantized Hall plateaus at
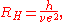
with
given by above quantized values. These sequences terminate at the composite fermion Fermi sea. Note that the fractions have odd denominators, which follows from the even vorticity of composite fermions.
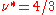produces the fraction 4/11, which does not belong to the primary sequences.
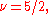has been observed. Here the second Landau level is half full, but the state cannot be a Fermi sea of composite fermions, because the Fermi sea is gapless and does not show quantum Hall effect. This state is viewed as a “superconductor “ of composite fermion, arising from a weak attractive interaction between composite fermions at this filling factor. The pairing of composite fermions opens a gap and produces a fractional quantum Hall effect.
Here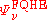
is the wave function of interacting electrons at filling factor 
; 
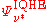is the wave function for weakly interacting electrons at 
; 
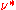is the number of electrons or composite fermions; 
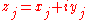is the coordinate of the 
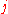th particle; and 
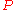is an operator that projects the wave function into the lowest Landau level. This provides an explicit mapping between the integer and the fractional quantum Hall effects. Multiplication by 
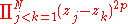attaches 
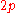vortices to each electron to convert it into a composite fermion. The right hand side is thus interpreted as describing composite fermions at filling factor 
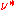. The above mapping gives wave functions for both the ground and excited states of the fractional quantum Hall states in terms of the corresponding known wave functions for the integral quantum Hall states. The latter do not contain any adjustable parameters for 
, so the FQHE wave functions do not contain any adjustable parameters at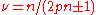 
.
Comparisons with exact results show that these wave functions are quantitatively accurate. They can be used to compute a number of measurable quantities, such as the excitation gaps and exciton dispersions, the phase diagram of composite fermions with spin, the composite fermion mass, etc. For
they reduce to the Laughlin wavefunction
at fillings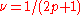
.
Quantum vortex
In physics, a quantum vortex is a topological defect exhibited in superfluids and superconductors. Superfluids and superconductors are states of matter without friction. They exist only at very low temperatures. The existence of these quantum vortices was independently predicted by Richard Feynman...
, sometimes visually pictured as the bound state of an electron and, attached, an even number of magnetic flux quanta. Composite fermions were originally envisioned in the context of the fractional quantum Hall effect
Fractional quantum Hall effect
The fractional quantum Hall effect is a physical phenomenon in which the Hall conductance of 2D electrons shows precisely quantised plateaus at fractional values of e^2/h. It is a property of a collective state in which electrons bind magnetic flux lines to make new quasiparticles, and excitations...
, but subsequently took on a life of their own, exhibiting many other consequences and phenomena.
Vortices are an example of topological defect
Topological defect
In mathematics and physics, a topological soliton or a topological defect is a solution of a system of partial differential equations or of a quantum field theory homotopically distinct from the vacuum solution; it can be proven to exist because the boundary conditions entail the existence of...
, and also occur in other situations. Quantized vortices are found in type II superconductors, called Abrikosov vortices
Abrikosov vortex
In superconductivity, an Abrikosov vortex is a vortex of supercurrent in a type-II superconductor. The supercurrent circulates around the normal core of the vortex. The core has a size \sim\xi — the superconducting coherence length...
. Classical vortices are relevant to the Berezenskii–Kosterlitz–Thouless transition in two-dimensional XY model
XY model
The classical XY model is a model of statistical mechanics. It is the special case of the n-vector model for n=2.-Definition:...
.
Description
When electrons are confined to two dimensions, cooled to very low temperatures, and subjected to a strong magnetic field, their kinetic energy is quenched due to Landau level quantizationLandau quantization
Landau quantization in quantum mechanics is the quantization of the cyclotron orbits of charged particles in magnetic fields. As a result, the charged particles can only occupy orbits with discrete energy values, called Landau levels. The Landau levels are degenerate, with the number of electrons...
. Their behavior under such conditions is governed by the Coulomb repulsion alone, and they produce a strongly correlated quantum liquid. Experiments have shown that electrons minimize their interaction by capturing quantized vortices to become composite fermions. The interaction between composite fermions themselves is often negligible to a good approximation, which makes them the physical quasiparticle
Quasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
s of this quantum liquid.
The signature quality of composite fermions, which is responsible for the otherwise unexpected behavior of this system, is that they experience a much smaller magnetic field than electrons. The magnetic field seen by composite fermions is given by
where
is the external magnetic field, 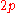is the number of vortices bound to composite fermion (also called the vorticity or the vortex charge of the composite fermion), 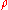is the particle density in two dimensions, and 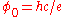is called the “flux quantum” (which differs from the superconducting flux quantumMagnetic flux quantum
The magnetic flux quantum Φ0 is the quantum of magnetic flux passing through a superconductor. The phenomenon of flux quantization was discovered B. S. Deaver and W. M. Fairbank and, independently, by R. Doll and M. Nabauer, in 1961...
by a factor of two). The effective magnetic field is a direct manifestation of the existence of composite fermions, and also embodies a fundamental distinction between electrons and composite fermions.
Sometimes it is said that electrons "swallow"
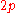flux quanta each to transform into composite fermions, and the composite fermions then experience the residual magnetic field More accurately, the vortices bound to electrons produce their own geometric phaseGeometric phase
In classical and quantum mechanics, the geometric phase, Pancharatnam–Berry phase , Pancharatnam phase or most commonly Berry phase, is a phase acquired over...
s which partly cancel the Aharonov–Bohm phase due to the external magnetic field to generate a net geometric phase that can be modeled as an Aharonov–Bohm phase in an effective magnetic field
The behavior of composite fermions is similar to that of electrons in an effective magnetic field
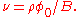Electrons form Landau levels in a magnetic field, and the number of filled Landau levels is called the filling factor, given by the expression Composite fermions form Landau-like levels in the effective magnetic field which are called composite fermion Landau levels or 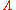levels. One defines the filling factor for composite fermions as 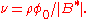This gives the following relation between the electron and composite fermion filling factors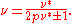The minus sign occurs when the effective magnetic field is antiparallel to the applied magnetic field, which happens when the geometric phase from the vortices overcompensate the Aharonov–Bohm phase.
Experimental manifestations
The main statement of composite fermion theory is that the strongly correlated electrons at a magnetic field (or filling factor ) turn into weakly interacting composite fermions at a magnetic field 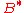(or composite fermion filling factor 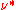). This allows an effectively single-particle explanation of the otherwise complex many-body behavior, with the interaction between electrons manifesting as an effective kinetic energy of composite fermions. Here are some of the phenomena arising from composite fermions:Fermi sea
The effective magnetic field for composite fermions vanishes for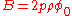, where the filling factor for composite fermions is 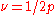. Here, composite fermions make a Fermi sea. This Fermi sea has been observed in a number of experiments, which also measure the Fermi wave vector.Cyclotron orbits
As the magnetic field is moved slightly away from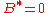, composite fermions execute semiclassical cyclotron orbits. These have been observed by coupling to surface acoustic waves, resonance peaks in antidot superlattice, and magnetic focusing. The radius of the cyclotron orbits is consistent with the effective magnetic field 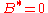and is sometimes an order of magnitude or more larger than the radius of the cyclotron orbit of an electron at the externally applied magnetic field . Also, the observed direction of trajectory is opposite to that of electrons when 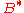is anti-parallel to .Cyclotron resonance
In addition to the cyclotron orbits, cyclotron resonance of composite fermions has also been observed by photoluminescence.Shubnikov de Haas oscillations
As the magnetic field is moved further away from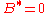, quantum oscillations are observed that are periodic in 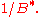These are Shubnikov–de Haas oscillations of composite fermions. These oscillations arise from the quantization of the semiclassical cyclotron orbits of composite fermions into composite fermion Landau levels. From the analysis of the Shubnikov–de Haas experiments, one can deduce the effective mass and the quantum lifetime of composite fermions.Integer quantum Hall effect
With further increase in or decrease in temperature and disorder, composite fermions exhibit integer quantum Hall effect. The integer fillings of composite fermions, , correspond to the electrons fillings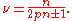Combined with
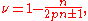
which are obtained by attaching vortices to holes in the lowest Landau level, these constitute the prominently observed sequences of fractions. Examples are
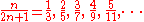
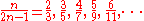
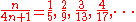
The fractional quantum Hall effect
Fractional quantum Hall effect
The fractional quantum Hall effect is a physical phenomenon in which the Hall conductance of 2D electrons shows precisely quantised plateaus at fractional values of e^2/h. It is a property of a collective state in which electrons bind magnetic flux lines to make new quasiparticles, and excitations...
of electrons is thus explained as the integer quantum Hall effect of composite fermions. It results in fractionally quantized Hall plateaus at
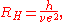
with
given by above quantized values. These sequences terminate at the composite fermion Fermi sea. Note that the fractions have odd denominators, which follows from the even vorticity of composite fermions.Fractional quantum Hall effect
The above sequences exhaust most, but not all, observed fractions. Other fractions have been observed, which arise from a weak residual interaction between composite fermions, and are thus more delicate. A number of these are understood as fractional quantum Hall effect of composite fermions. For example, the fractional quantum Hall effect of composite fermions at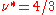 produces the fraction 4/11, which does not belong to the primary sequences.Superconductivity
An even denominators fraction,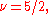 has been observed. Here the second Landau level is half full, but the state cannot be a Fermi sea of composite fermions, because the Fermi sea is gapless and does not show quantum Hall effect. This state is viewed as a “superconductor “ of composite fermion, arising from a weak attractive interaction between composite fermions at this filling factor. The pairing of composite fermions opens a gap and produces a fractional quantum Hall effect.Excitons
The neutral excitations of various fractional quantum Hall states are excitons of composite fermions, that is, particle hole pairs of composite fermions. The energy dispersion of these excitons has been measured by light scattering and phonon scattering.Spin
At high magnetic fields the spin of composite fermions is frozen, but it is observable at relatively low magnetic fields. The fan diagram of the composite fermion Landau levels has been determined by transport, and shows both spin-up and spin-down composite fermion Landau levels. The fractional quantum Hall states as well as composite fermion Fermi sea are also partially spin polarized for relatively low magnetic fields.Effective magnetic field
The effective magnetic field of composite fermions has been confirmed by the similarity of the fractional and the integer quantum Hall effects, observation of Fermi sea at half filled Landau level, and measurements of the cyclotron radius.Mass
The mass of composite fermions has been determined from the measurements of: the effective cyclotron energy of composite fermions; the temperature dependence of Shubnikov–de Haas oscillations; energy of the cyclotron resonance; spin polarization of the Fermi sea; and quantum phase transitions between states with different spin polarizations. Its typical value in GaAs systems is on the order of the electron mass in vacuum. (It is unrelated to the electron band mass in GaAs, which is 0.07 of the electron mass in vacuum.)Theoretical formulations
Much of the experimental phenomenology can be understood from the qualitative picture of composite fermions in an effective magnetic field. In addition, composite fermions also lead to a detailed and accurate microscopic theory of this quantum liquid. Two approaches have proved useful.Trial wave functions
The following trial wave functions embody the composite fermion physics:Here
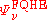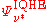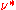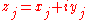is the wave function of interacting electrons at filling factor ; is the wave function for weakly interacting electrons at ; is the number of electrons or composite fermions; is the coordinate of the 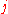th particle; and 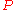is an operator that projects the wave function into the lowest Landau level. This provides an explicit mapping between the integer and the fractional quantum Hall effects. Multiplication by 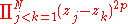attaches 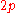vortices to each electron to convert it into a composite fermion. The right hand side is thus interpreted as describing composite fermions at filling factor 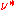. The above mapping gives wave functions for both the ground and excited states of the fractional quantum Hall states in terms of the corresponding known wave functions for the integral quantum Hall states. The latter do not contain any adjustable parameters for , so the FQHE wave functions do not contain any adjustable parameters at 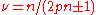.Comparisons with exact results show that these wave functions are quantitatively accurate. They can be used to compute a number of measurable quantities, such as the excitation gaps and exciton dispersions, the phase diagram of composite fermions with spin, the composite fermion mass, etc. For
they reduce to the Laughlin wavefunctionLaughlin wavefunction
In condensed matter physics, the Laughlin wavefunction is an ansatz, proposed by Robert Laughlin for the ground state of a two-dimensional electron gas placed in a uniform background magnetic field in the presence of a uniform jellium background when the filling factor of the lowest Landau level is...
at fillings
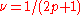.Chern–Simons field theory
Another formulation of the composite fermion physics is through a Chern–Simons field theory, wherein flux quanta are attached to electrons by a singular gauge transformation. At the mean field approximation the physics of free fermions in an effective field is recovered. Perturbation theory at the level of the random phase approximation captures many of the properties of composite fermions.See also
- Fractional quantum Hall effectFractional quantum Hall effectThe fractional quantum Hall effect is a physical phenomenon in which the Hall conductance of 2D electrons shows precisely quantised plateaus at fractional values of e^2/h. It is a property of a collective state in which electrons bind magnetic flux lines to make new quasiparticles, and excitations...
External links
- Nobel Lecture: The fractional quantum Hall effect by H.L. StormerHorst Ludwig StörmerHorst Ludwig Störmer is a German physicist who shared the 1998 Nobel Prize in Physics with Daniel Tsui and Robert Laughlin. The three shared the prize "for their discovery of a new form of quantum fluid with fractionally charged excitations"...
- Composite Fermions: New particles in the fractional quantum Hall effect, by H. Störmer and D. Tsui, Physics News in 1994, American Institute of Physics 1995, p. 33.
- Composite Fermion at the Pennsylvania State UniversityPennsylvania State UniversityThe Pennsylvania State University, commonly referred to as Penn State or PSU, is a public research university with campuses and facilities throughout the state of Pennsylvania, United States. Founded in 1855, the university has a threefold mission of teaching, research, and public service...
- Composite Fermions - von Klitzing's department at the Max Planck Institute
- Composite fermions are real at the [Physics News Update, American Institute of PhysicsAmerican Institute of PhysicsThe American Institute of Physics promotes science, the profession of physics, publishes physics journals, and produces publications for scientific and engineering societies. The AIP is made up of various member societies...
- Half filled Landau level yields intriguing data and theory in Physics TodayPhysics TodayPhysics Today, created in 1948, is the membership journal of the American Institute of Physics. It is provided to 130,000 members of twelve physics societies, including the American Physical Society...
- The composite fermion: A quantum particle and its quantum fluids in Physics TodayPhysics TodayPhysics Today, created in 1948, is the membership journal of the American Institute of Physics. It is provided to 130,000 members of twelve physics societies, including the American Physical Society...