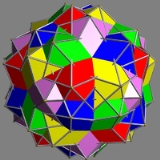
Compound of five icosahedra
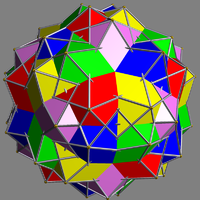Type	Uniform compound Uniform polyhedron compound A uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.The uniform polyhedron compounds were first enumerated by John Skilling...
Index	UC47
Polyhedra	5 icosahedra Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
Faces	40+60 Triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s
Edges	150
Vertices	60
Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...	icosahedral Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...  (Ih)
Subgroup Subgroup In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...  restricting to one constituent	pyritohedral Tetrahedral symmetry 150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...  (Th)

This uniform polyhedron compound

Uniform polyhedron compound

A uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.The uniform polyhedron compounds were first enumerated by John Skilling...

 is a composition of 5 icosahedra

Icosahedron

In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....

. It has icosahedral

Icosahedral symmetry

A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...

 symmetry I_h.

The triangles in this compound decompose into two orbits under action of the symmetry group: 40 of the triangles lie in coplanar pairs in icosahedral planes, while the other 60 lie in unique planes.

Cartesian coordinates

Cartesian coordinates for the vertices of this compound are all the cyclic permutations of

(0, ±2, ±2τ)

(±τ⁻¹, ±1, ±(1+τ²))

(±τ, ±τ², ±(2τ−1))

where τ = (1+√5)/2 is the golden ratio

Golden ratio

In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...

(sometimes written φ).