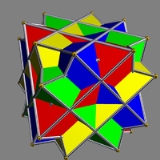
Compound of four octahedra
Type	Uniform compound Uniform polyhedron compound A uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.The uniform polyhedron compounds were first enumerated by John Skilling...
Index	UC12
Convex hull Convex hull In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....	Nonuniform truncated cube Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....
Polyhedra	4 octahedra Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
Faces	8+24 triangles
Edges	48
Vertices	24
Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...	octahedral Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...  (Oh)
Subgroup Subgroup In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...  restricting to one constituent	3-fold antiprismatic Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...  (D3d)

This uniform polyhedron compound

Uniform polyhedron compound

A uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.The uniform polyhedron compounds were first enumerated by John Skilling...

 is a symmetric arrangement of 4 octahedra

Octahedron

In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....

, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by 60 degrees about a separate axis (that passes through the centres of two opposite octahedral faces).

Cartesian coordinates

Cartesian coordinates for the vertices of this compound are all the permutations of

(±2, ±1, ±2)

See also

• Compound of three octahedra
  Compound of three octahedra
  In mathematics, the compound of three octahedra or octahedron 3-compound is a polyhedral compound formed from three regular octahedra, all sharing a common center but rotated with respect to each other. Although appearing earlier in the mathematical literature, it was rediscovered and popularized...
  
  
• Compound of five octahedra
  Compound of five octahedra
  This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.- As a stellation :It is the second stellation of the icosahedron, and given as Wenninger model index 23....
  
  
• Compound of ten octahedra
  Compound of ten octahedra
  These uniform polyhedron compounds are symmetric arrangements of 10 octahedra, considered as triangular antiprisms, aligned with the axes of three-fold rotational symmetry of an icosahedron...
  
  
• Compound of twenty octahedra
  Compound of twenty octahedra
  This uniform polyhedron compound is a symmetric arrangement of 20 octahedra . It is a special case of the compound of 20 octahedra with rotational freedom, in which pairs of octahedral vertices coincide.- Related polyhedra :...