Compound of six cubes with rotational freedom
Type	Uniform compound Uniform polyhedron compound A uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.The uniform polyhedron compounds were first enumerated by John Skilling...
Index	UC7
Polyhedra	6 cubes
Faces	12+24 squares Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
Edges	72
Vertices	48
Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...	octahedral Octahedral symmetry 150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...  (Oh)
Subgroup Subgroup In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...  restricting to one constituent	4-fold rotational Cyclic symmetries This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...  (C4h)

This uniform polyhedron compound

Uniform polyhedron compound

A uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.The uniform polyhedron compounds were first enumerated by John Skilling...

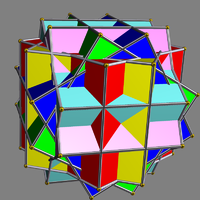
 is a symmetric arrangement of 6 cubes, considered as square prisms. It can be constructed by superimposing six identical cubes, and then rotating them in pairs about the three axes that pass through the centres of two opposite cubic faces. Each cube is rotated by an equal (and opposite, within a pair) angle θ.

When θ=0, all six cubes coincide. When θ is 45 degrees, the cubes coincide in pairs yielding (two superimposed copies of) the compound of three cubes

Compound of three cubes

This uniform polyhedron compound is a symmetric arrangement of 3 cubes, considered as square prisms. It can be constructed by superimposing three identical cubes, and then rotating each by 45 degrees about a separate axis .This compound famously appears in the lithograph print Waterfall by M.C....

.

Cartesian coordinates

Cartesian coordinates for the vertices of this compound are all the permutations of

(±(cosθ+sinθ), ±(cosθ−sinθ), ±1)