Compressed sensing
Encyclopedia
Compressed sensing, also known as compressive sensing, compressive sampling and sparse sampling, is a technique for finding sparse solutions to underdetermined linear systems
. In electrical engineering
, particularly in signal processing
, compressed sensing is the process of acquiring and reconstructing a signal that is supposed to be sparse
or compressible
.
techniques. In statistics, the least-squares method was complemented by the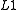
-norm , which was introduced by Laplace. Following the introduction of linear programming
and Dantzig's simplex algorithm
, the L1-norm was used in computational statistics
. In statistical theory, the L1-norm was used by George W. Brown
and later writers on median-unbiased estimators. It was used by Peter Huber and others working on robust statistics
. The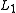
norm was also used in signal processing, for example, in the 1970s, when seismologists constructed images of reflective layers within the earth based on data that did not seem to satisfy the Nyquist–Shannon criterion
. It was used in matching pursuit
in 1993, the LASSO estimator by Robert Tibshirani
in 1996 and Basis Pursuit in 1998. There were theoretical results describing when these algorithms recovered sparse solutions, but the required type and number of measurements were sub-optimal and subsequently greatly improved by compressed sensing. Around 2004 Emmanuel Candès
, Terence Tao
and David Donoho
discovered important results on the minimum number of data needed to reconstruct an image even though the number of data would be deemed insufficient by the Nyquist–Shannon criterion.
of linear equations has more unknowns than equations and generally has an infinite number of solutions. However, if there is a unique sparse solution to the underdetermined system, then the Compressed Sensing framework allows the recovery of that solution. Not all underdetermined systems of linear equations have a sparse solution.
, that is, they contain many coefficients close to or equal to zero, when represented in some domain. This is the same insight used in many forms of lossy compression.
Compressed sensing typically starts with taking a weighted linear combination of samples also called compressive measurements in a basis
different from the basis in which the signal is known to be sparse. The results found by David Donoho
, Emmanuel Candès
, Justin Romberg and Terence Tao
showed that the number of these compressive measurements can be small and still contain nearly all the useful information. Therefore, the task of converting the image back into the intended domain involves solving an underdetermined
matrix equation since the number of compressive measurements taken is smaller than the number of pixels in the full image. However, adding the constraint that the initial signal is sparse enables one to solve this underdetermined
system of linear equations.
The least-squares solution to such problems is to minimize the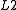
norm—that is, minimize the amount of energy in the system. This is usually simple mathematically (involving only a matrix multiplication
by the pseudo-inverse of the basis sampled in). However, this leads to poor results for many practical applications, for which the unknown coefficients have nonzero energy.
To enforce the sparsity constraint when solving for the underdetermined system of linear equations
, one can minimize the number of nonzero components of the solution.
The function counting the number of non-zero components of a vector was called the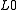
"norm" by David Donoho. The quotation marks served two warnings. First, the number-of-nonzeros 
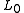-"norm" is not a proper F-norm
, because it is not continuous in its scalar argument: nnzs(αx) is constant as α approaches zero. Unfortunately, later authors have neglected Donoho's quotation marks and abused terminology—clashing with the established use of the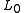
norm for the space of measurable functions (equipped with an appropriate metric) or for the space
of sequences with F–norm
.
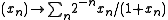Candès
. et. al., proved that for many problems it is probable that the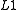
norm is equivalent to the 
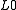norm, in a technical sense: This equivalence result allows one to solve the L1 problem, which is easier than the 
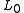problem. Finding the candidate with the smallest 
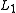norm can be expressed relatively easily as a linear program, for which efficient solution methods already exist. When measurements may contain a finite amount of noise, basis pursuit denoising is preferred over linear programming, since it preserves sparsity in the face of noise and can be solved faster than an exact linear program.
s, group testing
, heavy hitters, sparse coding
, multiplexing
, sparse sampling, and finite rate of innovation. Imaging techniques having a strong affinity with compressive sensing include coded aperture
and computational photography
.
Starting with the single-pixel camera from Rice University
, an up-to-date list of the most recent implementations of compressive sensing in hardware at different technology readiness level
is available. Some hardware implementation (like the one used in MRI or compressed genotyping) do not require an actual physical change, whereas other hardware require substantial re-engineering to perform this new type of sampling. Similarly, a number of hardware implementations already existed before 2004; however, while they were acquiring signals in a compressed manner, they generally did not use compressive sensing reconstruction techniques to reconstruct the original signal. The result of these reconstruction were suboptimal and have been greatly enhanced thanks to compressive sensing.
. Some aspects of compressed sensing were featured in Wired's "Engineers Test Highly Accurate Face Recognition". A more recent article in Wired described compressed sensing as a full-fledged technique in "Using Math to Turn Lo-Res Datasets Into Hi-Res Samples". Because the article was talking about sampling for MRI, some confusion might have occurred.
Underdetermined system
In mathematics, a system of linear equations is considered underdetermined if there are fewer equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
. In electrical engineering
Electrical engineering
Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
, particularly in signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, compressed sensing is the process of acquiring and reconstructing a signal that is supposed to be sparse
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
or compressible
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
.
History
Several scientific fields used L1Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
techniques. In statistics, the least-squares method was complemented by the
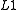-norm , which was introduced by Laplace. Following the introduction of linear programmingLinear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
and Dantzig's simplex algorithm
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
, the L1-norm was used in computational statistics
Computational statistics
Computational statistics, or statistical computing, is the interface between statistics and computer science. It is the area of computational science specific to the mathematical science of statistics....
. In statistical theory, the L1-norm was used by George W. Brown
George W. Brown
George William Brown was a Canadian politician and the second Lieutenant Governor of Saskatchewan from 1910 to 1915....
and later writers on median-unbiased estimators. It was used by Peter Huber and others working on robust statistics
Robust statistics
Robust statistics provides an alternative approach to classical statistical methods. The motivation is to produce estimators that are not unduly affected by small departures from model assumptions.- Introduction :...
. The
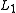norm was also used in signal processing, for example, in the 1970s, when seismologists constructed images of reflective layers within the earth based on data that did not seem to satisfy the Nyquist–Shannon criterionNyquist–Shannon sampling theorem
The Nyquist–Shannon sampling theorem, after Harry Nyquist and Claude Shannon, is a fundamental result in the field of information theory, in particular telecommunications and signal processing. Sampling is the process of converting a signal into a numeric sequence...
. It was used in matching pursuit
Matching pursuit
Matching pursuit is a type of numerical technique which involves finding the "best matching" projections of multidimensional data onto an over-complete dictionary D...
in 1993, the LASSO estimator by Robert Tibshirani
Robert Tibshirani
Robert Tibshirani is a Professor in the Departments of Statistics and Health Research and Policy at Stanford University. He was a Professor at the University of Toronto from 1985 to 1998. In his work, he develops statistical tools for the analysis of complex datasets, most recently in genomics and...
in 1996 and Basis Pursuit in 1998. There were theoretical results describing when these algorithms recovered sparse solutions, but the required type and number of measurements were sub-optimal and subsequently greatly improved by compressed sensing. Around 2004 Emmanuel Candès
Emmanuel Candès
Emmanuel Jean Candès is a professor of mathematics and statistics at Stanford University.-Academic biography:Candès earned a B.Sc. from the École Polytechnique in 1993. He did his graduate studies at Stanford, where he earned a Ph.D. in statistics in 1998 under the supervision of David Donoho and...
, Terence Tao
Terence Tao
Terence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
and David Donoho
David Donoho
David Leigh Donoho, born on March 5, 1957 in Los Angeles, is a professor of statistics at Stanford University, where he is also the Anne T. and Robert M. Bass Professor in the Humanities and Sciences...
discovered important results on the minimum number of data needed to reconstruct an image even though the number of data would be deemed insufficient by the Nyquist–Shannon criterion.
Underdetermined linear system
An underdetermined systemUnderdetermined system
In mathematics, a system of linear equations is considered underdetermined if there are fewer equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
of linear equations has more unknowns than equations and generally has an infinite number of solutions. However, if there is a unique sparse solution to the underdetermined system, then the Compressed Sensing framework allows the recovery of that solution. Not all underdetermined systems of linear equations have a sparse solution.
Solution / reconstruction method
Compressed sensing takes advantage of the redundancy in many of interesting signals—they are not pure noise. In particular, many signals are sparseSparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
, that is, they contain many coefficients close to or equal to zero, when represented in some domain. This is the same insight used in many forms of lossy compression.
Compressed sensing typically starts with taking a weighted linear combination of samples also called compressive measurements in a basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
different from the basis in which the signal is known to be sparse. The results found by David Donoho
David Donoho
David Leigh Donoho, born on March 5, 1957 in Los Angeles, is a professor of statistics at Stanford University, where he is also the Anne T. and Robert M. Bass Professor in the Humanities and Sciences...
, Emmanuel Candès
Emmanuel Candès
Emmanuel Jean Candès is a professor of mathematics and statistics at Stanford University.-Academic biography:Candès earned a B.Sc. from the École Polytechnique in 1993. He did his graduate studies at Stanford, where he earned a Ph.D. in statistics in 1998 under the supervision of David Donoho and...
, Justin Romberg and Terence Tao
Terence Tao
Terence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
showed that the number of these compressive measurements can be small and still contain nearly all the useful information. Therefore, the task of converting the image back into the intended domain involves solving an underdetermined
Underdetermined system
In mathematics, a system of linear equations is considered underdetermined if there are fewer equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
matrix equation since the number of compressive measurements taken is smaller than the number of pixels in the full image. However, adding the constraint that the initial signal is sparse enables one to solve this underdetermined
Underdetermined system
In mathematics, a system of linear equations is considered underdetermined if there are fewer equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
system of linear equations.
The least-squares solution to such problems is to minimize the
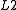norm—that is, minimize the amount of energy in the system. This is usually simple mathematically (involving only a matrix multiplicationMatrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
by the pseudo-inverse of the basis sampled in). However, this leads to poor results for many practical applications, for which the unknown coefficients have nonzero energy.
To enforce the sparsity constraint when solving for the underdetermined system of linear equations
Underdetermined system
In mathematics, a system of linear equations is considered underdetermined if there are fewer equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
, one can minimize the number of nonzero components of the solution.
The function counting the number of non-zero components of a vector was called the
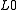"norm" by David Donoho. The quotation marks served two warnings. First, the number-of-nonzeros 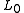-"norm" is not a proper F-normF-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
, because it is not continuous in its scalar argument: nnzs(αx) is constant as α approaches zero. Unfortunately, later authors have neglected Donoho's quotation marks and abused terminology—clashing with the established use of the
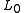norm for the space of measurable functions (equipped with an appropriate metric) or for the spaceF-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
of sequences with F–norm
F-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
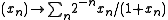. Candès
Emmanuel Candès
Emmanuel Jean Candès is a professor of mathematics and statistics at Stanford University.-Academic biography:Candès earned a B.Sc. from the École Polytechnique in 1993. He did his graduate studies at Stanford, where he earned a Ph.D. in statistics in 1998 under the supervision of David Donoho and...
. et. al., proved that for many problems it is probable that the
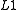norm is equivalent to the 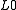norm, in a technical sense: This equivalence result allows one to solve the L1 problem, which is easier than the 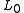problem. Finding the candidate with the smallest 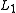norm can be expressed relatively easily as a linear program, for which efficient solution methods already exist. When measurements may contain a finite amount of noise, basis pursuit denoising is preferred over linear programming, since it preserves sparsity in the face of noise and can be solved faster than an exact linear program.Implementations
The field of compressive sensing is related to other topics in signal processing and computational mathematics, such as to underdetermined linear-systemUnderdetermined system
In mathematics, a system of linear equations is considered underdetermined if there are fewer equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
s, group testing
Group testing
In combinatorial mathematics, group testing is a set of problems with the objective of reducing the cost of identifying certain elements of a set.-Background:Robert Dorfman's paper in 1943 introduced the field of Group Testing...
, heavy hitters, sparse coding
Sparse coding
The sparse code is a kind of neural code in which each item is encoded by the strong activation of a relatively small set of neurons. For each item to be encoded, this is a different subset of all available neurons....
, multiplexing
Multiplexing
The multiplexed signal is transmitted over a communication channel, which may be a physical transmission medium. The multiplexing divides the capacity of the low-level communication channel into several higher-level logical channels, one for each message signal or data stream to be transferred...
, sparse sampling, and finite rate of innovation. Imaging techniques having a strong affinity with compressive sensing include coded aperture
Coded aperture
Coded Apertures or Coded-Aperture Masks are grids, gratings, or other patterns of materials opaque to various wavelengths of light. The wavelengths are usually high-energy radiation such as X-rays and gamma rays. By blocking and unblocking light in a known pattern, a coded "shadow" is cast upon a...
and computational photography
Computational photography
Computational imaging refers to any image formation method that involves a digital computer. Computational photography refers broadly to computational imaging techniques that enhance or extend the capabilities ofdigital photography...
.
Starting with the single-pixel camera from Rice University
Rice University
William Marsh Rice University, commonly referred to as Rice University or Rice, is a private research university located on a heavily wooded campus in Houston, Texas, United States...
, an up-to-date list of the most recent implementations of compressive sensing in hardware at different technology readiness level
Technology Readiness Level
Technology Readiness Level is a measure used by some United States government agencies and many of the world's major companies to assess the maturity of evolving technologies prior to incorporating that technology into a system or subsystem...
is available. Some hardware implementation (like the one used in MRI or compressed genotyping) do not require an actual physical change, whereas other hardware require substantial re-engineering to perform this new type of sampling. Similarly, a number of hardware implementations already existed before 2004; however, while they were acquiring signals in a compressed manner, they generally did not use compressive sensing reconstruction techniques to reconstruct the original signal. The result of these reconstruction were suboptimal and have been greatly enhanced thanks to compressive sensing.
Compressive sensing in the news
Compressed sensing was in the news as part of the single-pixel camera from Rice UniversityRice University
William Marsh Rice University, commonly referred to as Rice University or Rice, is a private research university located on a heavily wooded campus in Houston, Texas, United States...
. Some aspects of compressed sensing were featured in Wired's "Engineers Test Highly Accurate Face Recognition". A more recent article in Wired described compressed sensing as a full-fledged technique in "Using Math to Turn Lo-Res Datasets Into Hi-Res Samples". Because the article was talking about sampling for MRI, some confusion might have occurred.
Further reading
- Using Math to Turn Lo-Res Datasets Into Hi-Res Samples Wired Magazine article
- Compressive Sensing Resources at Rice UniversityRice UniversityWilliam Marsh Rice University, commonly referred to as Rice University or Rice, is a private research university located on a heavily wooded campus in Houston, Texas, United States...
. - Compressed Sensing: The Big Picture
- A list of different hardware implementation of Compressive Sensing
- Compressed Sensing 2.0
- Compressed Sensing Makes Every Pixel Count – article in the AMS What's Happening in the Mathematical Sciences series
- Nuit Blanche A blog on Compressive Sensing featuring the most recent information on the subject (preprints, presentations, Q/As)
- Online Talks focused on Compressive Sensing