
Compression body
Encyclopedia
In the theory of 3-manifold
s, a compression body is a kind of generalized handlebody
.
A compression body is either a handlebody
or the result of the following construction:
Compression bodies often arise when manipulating Heegaard splitting
s.
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
s, a compression body is a kind of generalized handlebody
Handlebody
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
.
A compression body is either a handlebody
Handlebody
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
or the result of the following construction:
- Let
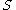 be a compact, closed surface (not necessarily connected). Attach 1- handles to
be a compact, closed surface (not necessarily connected). Attach 1- handles to 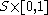 along
along  .
.
- Let
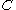 be a compression body.
be a compression body. - The negative boundary of C, denoted
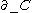 , is
, is 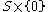 . (If
. (If  is a handlebody then
is a handlebody then 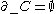 .) The positive boundary of C, denoted
.) The positive boundary of C, denoted 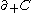 , is
, is 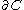 minus the negative boundary.
minus the negative boundary.
- There is a dual construction of compression bodies starting with a surface
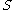 and attaching 2-handles to
and attaching 2-handles to  . In this case
. In this case  is
is 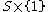 , and
, and  is
is 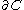 minus the positive boundary.
minus the positive boundary.
Compression bodies often arise when manipulating Heegaard splitting
Heegaard splitting
In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.-Definitions:...
s.

