
Heegaard splitting
Encyclopedia
In the mathematical
field of geometric topology
, a Heegaard splitting is a decomposition of a compact oriented 3-manifold
that results from dividing it into two handlebodies
.
of genus g, and let ƒ be an orientation reversing homeomorphism
from the boundary
of V to the boundary of W. By gluing V to W along ƒ we obtain the compact oriented 3-manifold

Every closed, orientable three-manifold may be so obtained; this follows from deep results on the triangulability of three-manifolds due to Moise
. This contrasts strongly with higher dimensional manifolds which need not admit smooth or piecewise linear structures.
The decomposition of M into two handlebodies is called a Heegaard splitting, and their common boundary H is called the Heegaard surface of the splitting. Splittings are considered up to isotopy.
The gluing map ƒ need only be specified up to taking a double coset
in the mapping class group
of H. This connection with the mapping class group was first made by W. B. R. Lickorish.
Heegaard splittings can also be defined for compact 3-manifolds with boundary by replacing handlebodies with compression bodies
. The gluing map is between the positive boundaries of the compression bodies.
A simple closed curve on a surface is essential if it is does not bound a disc on the surface.
A Heegaard splitting is reducible if there is an essential simple closed curve on H which bounds a disk in both V and in W. A splitting is irreducible if it is not reducible. It follows from Haken's Lemma that in a reducible manifold every splitting is reducible.
on H which bounds a disk in both V and in W. A splitting is irreducible if it is not reducible. It follows from Haken's Lemma that in a reducible manifold every splitting is reducible.
A Heegaard splitting is stabilized if there are essential simple closed curves and
and 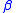 on H where
on H where  bounds a disk in V,
bounds a disk in V, 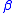 bounds a disk in W, and
bounds a disk in W, and  and
and 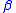 intersect exactly once. It follows from Waldhausen's Theorem that every reducible splitting of an irreducible manifold is stabilized.
intersect exactly once. It follows from Waldhausen's Theorem that every reducible splitting of an irreducible manifold is stabilized.
A Heegaard splitting is weakly reducible if there are disjoint essential simple closed curves and
and  on H where
on H where  bounds a disk in V and
bounds a disk in V and 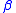 bounds a disk in W. A splitting is strongly irreducible if it is not weakly reducible.
bounds a disk in W. A splitting is strongly irreducible if it is not weakly reducible.
A Heegaard splitting is minimal or minimal genus if there is no other splitting of the ambient three-manifold of lower genus
. The minimal value g of the splitting surface is the Heegaard genus of M.
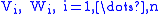 and surfaces
and surfaces 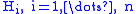 such that
such that 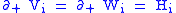 and
and  . The interiors of the compression bodies must be pairwise disjoint and their union must be all of
. The interiors of the compression bodies must be pairwise disjoint and their union must be all of  . The surface
. The surface 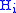 forms a Heegaard surface for the submanifold
forms a Heegaard surface for the submanifold 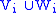 of
of  . (Note that here each Vi and Wi is allowed to have more than one component.)
. (Note that here each Vi and Wi is allowed to have more than one component.)
A generalized Heegaard splitting is called strongly irreducible if each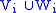 is strongly irreducible.
is strongly irreducible.
There is an analogous notion of thin position, defined for knots, for Heegaard splittings. The complexity of a connected surface S, c(S), is defined to be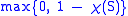 ; the complexity of a disconnected surface is the sum of complexities of its components. The complexity of a generalized Heegaard splitting is the multi-set {c(S_i)}, where the index runs over the Heegaard surfaces in the generalized splitting. These multi-sets can be well-ordered by lexicographical ordering (monotonically decreasing). A generalized Heegaard splitting is thin if its complexity is minimal.
; the complexity of a disconnected surface is the sum of complexities of its components. The complexity of a generalized Heegaard splitting is the multi-set {c(S_i)}, where the index runs over the Heegaard surfaces in the generalized splitting. These multi-sets can be well-ordered by lexicographical ordering (monotonically decreasing). A generalized Heegaard splitting is thin if its complexity is minimal.
 is the set of vectors in
is the set of vectors in 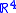 with length one. Intersecting this with the
with length one. Intersecting this with the  hyperplane gives a two-sphere. This is the standard genus zero splitting of
hyperplane gives a two-sphere. This is the standard genus zero splitting of 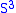 . Conversely, by Alexander's Trick, all manifolds admitting a genus zero splitting are homeomorphic to
. Conversely, by Alexander's Trick, all manifolds admitting a genus zero splitting are homeomorphic to 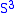 .
.
Under the usual identification of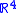 with
with 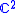 we may view
we may view 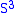 as living in
as living in 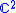 . Then the set of points where each coordinate has norm
. Then the set of points where each coordinate has norm 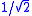 forms a Clifford torus
forms a Clifford torus
,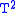 . This is the standard genus one splitting of
. This is the standard genus one splitting of 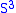 . (See also the discussion at Hopf bundle
. (See also the discussion at Hopf bundle
.)
Stabilization: Given an Heegaard splitting H in M the stabilization of H is formed by taking the connected sum
of the pair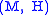 with the pair
with the pair 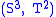 . It is easy to show that the stabilization procedure yields stabilized splittings. Inductively, a splitting is standard if it is the stabilization of a standard splitting.
. It is easy to show that the stabilization procedure yields stabilized splittings. Inductively, a splitting is standard if it is the stabilization of a standard splitting.
Lens space
s: All have a standard splitting of genus one. This is the image of the Clifford torus in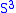 under the quotient map used to define the lens space in question. It follows from the structure of the mapping class group
under the quotient map used to define the lens space in question. It follows from the structure of the mapping class group
of the two-torus
that only lens spaces have splittings of genus one.
Three-torus: Recall that the three-torus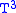 is the Cartesian product
is the Cartesian product
of three copies of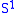 (circle
(circle
s). Let be a point of
be a point of 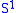 and consider the graph
and consider the graph
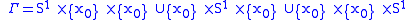 . It is an easy exercise to show that V, a regular neighborhood of
. It is an easy exercise to show that V, a regular neighborhood of  , is a handlebody as is
, is a handlebody as is  . Thus the boundary of V in
. Thus the boundary of V in 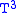 is a Heegaard splitting and this is the standard splitting of
is a Heegaard splitting and this is the standard splitting of 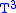 . It was proved by Frohman and Hass that any other genus 3 Heegaard splitting of the three-torus is topologically
. It was proved by Frohman and Hass that any other genus 3 Heegaard splitting of the three-torus is topologically
equivalent to this one. Boileau and Otal proved that in general any Heegaard splitting of the three-torus is equivalent to the result of stabilizing this example.
.) This may be restated as follows: the genus zero splitting of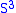 is unique.
is unique.
Waldhausen's Theorem: Every splitting of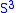 is obtained by stabilizing the unique splitting of genus zero.
is obtained by stabilizing the unique splitting of genus zero.
Suppose now that M is a closed orientable three-manifold.
Reidemeister-Singer Theorem: For any pair of splittings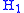 and
and 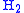 in M there is a third splitting
in M there is a third splitting  in M which is a stabilization of both.
in M which is a stabilization of both.
Haken's Lemma: Suppose that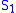 is an essential two-sphere in M and H is a Heegaard splitting. Then there is an essential two-sphere
is an essential two-sphere in M and H is a Heegaard splitting. Then there is an essential two-sphere 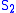 in M meeting H in a single curve.
in M meeting H in a single curve.
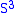 are standard. The same holds for lens space
are standard. The same holds for lens space
s (as proved by Francis Bonahon and J.P. Otal).
Splittings of Seifert fiber space
s are more subtle. Here, all splittings may be isotoped to be vertical or horizontal (as proved by Yoav Moriah and Jennifer Schultens).
classified splittings of torus bundle
s (which includes all three-manifolds with Sol geometry). It follows from their work that all torus bundles have a unique splitting of minimal genus. All other splittings of the torus bundle are stabilizations of the minimal genus one.
As of 2008, the only hyperbolic
three-manifolds whose Heegaard splittings are classified are two-bridge knot complements, in a paper of Tsuyoshi Kobayashi.
s first in the work of Blaine Lawson who proved that embedded minimal surfaces in compact manifolds of positive sectional curvature are Heegaard splittings. This result was extended by William Meeks to flat manifolds, except he proves that an embedded minimal surface in a flat three-manifold is either a Heegaard surface or totally geodesic.
Meeks and S. T. Yau went on to use results of Waldhausen to prove results about the topological uniqueness of minimal surface of finite topology in . The final topological classification of embedded minimal surfaces in
. The final topological classification of embedded minimal surfaces in 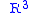 was given by Meeks and Frohman. The result relied heavily on techniques developed for studying the topology of Heegaard splittings.
was given by Meeks and Frohman. The result relied heavily on techniques developed for studying the topology of Heegaard splittings.
and Zoltán Szabó
. The theory uses the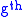 symmetric product of a Heegaard surface as the ambient space, and tori built from the boundaries of meridian disks for the two handlebodies as the Lagrangian submanifolds.
symmetric product of a Heegaard surface as the ambient space, and tori built from the boundaries of meridian disks for the two handlebodies as the Lagrangian submanifolds.
and Friedhelm Waldhausen
in the 1960s, it was not until a few decades later that the field was rejuvenated by , primarily through their concept of strong irreducibility.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
, a Heegaard splitting is a decomposition of a compact oriented 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
that results from dividing it into two handlebodies
Handlebody
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
.
Definitions
Let V and W be handlebodiesHandlebody
In the mathematical field of geometric topology, a handlebody is a decomposition of a manifold into standard pieces. Handlebodies play an important role in Morse theory, cobordism theory and the surgery theory of high-dimensional manifolds...
of genus g, and let ƒ be an orientation reversing homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
from the boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of V to the boundary of W. By gluing V to W along ƒ we obtain the compact oriented 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...

Every closed, orientable three-manifold may be so obtained; this follows from deep results on the triangulability of three-manifolds due to Moise
Edwin E. Moise
Edwin Evariste Moise was an American mathematician and mathematics education reformer. After his retirement from mathematics he became a literary critic of 19th century English poetry and had several notes published in that field.-Early life and education:...
. This contrasts strongly with higher dimensional manifolds which need not admit smooth or piecewise linear structures.
The decomposition of M into two handlebodies is called a Heegaard splitting, and their common boundary H is called the Heegaard surface of the splitting. Splittings are considered up to isotopy.
The gluing map ƒ need only be specified up to taking a double coset
Coset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
in the mapping class group
Mapping class group
In mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
of H. This connection with the mapping class group was first made by W. B. R. Lickorish.
Heegaard splittings can also be defined for compact 3-manifolds with boundary by replacing handlebodies with compression bodies
Compression body
In the theory of 3-manifolds, a compression body is a kind of generalized handlebody.A compression body is either a handlebody or the result of the following construction:Compression bodies often arise when manipulating Heegaard splittings....
. The gluing map is between the positive boundaries of the compression bodies.
A simple closed curve on a surface is essential if it is does not bound a disc on the surface.
A Heegaard splitting is reducible if there is an essential simple closed curve
 on H which bounds a disk in both V and in W. A splitting is irreducible if it is not reducible. It follows from Haken's Lemma that in a reducible manifold every splitting is reducible.
on H which bounds a disk in both V and in W. A splitting is irreducible if it is not reducible. It follows from Haken's Lemma that in a reducible manifold every splitting is reducible.A Heegaard splitting is stabilized if there are essential simple closed curves
 and
and 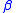 on H where
on H where  bounds a disk in V,
bounds a disk in V, 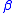 bounds a disk in W, and
bounds a disk in W, and  and
and 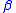 intersect exactly once. It follows from Waldhausen's Theorem that every reducible splitting of an irreducible manifold is stabilized.
intersect exactly once. It follows from Waldhausen's Theorem that every reducible splitting of an irreducible manifold is stabilized.A Heegaard splitting is weakly reducible if there are disjoint essential simple closed curves
 and
and  on H where
on H where  bounds a disk in V and
bounds a disk in V and 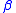 bounds a disk in W. A splitting is strongly irreducible if it is not weakly reducible.
bounds a disk in W. A splitting is strongly irreducible if it is not weakly reducible.A Heegaard splitting is minimal or minimal genus if there is no other splitting of the ambient three-manifold of lower genus
Genus
In biology, a genus is a low-level taxonomic rank used in the biological classification of living and fossil organisms, which is an example of definition by genus and differentia...
. The minimal value g of the splitting surface is the Heegaard genus of M.
Generalized Heegaard splittings
A generalized Heegaard splitting of M is a decomposition into compression bodiesCompression body
In the theory of 3-manifolds, a compression body is a kind of generalized handlebody.A compression body is either a handlebody or the result of the following construction:Compression bodies often arise when manipulating Heegaard splittings....
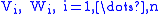 and surfaces
and surfaces 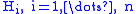 such that
such that 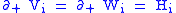 and
and  . The interiors of the compression bodies must be pairwise disjoint and their union must be all of
. The interiors of the compression bodies must be pairwise disjoint and their union must be all of  . The surface
. The surface 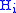 forms a Heegaard surface for the submanifold
forms a Heegaard surface for the submanifold 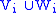 of
of  . (Note that here each Vi and Wi is allowed to have more than one component.)
. (Note that here each Vi and Wi is allowed to have more than one component.)A generalized Heegaard splitting is called strongly irreducible if each
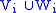 is strongly irreducible.
is strongly irreducible.There is an analogous notion of thin position, defined for knots, for Heegaard splittings. The complexity of a connected surface S, c(S), is defined to be
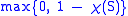 ; the complexity of a disconnected surface is the sum of complexities of its components. The complexity of a generalized Heegaard splitting is the multi-set {c(S_i)}, where the index runs over the Heegaard surfaces in the generalized splitting. These multi-sets can be well-ordered by lexicographical ordering (monotonically decreasing). A generalized Heegaard splitting is thin if its complexity is minimal.
; the complexity of a disconnected surface is the sum of complexities of its components. The complexity of a generalized Heegaard splitting is the multi-set {c(S_i)}, where the index runs over the Heegaard surfaces in the generalized splitting. These multi-sets can be well-ordered by lexicographical ordering (monotonically decreasing). A generalized Heegaard splitting is thin if its complexity is minimal.Examples
Three-sphere: The three-sphere is the set of vectors in
is the set of vectors in 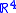 with length one. Intersecting this with the
with length one. Intersecting this with the  hyperplane gives a two-sphere. This is the standard genus zero splitting of
hyperplane gives a two-sphere. This is the standard genus zero splitting of 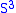 . Conversely, by Alexander's Trick, all manifolds admitting a genus zero splitting are homeomorphic to
. Conversely, by Alexander's Trick, all manifolds admitting a genus zero splitting are homeomorphic to 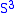 .
.Under the usual identification of
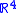 with
with 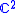 we may view
we may view 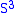 as living in
as living in 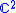 . Then the set of points where each coordinate has norm
. Then the set of points where each coordinate has norm 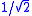 forms a Clifford torus
forms a Clifford torusClifford torus
In geometric topology, the Clifford torus is a special kind of torus sitting inside R4. Alternatively, it can be seen as a torus sitting inside C2 since C2 is topologically the same space as R4...
,
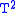 . This is the standard genus one splitting of
. This is the standard genus one splitting of 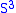 . (See also the discussion at Hopf bundle
. (See also the discussion at Hopf bundleHopf bundle
In the mathematical field of topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle...
.)
Stabilization: Given an Heegaard splitting H in M the stabilization of H is formed by taking the connected sum
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
of the pair
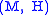 with the pair
with the pair 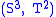 . It is easy to show that the stabilization procedure yields stabilized splittings. Inductively, a splitting is standard if it is the stabilization of a standard splitting.
. It is easy to show that the stabilization procedure yields stabilized splittings. Inductively, a splitting is standard if it is the stabilization of a standard splitting.Lens space
Lens space
A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
s: All have a standard splitting of genus one. This is the image of the Clifford torus in
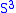 under the quotient map used to define the lens space in question. It follows from the structure of the mapping class group
under the quotient map used to define the lens space in question. It follows from the structure of the mapping class groupMapping class group
In mathematics, in the sub-field of geometric topology, the mapping class groupis an important algebraic invariant of a topological space. Briefly, the mapping class group is a discrete group of 'symmetries' of the space.-Motivation:...
of the two-torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
that only lens spaces have splittings of genus one.
Three-torus: Recall that the three-torus
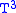 is the Cartesian product
is the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of three copies of
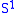 (circle
(circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s). Let
 be a point of
be a point of 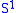 and consider the graph
and consider the graph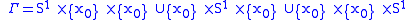 . It is an easy exercise to show that V, a regular neighborhood of
. It is an easy exercise to show that V, a regular neighborhood of  , is a handlebody as is
, is a handlebody as is  . Thus the boundary of V in
. Thus the boundary of V in 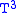 is a Heegaard splitting and this is the standard splitting of
is a Heegaard splitting and this is the standard splitting of 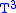 . It was proved by Frohman and Hass that any other genus 3 Heegaard splitting of the three-torus is topologically
. It was proved by Frohman and Hass that any other genus 3 Heegaard splitting of the three-torus is topologicallyequivalent to this one. Boileau and Otal proved that in general any Heegaard splitting of the three-torus is equivalent to the result of stabilizing this example.
Theorems
Alexander's Lemma: Up to isotopy, there is a unique (piecewise linear) embedding of the two-sphere into the three-sphere. (In higher dimensions this is known as the Schoenflies theorem. In dimension two this is the Jordan curve theoremJordan curve theorem
In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...
.) This may be restated as follows: the genus zero splitting of
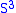 is unique.
is unique.Waldhausen's Theorem: Every splitting of
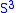 is obtained by stabilizing the unique splitting of genus zero.
is obtained by stabilizing the unique splitting of genus zero.Suppose now that M is a closed orientable three-manifold.
Reidemeister-Singer Theorem: For any pair of splittings
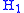 and
and 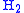 in M there is a third splitting
in M there is a third splitting  in M which is a stabilization of both.
in M which is a stabilization of both.Haken's Lemma: Suppose that
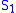 is an essential two-sphere in M and H is a Heegaard splitting. Then there is an essential two-sphere
is an essential two-sphere in M and H is a Heegaard splitting. Then there is an essential two-sphere 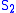 in M meeting H in a single curve.
in M meeting H in a single curve.Classifications
There are several classes of three-manifolds where the set of Heegaard splittings is completely known. For example, Waldhausen's Theorem shows that all splittings of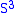 are standard. The same holds for lens space
are standard. The same holds for lens spaceLens space
A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
s (as proved by Francis Bonahon and J.P. Otal).
Splittings of Seifert fiber space
Seifert fiber space
A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...
s are more subtle. Here, all splittings may be isotoped to be vertical or horizontal (as proved by Yoav Moriah and Jennifer Schultens).
classified splittings of torus bundle
Torus bundle
In mathematics, in the sub-field of geometric topology, a torus bundle is a kind of surface bundle over the circle, which in turn are a class of three-manifolds.-Construction:To obtain a torus bundle: let f be an...
s (which includes all three-manifolds with Sol geometry). It follows from their work that all torus bundles have a unique splitting of minimal genus. All other splittings of the torus bundle are stabilizations of the minimal genus one.
As of 2008, the only hyperbolic
Geometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
three-manifolds whose Heegaard splittings are classified are two-bridge knot complements, in a paper of Tsuyoshi Kobayashi.
Minimal surfaces
Heegaard splittings appeared in the theory of minimal surfaceMinimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
s first in the work of Blaine Lawson who proved that embedded minimal surfaces in compact manifolds of positive sectional curvature are Heegaard splittings. This result was extended by William Meeks to flat manifolds, except he proves that an embedded minimal surface in a flat three-manifold is either a Heegaard surface or totally geodesic.
Meeks and S. T. Yau went on to use results of Waldhausen to prove results about the topological uniqueness of minimal surface of finite topology in
 . The final topological classification of embedded minimal surfaces in
. The final topological classification of embedded minimal surfaces in 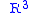 was given by Meeks and Frohman. The result relied heavily on techniques developed for studying the topology of Heegaard splittings.
was given by Meeks and Frohman. The result relied heavily on techniques developed for studying the topology of Heegaard splittings.Heegaard Floer homology
Heegaard diagrams, which are simple combinatorial descriptions of Heegaard splittings, have been used extensively to construct invariants of three-manifolds. The most recent example of this is the Heegaard Floer homology of Peter OzsvathPeter Ozsváth
Peter Steven Ozsváth is a professor of mathematics at Princeton University. He created, along with Zoltán Szabó, Heegaard Floer homology, a homology theory for 3-manifolds....
and Zoltán Szabó
Zoltán Szabó
Zoltán Szabó is a professor of mathematics at Princeton University. He created, along with Peter Ozsváth, Heegaard Floer homology, a homology theory for 3-manifolds. For this contribution to the field of topology, Ozsváth and Szabó were awarded the 2007 Oswald Veblen Prize in Geometry.He got his...
. The theory uses the
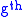 symmetric product of a Heegaard surface as the ambient space, and tori built from the boundaries of meridian disks for the two handlebodies as the Lagrangian submanifolds.
symmetric product of a Heegaard surface as the ambient space, and tori built from the boundaries of meridian disks for the two handlebodies as the Lagrangian submanifolds.History
The idea of a Heegaard splitting was introduced by . While Heegaard splittings were studied extensively by mathematicians such as Wolfgang HakenWolfgang Haken
Wolfgang Haken is a mathematician who specializes in topology, in particular 3-manifolds.In 1976 together with colleague Kenneth Appel at the University of Illinois at Urbana-Champaign, Haken solved one of the most famous problems in mathematics, the four-color theorem...
and Friedhelm Waldhausen
Friedhelm Waldhausen
Friedhelm Waldhausen is a German mathematician known for his work in algebraic topology.-Academic life:...
in the 1960s, it was not until a few decades later that the field was rejuvenated by , primarily through their concept of strong irreducibility.

