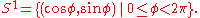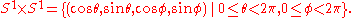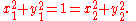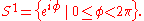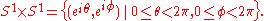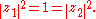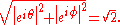Clifford torus
Encyclopedia
In geometric topology
, the Clifford torus is a special kind of torus
sitting inside R4. Alternatively, it can be seen as a torus sitting inside C2 since C2 is topologically the same space as R4. Furthermore, every point of the Clifford torus lies at a fixed distance from the origin; therefore, it can also be viewed as sitting inside a 3-sphere
.
The Clifford torus is also known as a square torus, because it is isometric
to a square
with side length 2π and with opposite sides identified.
S1 in R2 can be parameterized by an angle coordinate:
In another copy of R2, take another copy of the unit circle
Then the Clifford torus is
Since each copy of S1 is an embedded submanifold
of R2, the Clifford torus is an embedded torus in R2 × R2 = R4.
If R4 is given by coordinates (x1, y1, x2, y2), then the Clifford torus is given by
torus in C2. In two copies of C, we have the following unit circles (still parametrized by an angle coordinate):
and
Now the Clifford torus appears as
As before, this is an embedded submanifold, in this case of C2.
If C2 is given by coordinates (z1, z2), then the Clifford torus is given by
In the Clifford torus as defined above, the distance of any point of the Clifford torus to the origin of C2 is
The set of all points at a distance of √2 from the origin of C2 is a 3-sphere, and so the Clifford torus sits inside this 3-sphere. In fact, the Clifford torus divides this 3-sphere into two congruent solid tori
. (See Heegaard splitting
.)
Instead of defining the Clifford torus as the product of two unit circles, it is also common to use two circles of radius 1/√2. (For example, Paul Norbury uses this convention when describing the Lawson Conjecture.) With the alternate radius of 1/√2, the Clifford torus instead sits in the unit 3-sphere S3.
Since O(4)
acts on R4 by orthogonal transformations, we can move the "standard" Clifford torus defined above to other equivalent tori via rigid rotations. The six-dimensional group O(4) acts transitively on the space of all such Clifford tori sitting inside the 3-sphere. However, this action has a two-dimensional stabilizer (see group action
) since rotation in the meridional and longitudinal directions of a torus preserves the torus (as opposed to moving it to a different torus). So there is actually a four-dimensional space of Clifford tori.
The Lawson (or Hsiang–Lawson) conjecture states that every minimally embedded
torus in the 3-sphere with the round metric must be a Clifford torus.
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
, the Clifford torus is a special kind of torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
sitting inside R4. Alternatively, it can be seen as a torus sitting inside C2 since C2 is topologically the same space as R4. Furthermore, every point of the Clifford torus lies at a fixed distance from the origin; therefore, it can also be viewed as sitting inside a 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
.
The Clifford torus is also known as a square torus, because it is isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
to a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
with side length 2π and with opposite sides identified.
Formal definition
The unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
S1 in R2 can be parameterized by an angle coordinate:
In another copy of R2, take another copy of the unit circle
Then the Clifford torus is
Since each copy of S1 is an embedded submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of R2, the Clifford torus is an embedded torus in R2 × R2 = R4.
If R4 is given by coordinates (x1, y1, x2, y2), then the Clifford torus is given by
Alternate definitions
It is also common to consider the Clifford torus as an embeddedEmbedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
torus in C2. In two copies of C, we have the following unit circles (still parametrized by an angle coordinate):
and
Now the Clifford torus appears as
As before, this is an embedded submanifold, in this case of C2.
If C2 is given by coordinates (z1, z2), then the Clifford torus is given by
In the Clifford torus as defined above, the distance of any point of the Clifford torus to the origin of C2 is
The set of all points at a distance of √2 from the origin of C2 is a 3-sphere, and so the Clifford torus sits inside this 3-sphere. In fact, the Clifford torus divides this 3-sphere into two congruent solid tori
Solid torus
In mathematics, a solid torus is a topological space homeomorphic to S^1 \times D^2, i.e. the cartesian product of the circle with a two dimensional disc endowed with the product topology. The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary...
. (See Heegaard splitting
Heegaard splitting
In the mathematical field of geometric topology, a Heegaard splitting is a decomposition of a compact oriented 3-manifold that results from dividing it into two handlebodies.-Definitions:...
.)
Instead of defining the Clifford torus as the product of two unit circles, it is also common to use two circles of radius 1/√2. (For example, Paul Norbury uses this convention when describing the Lawson Conjecture.) With the alternate radius of 1/√2, the Clifford torus instead sits in the unit 3-sphere S3.
Since O(4)
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
acts on R4 by orthogonal transformations, we can move the "standard" Clifford torus defined above to other equivalent tori via rigid rotations. The six-dimensional group O(4) acts transitively on the space of all such Clifford tori sitting inside the 3-sphere. However, this action has a two-dimensional stabilizer (see group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
) since rotation in the meridional and longitudinal directions of a torus preserves the torus (as opposed to moving it to a different torus). So there is actually a four-dimensional space of Clifford tori.
Uses in mathematics
In symplectic geometry, the Clifford torus gives an example of an embedded Lagrangian submanifold of C2 with the standard symplectic structure. (Of course, any product of embedded circles in C gives a Lagrangian torus of C2, so these need not be Clifford tori.)The Lawson (or Hsiang–Lawson) conjecture states that every minimally embedded
Minimal surface
In mathematics, a minimal surface is a surface with a mean curvature of zero.These include, but are not limited to, surfaces of minimum area subject to various constraints....
torus in the 3-sphere with the round metric must be a Clifford torus.