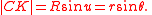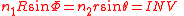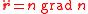Computation of radiowave attenuation in the atmosphere
Encyclopedia
One of the causes of attenuation of radio propagation
is the absorption
by the atmosphere
. There are many well known facts on the phenomenon and qualitative treatments in textbook
s. A document published by the International Telecommunication Union
(ITU)
provides some basis for a quantitative assessment of the attenuation. That document describes a simplified model along with semi-empirical formulas based on data fitting. It also recommended an algorithm
to compute the attenuation of radiowave propagation in the atmosphere. NASA
also published a study on a related subject. Free software based on ITU-R recommendations of the French Spatial Reasearches Institute CNES for download is also available to the public.
section considers the atmosphere as being divided into spherical homogeneous layers; each layer has a constant refraction index. By the use of trigonometry
, a couple of formulas and an algorithm were derived.
Through the use of an invariant
, the same results can be directly derived:
An incident ray at A under the angle Φ hits the layer B at the angle θ. From basic Euclidean geometry
:
By Snell's law
(or René Descartes
' law from the French point of view!) :
so that
Notes:
The ITU recommended algorithm consists of launching a ray from a radio source
, then at each step, a layer is chosen and a new incidence angle is then computed. The process is iterated until the altitude of the target is reached. At each step, the covered distance dL is multiplied by a specific attenuation coefficient
g expressed in dB/km. All the increments g dL are added to provide the total attenuation.
Note that the algorithm does not guaranty that the target is actually reached. For this, a much harder boundary value problem
would have to be solved.
can be considered. Usually the equation is presented under the self-adjoint form, a more tractable equation for the ray head position vector r is given in generic parametric form:
The first two are only of 1st order approximation (see Orders of approximation
). For the eikonal equation
, many numerical schemes are available. Here only a simple second order scheme was chosen. For most standard configurations of source-target, the three methods differ little from each other. It is only in the case of rays grazing the ground that the differences are meaningful. The following was used for testing:
At the latitude of 10o, when a ray starts at 5 km altitude with an elevation angle of −1o to hit a target at the same longitude but at latitude 8.84o and altitude 30 km. At 22.5 GHz, the results are:
Note that 22.5 GHz is not a practical frequency but it is the most suitable for algorithms comparison. In the table, the first column gives the results in dB, the third gives the distance covered and the last gives the final altitude. Distances are in km. From the altitude 30 km up, the attenuation is negligible. The paths of the three are plotted:
The linear path is the highest on the figure, the eikonal is the lowest.
Note: A MATLAB
version for the uplink (Telecommunications link) is available from the ITU
For the Eikonal equation, this correction can be done by solving a boundary value problem
. As the equation is of second order, the problem is well defined. In spite of the lack of a firm theoretical basis for the ITU method, a trial-error by dichotomy (or binary search
) can also be used. The next figure shows the results of numerical simulations.
The curve labeled as bvp is the trajectory found by correcting the elevation angle. The other two are from a fix step and a variable steps (chosen in accordance to the ITU recommendations) solutions without the elevation angle correction. The nominal elevation angle for this case is -0.5 degree. The numerical results obtained at 22.5 GHz were:
Note the way the solution bvp bents over the straight line. A consequence of this property is that the ray can reach locations situated below the horizon of S. This is consistent with observations. The trajectory is a Concave function
is a consequence of the fact that the gradient of the refraction index is negative, so the Eikonal equation implies that the second derivative of the trajectory is negative. From the point where the ray is parallel to ground, relative to the chosen coordinates, the ray goes down but relative to ground level, the ray goes up.
Often engineers are interested in finding the limits of a system. In this case, a simple idea is to try some low elevation angle and let the ray reach the desired altitude. This point of view has a problem: if suffice to take the angle for which the ray has a tangent point of lowest altitude. For instance with the case of a source at 5 km altitude, of nominal elevation angle -0.5 degree and the target is at 30 km altitude; the attenuation found by the boundary value method is 11.33 dB. The previous point of view of worst case leads to an elevation angle of -1.87 degree and an attenuation of 170.77 dB. With this kind of attenuation, every system would be unusable! It was found also for this case that with the nominal elevation angle, the distance of the tangent point to ground is 5.84 km; that of the worst case is 2.69 km. The nominal distance from source to target is 6383.84 km; for the worst case, it is 990.36 km.
There are many numerical methods to solve boundary value problems. For the Eikonal equation, due the good behavior of the refraction index just a simple Shooting method
can be used.
The attenuation mechanism as described here is only one amongst many others others. The full problem is much more complex.
Radio propagation
Radio propagation is the behavior of radio waves when they are transmitted, or propagated from one point on the Earth to another, or into various parts of the atmosphere...
is the absorption
Absorption
Absorption may refer to:- Chemistry and biology :* Absorption , absorption of particles of gas or liquid in liquid or solid material* Absorption , a route by which substances can enter the body through the skin...
by the atmosphere
Atmosphere
An atmosphere is a layer of gases that may surround a material body of sufficient mass, and that is held in place by the gravity of the body. An atmosphere may be retained for a longer duration, if the gravity is high and the atmosphere's temperature is low...
. There are many well known facts on the phenomenon and qualitative treatments in textbook
Textbook
A textbook or coursebook is a manual of instruction in any branch of study. Textbooks are produced according to the demands of educational institutions...
s. A document published by the International Telecommunication Union
International Telecommunication Union
The International Telecommunication Union is the specialized agency of the United Nations which is responsible for information and communication technologies...
(ITU)
provides some basis for a quantitative assessment of the attenuation. That document describes a simplified model along with semi-empirical formulas based on data fitting. It also recommended an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to compute the attenuation of radiowave propagation in the atmosphere. NASA
NASA
The National Aeronautics and Space Administration is the agency of the United States government that is responsible for the nation's civilian space program and for aeronautics and aerospace research...
also published a study on a related subject. Free software based on ITU-R recommendations of the French Spatial Reasearches Institute CNES for download is also available to the public.
The model and the ITU recommendation
The document ITU-R P.676-8 of the ITU-RITU-R
The ITU Radiocommunication Sector is one of the three sectors of the International Telecommunication Union and is responsible for radio communication....
section considers the atmosphere as being divided into spherical homogeneous layers; each layer has a constant refraction index. By the use of trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, a couple of formulas and an algorithm were derived.
Through the use of an invariant
Invariant
Invariant and invariance may have several meanings, among which are:- Computer science :* Invariant , an Expression whose value doesn't change during program execution* A type in overriding that is neither covariant nor contravariant...
, the same results can be directly derived:
An incident ray at A under the angle Φ hits the layer B at the angle θ. From basic Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
:
By Snell's law
Snell's law
In optics and physics, Snell's law is a formula used to describe the relationship between the angles of incidence and refraction, when referring to light or other waves passing through a boundary between two different isotropic media, such as water and glass...
(or René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
' law from the French point of view!) :
so that
Notes:
- One proof starts from the Fermat's principleFermat's principleIn optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light...
. As a result one gets the proof of the Snell’s law along with this invariance. This invariant is valid in a more general situation; the spherical radius is then replaced by the Radius of curvatureRadius of curvature (mathematics)In geometry, the radius of curvature, R, of a curve at a point is a measure of the radius of the circular arc which best approximates the curve at that point. If this value taken to be positive when the curve turns anticlockwise and negative when the curve turns clockwise...
at points along the ray. It is also used in equation (4) of the 2005 NASA's report in an application of satellite tracking.
- The assumption of the refraction index varying with the latitude is not strictly compatible with the notion of layers. However the variation of the index is very small, this point is usually ignored in practice.
The ITU recommended algorithm consists of launching a ray from a radio source
Radio source
Radio sources are objects in outer space that emit strong radio waves. Radio emission comes from a wide variety of sources. Such objects represent some of the most extreme and energetic physical processes in the universe.-History:...
, then at each step, a layer is chosen and a new incidence angle is then computed. The process is iterated until the altitude of the target is reached. At each step, the covered distance dL is multiplied by a specific attenuation coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
g expressed in dB/km. All the increments g dL are added to provide the total attenuation.
Note that the algorithm does not guaranty that the target is actually reached. For this, a much harder boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
would have to be solved.
The eikonal equation
This equation is discussed in the references. The equation is highly non-linear. Given that a smooth data fitting curve n(altitude) is provided by the ITU for the refraction index n, and that the values of n differs from 1 only by something of the order 10−4, a numerical solution of the eikonal equationEikonal equation
The eikonal equation is a non-linear partial differential equation encountered in problems of wave propagation, when the wave equation is approximated using the WKB theory...
can be considered. Usually the equation is presented under the self-adjoint form, a more tractable equation for the ray head position vector r is given in generic parametric form:
Implementations
Three implementations to compute the attenuations exist:- Take the ray to be a straight line.
- Use the optical invariant and apply the ITU recommendationITU.
- Solve the eikonal equation.
The first two are only of 1st order approximation (see Orders of approximation
Orders of approximation
In science, engineering, and other quantitative disciplines, orders of approximation refer to formal or informal terms for how precise an approximation is, and to indicate progressively more refined approximations: in increasing order of precision, a zeroth order approximation, a first order...
). For the eikonal equation
Eikonal equation
The eikonal equation is a non-linear partial differential equation encountered in problems of wave propagation, when the wave equation is approximated using the WKB theory...
, many numerical schemes are available. Here only a simple second order scheme was chosen. For most standard configurations of source-target, the three methods differ little from each other. It is only in the case of rays grazing the ground that the differences are meaningful. The following was used for testing:
At the latitude of 10o, when a ray starts at 5 km altitude with an elevation angle of −1o to hit a target at the same longitude but at latitude 8.84o and altitude 30 km. At 22.5 GHz, the results are:
Note that 22.5 GHz is not a practical frequency but it is the most suitable for algorithms comparison. In the table, the first column gives the results in dB, the third gives the distance covered and the last gives the final altitude. Distances are in km. From the altitude 30 km up, the attenuation is negligible. The paths of the three are plotted:
The linear path is the highest on the figure, the eikonal is the lowest.
Note: A MATLAB
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
version for the uplink (Telecommunications link) is available from the ITU
The boundary value problem
When a point S communicates with a point T, the orientation of the ray is specified by an elevation angle. In a naïve way, the angle can be given by tracing a straight line from S to T. This specification does not guaranty that the ray will reach T: the variation of refraction index bends the ray trajectory. The elevation angle has to be modified to take into account the bending effect.For the Eikonal equation, this correction can be done by solving a boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
. As the equation is of second order, the problem is well defined. In spite of the lack of a firm theoretical basis for the ITU method, a trial-error by dichotomy (or binary search
Binary search algorithm
In computer science, a binary search or half-interval search algorithm finds the position of a specified value within a sorted array. At each stage, the algorithm compares the input key value with the key value of the middle element of the array. If the keys match, then a matching element has been...
) can also be used. The next figure shows the results of numerical simulations.
The curve labeled as bvp is the trajectory found by correcting the elevation angle. The other two are from a fix step and a variable steps (chosen in accordance to the ITU recommendations) solutions without the elevation angle correction. The nominal elevation angle for this case is -0.5 degree. The numerical results obtained at 22.5 GHz were:
Note the way the solution bvp bents over the straight line. A consequence of this property is that the ray can reach locations situated below the horizon of S. This is consistent with observations. The trajectory is a Concave function
Concave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
is a consequence of the fact that the gradient of the refraction index is negative, so the Eikonal equation implies that the second derivative of the trajectory is negative. From the point where the ray is parallel to ground, relative to the chosen coordinates, the ray goes down but relative to ground level, the ray goes up.
Often engineers are interested in finding the limits of a system. In this case, a simple idea is to try some low elevation angle and let the ray reach the desired altitude. This point of view has a problem: if suffice to take the angle for which the ray has a tangent point of lowest altitude. For instance with the case of a source at 5 km altitude, of nominal elevation angle -0.5 degree and the target is at 30 km altitude; the attenuation found by the boundary value method is 11.33 dB. The previous point of view of worst case leads to an elevation angle of -1.87 degree and an attenuation of 170.77 dB. With this kind of attenuation, every system would be unusable! It was found also for this case that with the nominal elevation angle, the distance of the tangent point to ground is 5.84 km; that of the worst case is 2.69 km. The nominal distance from source to target is 6383.84 km; for the worst case, it is 990.36 km.
There are many numerical methods to solve boundary value problems. For the Eikonal equation, due the good behavior of the refraction index just a simple Shooting method
Shooting method
In numerical analysis, the shooting method is a method for solving a boundary value problem by reducing it to the solution of an initial value problem...
can be used.
Conclusions
Of the three methods, the linear and the ITU methods require some coding since they are not presented as differential equations. These methods do not benefit from the help of standard numerical packages; however, only high school mathematics are required to understand the methods. The more technical eikonal equation can be solved using standard differential equations solvers offered by a few numerical software packages mentioned in the Wikipedia List of numerical analysis software and it offers a higher precision order.The attenuation mechanism as described here is only one amongst many others others. The full problem is much more complex.