Shooting method
Encyclopedia
In numerical analysis
, the shooting method is a method for solving a boundary value problem
by reducing it to the solution of an initial value problem
. The following exposition may be clarified by this illustration of the shooting method.
For a boundary value problem of a second-order ordinary differential equation
, the method is stated as follows.
Let
be the boundary value problem.
Let y(t; a) denote the solution of the initial value problem
Define the function F(a) as the difference between y(t1; a) and the specified boundary value y1.
If the boundary value problem has a solution, then F has a root,
and that root is just the value of y' (t0) which yields a solution y(t) of the boundary value problem.
The usual methods for finding roots may be employed here,
such as the bisection method
or Newton's method
.
In this case, the solution to the boundary value problem is usually given by:
where
is the solution to the initial value problem:
and
is the solution to the initial value problem:
See the proof for the precise condition under which this result holds.
is given as follows by Stoer and Burlisch (Section 7.3.1).
The initial value problem
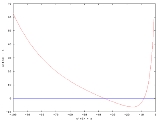
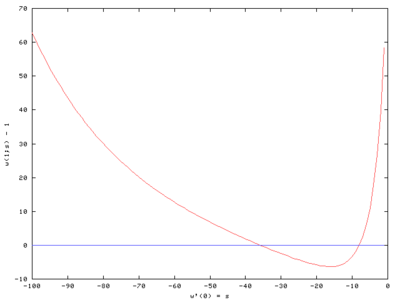
was solved for s = −1, −2, −3, ..., −100, and F(s) = w(1;s) − 1 plotted in the first figure.
Inspecting the plot of F,
we see that there are roots near −8 and −36.
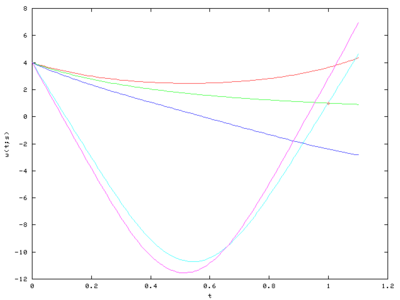
Some trajectories of w(t;s) are shown in the second figure.
Solutions of the initial value problem were computed by using the LSODE algorithm, as implemented in the mathematics package GNU Octave
.
Stoer and Bulirsch state that there are two solutions,
which can be found by algebraic methods.
These correspond to the initial conditions w′(0) = −8 and w′(0) = −35.9 (approximately).
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the shooting method is a method for solving a boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
by reducing it to the solution of an initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
. The following exposition may be clarified by this illustration of the shooting method.
For a boundary value problem of a second-order ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
, the method is stated as follows.
Let
be the boundary value problem.
Let y(t; a) denote the solution of the initial value problem
Define the function F(a) as the difference between y(t1; a) and the specified boundary value y1.
If the boundary value problem has a solution, then F has a root,
and that root is just the value of y
The usual methods for finding roots may be employed here,
such as the bisection method
Bisection method
The bisection method in mathematics is a root-finding method which repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing. It is a very simple and robust method, but it is also relatively slow...
or Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
.
Linear shooting method
The boundary value problem is linear if f has the formIn this case, the solution to the boundary value problem is usually given by:
where
is the solution to the initial value problem:and
is the solution to the initial value problem:See the proof for the precise condition under which this result holds.
Example
A boundary value problemBoundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
is given as follows by Stoer and Burlisch (Section 7.3.1).
The initial value problem
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
was solved for s = −1, −2, −3, ..., −100, and F(s) = w(1;s) − 1 plotted in the first figure.
Inspecting the plot of F,
we see that there are roots near −8 and −36.
Some trajectories of w(t;s) are shown in the second figure.
Solutions of the initial value problem were computed by using the LSODE algorithm, as implemented in the mathematics package GNU Octave
GNU Octave
GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB...
.
Stoer and Bulirsch state that there are two solutions,
which can be found by algebraic methods.
These correspond to the initial conditions w′(0) = −8 and w′(0) = −35.9 (approximately).
See also
- Direct multiple shooting methodDirect multiple shooting methodIn the area of mathematics known as numerical ordinary differential equations, the direct multiple shooting method is a numerical method for the solution of boundary value problems...
- Computation of radiowave attenuation in the atmosphereComputation of radiowave attenuation in the atmosphereOne of the causes of attenuation of radio propagation is the absorption by the atmosphere. There are many well known facts on the phenomenon and qualitative treatments in textbooks. A document published by the International Telecommunication Union...
External links
- Brief Description of ODEPACK (at NetlibNetlibNetlib is a repository of software for scientific computing maintained by AT&T, Bell Laboratories, the University of Tennessee and Oak Ridge National Laboratory. Netlib comprises a large number of separate programs and libraries...
; contains LSODE) - Shooting method of solving boundary value problems – Notes, PPT, Maple, Mathcad, Matlab, Mathematica at Holistic Numerical Methods Institute http://numericalmethods.eng.usf.edu
- Shooting Method for Boundary Value Problems
- Boundary value problems: the shooting method