In mathematics

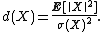
Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 — specifically, in probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

 — the concentration dimension of a Banach space

Banach space

In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

-valued random variable

Random variable

In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...

 is a numerical measure of how “spread out” the random variable is compared to the norm

Norm (mathematics)

In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...

 on the space.

Definition

Let (B, || ||) be a Banach space and let X be a Gaussian random variable taking values in B. That is, for every linear functional ℓ in the dual space

Dual space

In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...

 B^∗, the real-valued random variable ⟨ℓ, X⟩ has a normal distribution. Define


Then the concentration dimension d(X) of X is defined by

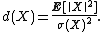
Examples

• If B is n-dimensional Euclidean space
  Euclidean space
  In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
  
   Rⁿ with its usual Euclidean norm, and X is a standard Gaussian random variable, then σ(X) = 1 and E[||X||²] = n, so d(X) = n.
• If B is Rⁿ with the supremum norm, then σ(X) = 1 but E[||X||²] (and hence d(X)) is of the order of log(n).