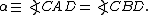
Concyclic points
Encyclopedia
In geometry
, a set of points
is said to be concyclic (or cocyclic) if they lie on a common circle
.
 A circle can be drawn around
A circle can be drawn around
any triangle
. A quadrilateral that can be inscribed inside a circle is said to be a cyclic quadrilateral
.
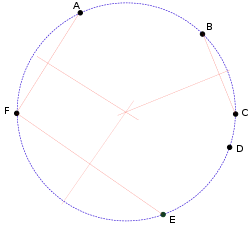
In general the centre O of a circle on which points P and Q lie must be such that OP and OQ are equal distances. Therefore O must lie on the perpendicular bisector of the line segment
PQ. For n distinct points there are n(n− 1)/2 such lines to draw, and the concyclic condition is that they all meet in a single point.
A quadrilateral
in which the four vertices are concyclic is called a cyclic quadrilateral
. More generally, a polygon in which all vertices are concyclic is called a cyclic polygon. Three noncollinear
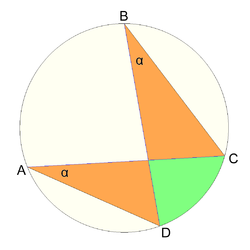
points A, B, and C are concyclic to a single circle. Four different points A, B, C, and D are cyclic if and only if
(see diagram):
This condition is equivalent to the condition that opposite angles in the quadrilateral be supplementary. Four points in the complex plane
are either concyclic or collinear if and only if their cross-ratio
is real
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a set of points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
is said to be concyclic (or cocyclic) if they lie on a common circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
.


Circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
any triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
. A quadrilateral that can be inscribed inside a circle is said to be a cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
.
In general the centre O of a circle on which points P and Q lie must be such that OP and OQ are equal distances. Therefore O must lie on the perpendicular bisector of the line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
PQ. For n distinct points there are n(n− 1)/2 such lines to draw, and the concyclic condition is that they all meet in a single point.
A quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
in which the four vertices are concyclic is called a cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
. More generally, a polygon in which all vertices are concyclic is called a cyclic polygon. Three noncollinear
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
points A, B, and C are concyclic to a single circle. Four different points A, B, C, and D are cyclic if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
(see diagram):
This condition is equivalent to the condition that opposite angles in the quadrilateral be supplementary. Four points in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
are either concyclic or collinear if and only if their cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
is real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
.
External links
- Four Concyclic Points by Michael Schreiber, The Wolfram Demonstrations Project.