
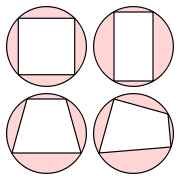
Cyclic quadrilateral
Encyclopedia
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, a cyclic quadrilateral is a quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
whose vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
all lie on a single circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. This circle is called the circumcircle or circumscribed circle
Circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed quadrilateral. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.
The word cyclic is from the Greek "kuklos" which means circle or wheel.
Special cases
Any squareSquare (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
, isosceles trapezoid
Isosceles trapezoid
In Euclidean geometry, an isosceles trapezoid is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides, making it automatically a trapezoid...
, or antiparallelogram
Antiparallelogram
An antiparallelogram is a quadrilateral in which, like a parallelogram, the pairs of nonadjacent sides are congruent, but in which two opposite sides intersect and are therefore not parallel.-Properties:Every antiparallelogram has an axis of symmetry through its crossing point...
is cyclic. A kite
Kite (geometry)
In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other...
is cyclic if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it has two right angles. A bicentric quadrilateral
Bicentric quadrilateral
In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. This means they have all the properties of both tangential quadrilaterals and cyclic quadrilaterals...
is a cyclic quadrilateral that is also tangential
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
and an ex-bicentric quadrilateral is a cyclic quadrilateral that is also ex-tangential
Ex-tangential quadrilateral
In Euclidean geometry, an ex-tangential quadrilateral is a convex quadrilateral where the extensions of all four sides are tangent to a circle outside the quadrilateral. It has also been called an exscriptible quadrilateral. The circle is called its excircle or its escribed circle, its radius the...
.
Characterizations
A convex quadrilateral is cyclic if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the four perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
bisectors to the sides are concurrent. This common point is the circumcenter.
A convex quadrilateral ABCD is cyclic if and only if its opposite angles are supplementary, that is
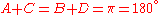 . Equivalently, a convex quadrilateral is cyclic if and only if each exterior angle is equal to the opposite interior angle.
. Equivalently, a convex quadrilateral is cyclic if and only if each exterior angle is equal to the opposite interior angle.Another necessary and sufficient condition for a convex quadrilateral ABCD to be cyclic is that an angle between a side and a diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
is equal to the angle between the opposite side and the other diagonal. That is, for example,

Yet another characterization is that a convex quadrilateral ABCD is cyclic if and only if
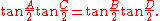
Area
The areaArea
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
K of a cyclic quadrilateral with sides a, b, c, d is given by Brahmagupta's formula
Brahmagupta's formula
In Euclidean geometry, Brahmagupta's formula finds the area of any quadrilateral given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle.- Basic form :...
where s, the semiperimeter
Semiperimeter
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name...
, is
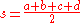 . It is a corollary
. It is a corollaryCorollary
A corollary is a statement that follows readily from a previous statement.In mathematics a corollary typically follows a theorem. The use of the term corollary, rather than proposition or theorem, is intrinsically subjective...
to Bretschneider's formula since opposite angles are supplementary. If also
 , the cyclic quadrilateral becomes a triangle and the formula is reduced to Heron's formula.
, the cyclic quadrilateral becomes a triangle and the formula is reduced to Heron's formula.The cyclic quadrilateral has maximal
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
area among all quadrilaterals having the same sequence of side lengths. This is another corollary to Bretschneider's formula. It can also be proved using calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
.
Four unequal lengths, each less than then sum of the other three, are the sides of each of three non-congruent cyclic quadrilaterals, which by Brahmagupta's formula all have the same area. Specifically, for sides a, b, c, and d, side a could be opposite any of side b, side c, or side d.
The area of a cyclic quadrilateral with successive sides a, b, c, d and angle B between sides a and b can be expressed as

or
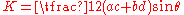
where
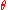 is the angle between the diagonals. If A is an oblique angle
is the angle between the diagonals. If A is an oblique angleOblique Angle
Oblique angle can refer to:*An angle which is not a multiple of 90°*Another word for "Dutch angle" in cinematography...
, the area can also be expressed as
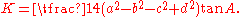
Another formula is

where R is the radius in the circumcircle
Circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
.
In terms of the sides a, b, c, d, the area satisfies the inequality

Diagonals
Ptolemy's theoremPtolemy's theorem
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral . The theorem is named after the Greek astronomer and mathematician Ptolemy...
expresses the product of the lengths of the two diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
s p and q of a cyclic quadrilateral as equal to the sum of the products ac and bd of opposite sides:
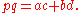
The converse is also true. That is, if this equation is satisfied in a convex quadrilateral, then it is a cyclic quadrilateral. Thus Ptolemy's theorem is another characterization of cyclic quadrilaterals.
In any convex quadrilateral, the two diagonals together partition the quadrilateral into four triangles; in a cyclic quadrilateral, opposite pairs of these four triangles are similar
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
to each other.
Ptolemy's second theorem states that a cyclic quadrilateral with successive vertices A, B, C, D and sides a = AB, b = BC, c = CD, and d = DA, and with diagonals p = AC and q = BD, has
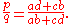
The lengths of the diagonals are given in terms of the sides (using the same notations as above) as
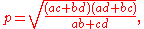
and
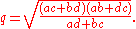
For the sum of the diagonals we have the inequality
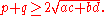
Equality holds if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the diagonals have equal length, which can be proved using the AM-GM inequality.
If the intersection of the diagonals divides one diagonal into segments of lengths e and f, and divides the other diagonal into segments of lengths g and h, then
 . This is known as the intersecting chords theorem.
. This is known as the intersecting chords theorem.Angle formulas
For a cyclic quadrilateral with successive sides a, b, c, d, semiperimeterSemiperimeter
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name...
s, and angle A between sides a and d, the trigonometric functions of A are given by

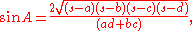
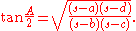
The angle
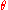 between the diagonals satisfies
between the diagonals satisfies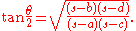
If the extensions of opposite sides a and c intersect at an angle
 , then
, then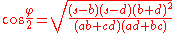
where s is the semiperimeter
Semiperimeter
In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name...
.
Parameshvara's formula
A cyclic quadrilateral with successive sides a, b, c, d and semiperimeter s has circumradius (the radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the circumcircle
Circumscribed circle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle which passes through all the vertices of the polygon. The center of this circle is called the circumcenter....
) given by
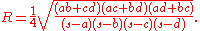
It was derived by the Indian mathematician Vatasseri Parameshvara
Parameshvara
Vatasseri Parameshvara Nambudiri was a major Indian mathematician and astronomer of the Kerala school of astronomy and mathematics founded by Madhava of Sangamagrama. He was also an astrologer...
in the fifteenth century.
Other properties
- There are no cyclic quadrilaterals with rational area and with unequal rational sides in either arithmeticArithmetic progressionIn mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
or geometric progressionGeometric progressionIn mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
.
- Four line segments, each perpendicularPerpendicularIn geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to one side of a cyclic quadrilateral and passing through the opposite side's midpointMidpointThe midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...
, are concurrentConcurrent linesIn geometry, two or more lines are said to be concurrent if they intersect at a single point.In a triangle, four basic types of sets of concurrent lines are altitudes, angle bisectors, medians, and perpendicular bisectors:...
. These line segments are called the maltitudes, which is an abbreviation for midpoint altitude.
- If the opposite sides of a cyclic quadrilateral are extended to meet at E and F, then the internal angle bisectors of the angles at E and F are perpendicular. If M and N are the midpoints of the diagonals AC and BD, then
- In a cyclic quadrilateral ABCD, the incenterIncircle and excircles of a triangleIn geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides...
s in triangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s ABC, BCD, CDA, and DAB are the vertices of a rectangleRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
, see Japanese theorem for cyclic quadrilaterals.
Properties of cyclic quadrilaterals that are also orthodiagonal
- Brahmagupta's theorem states that for a cyclic quadrilateral that is also orthodiagonalOrthodiagonal quadrilateralIn Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal to each other....
(has mutually perpendicular diagonals), the perpendicular from any side through the point of intersection of the diagonals bisects the other side.
- If a cyclic quadrilateral is also orthodiagonal, the distance from the circumcenter (the center of the circumscribed circle) to any side equals half the length of the opposite side.
- For a cyclic orthodiagonal quadrilateral, suppose the intersection of the diagonals divides one diagonal into segments of lengths p1 and p2 and divides the other diagonal into segments of lengths q1 and q2. Then
- where D is the diameterDiameterIn geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of the circumcircle. This holds because the diagonals are perpendicular chords of a circle. Equivalently, letting R = D / 2 be the radiusRadiusIn classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the circumcircle, the average of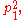
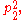
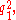 and
and 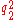 is
is  . Moreover, the equations a2 + c2 = b2 + d2 = D2 imply that in an orthodiagonal cyclic quadrilateral, the sum of the squares of the sides equals eight times the square of the circumradius.
. Moreover, the equations a2 + c2 = b2 + d2 = D2 imply that in an orthodiagonal cyclic quadrilateral, the sum of the squares of the sides equals eight times the square of the circumradius.
- If an orthodiagonal quadrilateral is also cyclic, then the midpoints of the sides and the feet of the perpendiculars from these midpoints to the opposite sides lie on a circle centered at the centroid of the quadrilateral. This circle is called the eight point circle.
See also
- Bicentric quadrilateralBicentric quadrilateralIn Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. This means they have all the properties of both tangential quadrilaterals and cyclic quadrilaterals...
- Brahmagupta's theorem on perpendicular diagonals of cyclic quadrilaterals
- Ex-tangential quadrilateralEx-tangential quadrilateralIn Euclidean geometry, an ex-tangential quadrilateral is a convex quadrilateral where the extensions of all four sides are tangent to a circle outside the quadrilateral. It has also been called an exscriptible quadrilateral. The circle is called its excircle or its escribed circle, its radius the...
- Cyclic polygon
- Japanese theorem for cyclic quadrilaterals
- Orthodiagonal quadrilateralOrthodiagonal quadrilateralIn Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal to each other....
- Ptolemy's table of chordsPtolemy's table of chordsThe table of chords, created by the astronomer and geometer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function...
- Ptolemy's theoremPtolemy's theoremIn Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral . The theorem is named after the Greek astronomer and mathematician Ptolemy...
- Tangential quadrilateralTangential quadrilateralIn Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
, a quadrilateral all of whose sides are tangent to a single circle
External links
- Derivation of Formula for the Area of Cyclic Quadrilateral
- Incenters in Cyclic Quadrilateral at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Four Concurrent Lines in a Cyclic Quadrilateral at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...




