Orthodiagonal quadrilateral
Encyclopedia
In Euclidean geometry
, an orthodiagonal quadrilateral is a quadrilateral
in which the diagonal
s cross at right angle
s. In other words, it is a four-sided figure in which the line segment
s between non-adjacent vertices
are orthogonal to each other.
is an orthodiagonal quadrilateral in which one diagonal is a line of symmetry. The kites are exactly the orthodiagonal quadrilaterals that contain a circle
tangent to all four of their sides; that is, the kites are the tangential
orthodiagonal quadrilaterals.
A rhombus
is an orthodiagonal quadrilateral with two pairs of parallel sides (that is, an orthodiagonal quadrilateral that is also a parallelogram
).
A square
is a limiting case of both a kite and a rhombus.
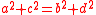
This follows from the Pythagorean theorem
, by which either of these two sums of two squares can be expanded to equal the sum of the four squared distances from the quadrilateral's vertices to the point where the diagonals cross. Conversely, any quadrilateral in which must be orthodiagonal.
The orthodiagonal quadrilateral has the biggest area of all convex quadrilaterals with given diagonals.
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, an orthodiagonal quadrilateral is a quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
in which the diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
s cross at right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
s. In other words, it is a four-sided figure in which the line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
s between non-adjacent vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
are orthogonal to each other.
Special cases
A kiteKite (geometry)
In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other...
is an orthodiagonal quadrilateral in which one diagonal is a line of symmetry. The kites are exactly the orthodiagonal quadrilaterals that contain a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
tangent to all four of their sides; that is, the kites are the tangential
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
orthodiagonal quadrilaterals.
A rhombus
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
is an orthodiagonal quadrilateral with two pairs of parallel sides (that is, an orthodiagonal quadrilateral that is also a parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
).
A square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
is a limiting case of both a kite and a rhombus.
Characterization
For any orthodiagonal quadrilateral, the sum of the squares of two opposite sides equals that of the other two opposite sides: for successive sides , , , and , we have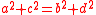This follows from the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, by which either of these two sums of two squares can be expanded to equal the sum of the four squared distances from the quadrilateral's vertices to the point where the diagonals cross. Conversely, any quadrilateral in which must be orthodiagonal.
Area
The area K of an orthodiagonal quadrilateral equals one half the product of the lengths of the diagonals p, q:The orthodiagonal quadrilateral has the biggest area of all convex quadrilaterals with given diagonals.
Other properties
- Orthodiagonal quadrilaterals are the only quadrilaterals for which the sides and the angle formed by the diagonals do not uniquely determine the area. For example, two rhombi both having common side a (and of course both having a right angle between the diagonals), but one having a smaller acute angle than the other, have different areas (the area of the former approaching zero as the acute angle approaches zero).
- In an orthodiagonal quadrilateral the two lines joining the midpoints of the pairs of opposite sides are of equal length.
- If squareSquare (geometry)In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
s are erected outward on the sides of a convex quadrilateralQuadrilateralIn Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
, then their centreCentre (geometry)In geometry, the centre of an object is a point in some sense in the middle of the object. If geometry is regarded as the study of isometry groups then the centre is a fixed point of the isometries.-Circles:...
s (centroidCentroidIn geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
s) are the vertices of an orthodiagonal quadrilateral with diagonals of equal length.
- The quadrilateral formed by the midpoints of the sides of an orthodiagonal quadrilateral is a rectangleRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
.
Properties of orthodiagonal quadrilaterals that are also cyclic
- For a cyclicCyclic quadrilateralIn Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
orthodiagonal quadrilateral (one that can be inscribed in a circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
), suppose the intersection of the diagonals divides one diagonal into segments of lengths p1 and p2 and divides the other diagonal into segments of lengths q1 and q2. Then
- where D is the diameterDiameterIn geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of the circumcircle. This holds because the diagonals are perpendicular chords of a circle. Equivalently, letting R = D / 2 be the radiusRadiusIn classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the circumcircle, the average of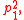
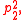
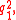and 
is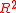 
. Moreover, the equations a2 + c2 = b2 + d2 = D2 imply that in an orthodiagonal cyclic quadrilateral, the sum of the squares of the sides equals eight times the square of the circumradius.
- Brahmagupta's theorem states that for a cyclic orthodiagonal quadrilateral, the perpendicular from any side through the point of intersection of the diagonals bisects the other side.
- If an orthodiagonal quadrilateral is also cyclic, the distance from the circumcenter (the center of the circumscribed circle) to any side equals half the length of the opposite side.
- If an orthodiagonal quadrilateral is also cyclic, then the midpoints of the sides and the feet of the perpendiculars from these midpoints to the opposite sides lie on a circle centered at the centroidCentroidIn geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
of the quadrilateral. This circle is called the eight point circle.
See also
- Bicentric quadrilateralBicentric quadrilateralIn Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. This means they have all the properties of both tangential quadrilaterals and cyclic quadrilaterals...
- Brahmagupta's theorem
- Cyclic quadrilateralCyclic quadrilateralIn Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
- Ex-tangential quadrilateralEx-tangential quadrilateralIn Euclidean geometry, an ex-tangential quadrilateral is a convex quadrilateral where the extensions of all four sides are tangent to a circle outside the quadrilateral. It has also been called an exscriptible quadrilateral. The circle is called its excircle or its escribed circle, its radius the...
- KiteKite (geometry)In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other...
- RhombusRhombusIn Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
- Tangential quadrilateralTangential quadrilateralIn Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...