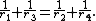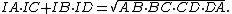Tangential quadrilateral - AbsoluteAstronomy.com

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

, a tangential quadrilateral or circumscribed quadrilateral is a convex

Convex polygon

In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...

quadrilateral

Quadrilateral

In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...

whose sides all lie tangent to a single circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

inscribed within the quadrilateral. This circle is called the incircle. Because tangential quadrilaterals can be drawn surrounding or circumscribing their incircles, they are also sometimes called circumscribable quadrilaterals. Another name for the same class of quadrilaterals is inscriptable quadrilaterals.

Special cases

Examples of tangential quadrilaterals are squares

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

, rhombi

Rhombus

In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...

, and kites

Kite (geometry)

In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other...

. The kites are exactly the tangential quadrilaterals that are also orthodiagonal

Orthodiagonal quadrilateral

In Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal to each other....

.
If a quadrilateral is both tangential and cyclic

Cyclic quadrilateral

In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...

, it is called a bicentric quadrilateral

Bicentric quadrilateral

In Euclidean geometry, a bicentric quadrilateral is a convex quadrilateral that has both an incircle and a circumcircle. This means they have all the properties of both tangential quadrilaterals and cyclic quadrilaterals...

Characterizations

In a tangential quadrilateral, the four angle bisectors meet at the center of the inscribed circle, and conversely a convex quadrilateral in which the four angle bisectors meet at a point must be tangential.

In a tangential quadrilateral, according to the Pitot theorem

Pitot theorem

In geometry, the Pitot theorem, named after the French engineer Henri Pitot, states that in a tangential quadrilateral the two sums of lengths of opposite sides are the same. The theorem is a consequence of the fact that two tangent line segments from a point outside the circle to the circle have...

, the two pairs of opposite sides add to the same total length, which equals the semiperimeter

Semiperimeter

In geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name...

of the quadrilateral:

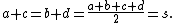
Conversely a convex quadrilateral in which a + c = b + d must be tangential.

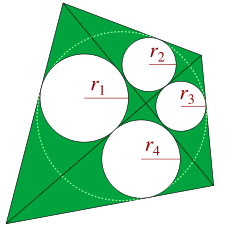
Chao and Simeonov observed another characterization of tangential quadrilaterals. The two diagonals of any convex quadrilateral partition the quadrilateral into four triangles. Let r₁, r₂, r₃, and r₄ denote the radii of the circles inscribed in the four successively adjacent triangles; then the quadrilateral is tangential if and only if

If opposite sides in a convex quadrilateral ABCD intersect at E and F, then it is tangential if and only if

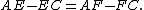
This characterization is almost the same as one of the equalities in Urquhart’s Theorem. The only differences are the signs on both sides; in Urquhart’s Theorem there are sums instead of differences.

Area

The area K of a tangential quadrilateral is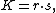

where s is the semiperimeter described above and r is the circle's radius (called the inradius).

A trigonometric formula for the area is

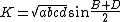
where B and D are opposite angles. For given side lengths, the area is maximum

Maxima and minima

In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...

when the quadrilateral is also cyclic

Cyclic quadrilateral

and hence a bicentric quadrilateral

Bicentric quadrilateral

. Then

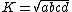since opposite angles are supplementary angles

Supplementary angles

Supplementary angles are pairs of angles that add up to 180 degrees. Thus the supplement of an angle of x degrees is an angle of degrees....

.

In fact, the area can be expressed in terms of only two sides and two opposite angles as

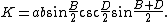
Another area formula is

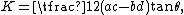
where 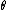is the angle between the diagonals, and still another is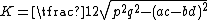

which gives the area in terms of the diagonals p, q and the sides a, b, c, d of the quadrilateral.

The area K can also be expressed in terms of the four tangent lengths. (The tangent length from any vertex is the distance from that vertex to either of the points where the incircle is tangent to the sides emanating from that vertex). If these are e, f, g, h, then the tangential quadrilateral has the area

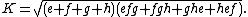
Inradius

The inradius in a tangential quadrilateral with consecutive sides a, b, c, d is given by

where K is the area of the quadrilateral. For a tangential quadrilateral with given sides, the inradius is maximum

Maxima and minima

when the quadrilateral is also cyclic

Cyclic quadrilateral

(and hence a bicentric quadrilateral

Bicentric quadrilateral

).

In terms of the tangent lengths, the incircle has radius

Diagonals and tangency chords

The lengths of the diagonals p and q are in terms of the tangent lengths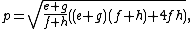

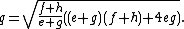
The two line segmets that connect the points of tangency of the incircle at opposite sides of the tangential quadrilateral are called the tangency chords. The lengths k and l of these are

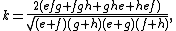
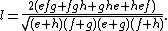
Other properties

The line segments between the center of the inscribed circle and the points where it is tangent to the quadrilateral partition the quadrilateral into kites
Kite (geometry)
In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other...

.

The two diagonals and the two tangency chords are concurrent. One way to see this is as a limiting case of Brianchon's theorem
Brianchon's theorem
In geometry, Brianchon's theorem, named after Charles Julien Brianchon , is as follows. Let ABCDEF be a hexagon formed by six tangent lines of a conic section...

, which states that a hexagon all of whose sides are tangent to a single conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...

has three diagonals that meet at a point. From a tangential quadrilateral, one can form a hexagon with two 180° angles, by placing two new vertices at two opposite points of tangency; all six of the sides of this hexagon lie on lines tangent to the inscribed circle, so its diagonals meet at a point. But two of these diagonals are the same as the diagonals of the tangential quadrilateral, and the third diagonal of the hexagon is the line through two opposite points of tangency. Repeating this same argument with the other two points of tangency completes the proof of the result.

If a four-bar linkage is made in the form of a tangential quadrilateral, then it will remain tangential no matter how the linkage is flexed, provided the quadrilateral remains convex.

In a tangential quadrilateral ABCD, the incircles in triangles ABC and ADC are tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

to each other.

If a line cuts a tangential quadrilateral into two polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

s with equal areas and equal perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...

s, then that line passes through the incenter.

If M and N are the midpoints of the diagonals in a tangential quadrilateral with incenter I, then the points M, I, and N are collinear.

If the incircle is tangent to the sides AB, BC, CD, DA at X, Y, Z, W respectively, then the lines XY, WZ and AC are concurrent.

If I is the center of the incircle in tangential quadrilateral ABCD, then

The center I of the incircle in tangential quadrilateral ABCD coincides with the centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...

of the quadrilateral if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

Conditions for a tangential quadrilateral to be another type of quadrilateral

A tangential quadrilateral is a rhombus
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...

if and only if its opposite angles are equal.

If the inscribed circle is tangent to the quadrilateral at points T, U, V, W in sequence, then the tangential quadrilateral is also cyclic

Cyclic quadrilateral

(and hence bicentric

Bicentric quadrilateral

) if and only if TV is perpendicular to UW.

A tangential quadrilateral is a kite
Kite
A kite is a tethered aircraft. The necessary lift that makes the kite wing fly is generated when air flows over and under the kite's wing, producing low pressure above the wing and high pressure below it. This deflection also generates horizontal drag along the direction of the wind...

if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

any one of the following conditions is true:

The area is one half the product of the diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...

s
The diagonals are perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
The two line segments connecting opposite points of tangency have equal length
One pair of opposite tangent lengths have equal length
The bimedians have equal length
The products of opposite sides are equal
The center of the incircle lies on the longest diagonal

Special cases

Characterizations

Area

Inradius

Diagonals and tangency chords

Other properties

Conditions for a tangential quadrilateral to be another type of quadrilateral

See also