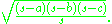Semiperimeter
Encyclopedia
In geometry
, the semiperimeter of a polygon is half its perimeter
. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name. When the semiperimeter occurs as part of a formula, it is typically denoted by the letter s.
The semiperimeter is used most often for triangles; the formula for the semiperimeter of a triangle with side lengths a, b, and c is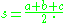
The area of any triangle is the product of its inradius and its semiperimeter; the same area formula also applies to tangential quadrilateral
s, in which pairs of opposite sides have lengths adding to the semiperimeter. The area of a triangle can also be calculated from its semiperimeter and side lengths using Heron's formula:
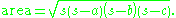
The simplest form of Brahmagupta's formula
, for the area of a cyclic quadrilateral
, has a similar form:
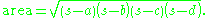
The circumradius R of a triangle can also be calculated from the semiperimeter and side lengths: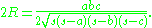
This formula can be derived from the law of sines
.
The radius of the incircle (also known as the inradius) is
In any triangle, the points where the excircles touch the triangle and the opposite vertices of the triangle partition the triangle's perimeter into two equal lengths. That is, if A, B, C, A', B', and C' are as shown in the figure, then
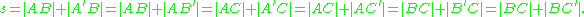
If one connects each such point of tangency with its opposite vertex by a line (shown red in the figure), these three lines meet in the Nagel point
of the triangle.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the semiperimeter of a polygon is half its perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name. When the semiperimeter occurs as part of a formula, it is typically denoted by the letter s.
The semiperimeter is used most often for triangles; the formula for the semiperimeter of a triangle with side lengths a, b, and c is
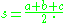
The area of any triangle is the product of its inradius and its semiperimeter; the same area formula also applies to tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
s, in which pairs of opposite sides have lengths adding to the semiperimeter. The area of a triangle can also be calculated from its semiperimeter and side lengths using Heron's formula:
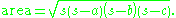
The simplest form of Brahmagupta's formula
Brahmagupta's formula
In Euclidean geometry, Brahmagupta's formula finds the area of any quadrilateral given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle.- Basic form :...
, for the area of a cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
, has a similar form:
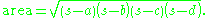
The circumradius R of a triangle can also be calculated from the semiperimeter and side lengths:
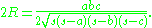
This formula can be derived from the law of sines
Law of sines
In trigonometry, the law of sines is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles...
.
The radius of the incircle (also known as the inradius) is
In any triangle, the points where the excircles touch the triangle and the opposite vertices of the triangle partition the triangle's perimeter into two equal lengths. That is, if A, B, C, A', B', and C' are as shown in the figure, then
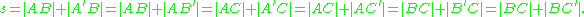
If one connects each such point of tangency with its opposite vertex by a line (shown red in the figure), these three lines meet in the Nagel point
Nagel point
In geometry, the Nagel point is a point associated with any triangle. Given a triangle ABC, let TA, TB, and TC be the extouch points in which the A-excircle meets line BC, the B-excircle meets line CA, and C-excircle meets line AB, respectively...
of the triangle.