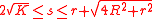Bicentric quadrilateral
Encyclopedia
In Euclidean geometry
, a bicentric quadrilateral is a convex
quadrilateral
that has both an incircle and a circumcircle. This means they have all the properties of both tangential quadrilateral
s and cyclic quadrilateral
s. Another name is chord-tangent quadrilateral.
and right kites, that is, kites
with two opposite right angles
.
opposite sides satisfy Pitot's theorem and opposite angles are supplementary, that is
and 
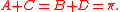
Three other characterizations concern the points where the incircle in a tangential quadrilateral
is tangent to the sides. If the incircle is tangent to the sides AB, BC, CD, DA at W, X, Y, Z respectively, then a tangential quadrilateral ABCD is also cyclic if and only if any of
If E, F, G, H are the midpoints of WX, XY , YZ, ZW respectively, then the tangential quadrilateral
ABCD is also cyclic if and only if
the quadrilateral
EFGH is a rectangle
.
According to another characterization, if I is the incenter in a tangential quadrilateral
where the extensions of opposite sides intersect at J and K, then the quadrilateral
is also cyclic if and only if JIK is a right angle
.
Yet another is that a tangential quadrilateral
ABCD is cyclic if and only if its Newton line is perpendicular
to the Newton line of its contact quadrilateral WXYZ. (The Newton line of a quadrilateral is the line defined by the midpoints of its diagonals.)
K of a bicentric quadrilateral with sides a, b, c, d is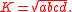
This is a special case of Brahmagupta's formula
. It can also be derived directly from the trigonometric formula for the area of a tangential quadrilateral.
If a bicentric quadrilateral has tangency chords k, l and diagonals p, q, then it has the area
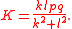
Another formula for the area is
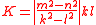
where m and n are the bimedians of the quadrilateral.
The area can also be expressed in terms of the tangent lengths e, f, g, h as
Yet another formula for the area of bicentric quadrilateral ABCD is
where I is the center of the incircle. In terms of two adjacent angles and the radius r of the incircle, the area is given as
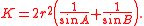
If r and R are the inradius and the circumradius respectively, then the area
K satisfies the inequalities
There is equality (on either side) only if the quadrilateral is a square
.
Another inequality for the area is
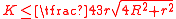
where r and R are the inradius and the circumradius respectively.
The angle
between the diagonals can be calculated from
The inradius can also be expressed in terms of the consecutive tangent lengths e, f, g, h according to
These two formulas are in fact necessary and sufficient conditions for a tangential quadrilateral
with inradius r to be cyclic
.
The circumradius R is given as a special case of Parameshvara
's formula. It is
The two radii satisfy the inequality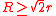
. It holds with equality only when the two circles are concentric
(have the same center as each other); then the quadrilateral is a square
. This inequality follows from the double inequality for the area.
Another inequality concerning the two radii in a bicentric quadrilateral ABCD is
where I is the incenter.
In a bicentric quadrilateral with diagonals
p and q, it holds that
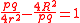
where r and R are the inradius and the circumradius respectively.
or equivalently
.
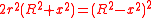It was derived by Nicolaus Fuss (1755–1826) in 1792. Solving for x yields
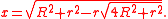
Fuss's theorem says that if a quadrilateral is bicentric, then its two associated circles are related according to the above equations. In fact the converse also holds: given two circles (one within the other) with radii R and r and distance x between their centers satisfying the condition in Fuss' theorem, there exists a convex quadrilateral inscribed in one of them and tangent to the other.
Applying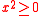
to the expression of Fuss's theorem for x in terms of r and R is another way to obtain the above-mentioned inequality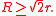 
Another formula for the distance x between the centers of the incircle and the circumcircle is due to the American mathematician Leonard Carlitz
(1907–1999). It states that
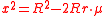
where r and R are the inradius and the circumradius respectively, and
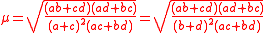
where a, b, c, d are the sides of the bicentric quadrilateral. Carlitz' identity is a generalization of Euler's theorem in geometry
to a bicentric quadrilateral.
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, a bicentric quadrilateral is a convex
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
that has both an incircle and a circumcircle. This means they have all the properties of both tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
s and cyclic quadrilateral
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
s. Another name is chord-tangent quadrilateral.
Special cases
Examples of bicentric quadrilaterals are squaresSquare (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
and right kites, that is, kites
Kite (geometry)
In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other...
with two opposite right angles
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
.
Characterizations
A convex quadrilateral ABCD with sides a, b, c, d is bicentric if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
opposite sides satisfy Pitot's theorem and opposite angles are supplementary, that is
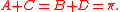
and Three other characterizations concern the points where the incircle in a tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
is tangent to the sides. If the incircle is tangent to the sides AB, BC, CD, DA at W, X, Y, Z respectively, then a tangential quadrilateral ABCD is also cyclic if and only if any of
(That is, the contact quadrilateral WXYZ is an orthodiagonal quadrilateralOrthodiagonal quadrilateralIn Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal to each other....
.)
If E, F, G, H are the midpoints of WX, XY , YZ, ZW respectively, then the tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
ABCD is also cyclic if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
EFGH is a rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
.
According to another characterization, if I is the incenter in a tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
where the extensions of opposite sides intersect at J and K, then the quadrilateral
Quadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
is also cyclic if and only if JIK is a right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
.
Yet another is that a tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
ABCD is cyclic if and only if its Newton line is perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the Newton line of its contact quadrilateral WXYZ. (The Newton line of a quadrilateral is the line defined by the midpoints of its diagonals.)
Area
The areaArea
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
K of a bicentric quadrilateral with sides a, b, c, d is
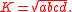
This is a special case of Brahmagupta's formula
Brahmagupta's formula
In Euclidean geometry, Brahmagupta's formula finds the area of any quadrilateral given the lengths of the sides and some of the angles. In its most common form, it yields the area of quadrilaterals that can be inscribed in a circle.- Basic form :...
. It can also be derived directly from the trigonometric formula for the area of a tangential quadrilateral.
If a bicentric quadrilateral has tangency chords k, l and diagonals p, q, then it has the area
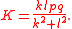
Another formula for the area is
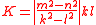
where m and n are the bimedians of the quadrilateral.
The area can also be expressed in terms of the tangent lengths e, f, g, h as
Yet another formula for the area of bicentric quadrilateral ABCD is
where I is the center of the incircle. In terms of two adjacent angles and the radius r of the incircle, the area is given as
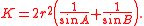
If r and R are the inradius and the circumradius respectively, then the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
K satisfies the inequalities
There is equality (on either side) only if the quadrilateral is a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
.
Another inequality for the area is
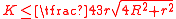
where r and R are the inradius and the circumradius respectively.
Angle formulas
If a, b, c, d are the length of the sides AB, BC, CD, DA respectively in a bicentric quadrilateral ABCD, then its vertex angles are given byThe angle
between the diagonals can be calculated fromInradius and circumradius
The inradius r of a bicentric quadrilateral is determined by the sides a, b, c, d according toThe inradius can also be expressed in terms of the consecutive tangent lengths e, f, g, h according to
These two formulas are in fact necessary and sufficient conditions for a tangential quadrilateral
Tangential quadrilateral
In Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...
with inradius r to be cyclic
Cyclic quadrilateral
In Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
.
The circumradius R is given as a special case of Parameshvara
Parameshvara
Vatasseri Parameshvara Nambudiri was a major Indian mathematician and astronomer of the Kerala school of astronomy and mathematics founded by Madhava of Sangamagrama. He was also an astrologer...
's formula. It is
The two radii satisfy the inequality
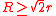. It holds with equality only when the two circles are concentricConcentric
Concentric objects share the same center, axis or origin with one inside the other. Circles, tubes, cylindrical shafts, disks, and spheres may be concentric to one another...
(have the same center as each other); then the quadrilateral is a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
. This inequality follows from the double inequality for the area.
Another inequality concerning the two radii in a bicentric quadrilateral ABCD is
where I is the incenter.
In a bicentric quadrilateral with diagonals
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
p and q, it holds that
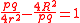
where r and R are the inradius and the circumradius respectively.
Fuss' theorem and Carlitz' identity
Fuss' theorem gives a relation between the inradius r, the circumradius R and the distance x between the incenter I and the circumcenter O, for any bicentric quadrilateral. The relation isor equivalently
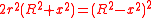.It was derived by Nicolaus Fuss (1755–1826) in 1792. Solving for x yields
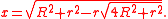
Fuss's theorem says that if a quadrilateral is bicentric, then its two associated circles are related according to the above equations. In fact the converse also holds: given two circles (one within the other) with radii R and r and distance x between their centers satisfying the condition in Fuss' theorem, there exists a convex quadrilateral inscribed in one of them and tangent to the other.
Applying
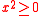to the expression of Fuss's theorem for x in terms of r and R is another way to obtain the above-mentioned inequality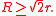 Another formula for the distance x between the centers of the incircle and the circumcircle is due to the American mathematician Leonard Carlitz
Leonard Carlitz
Leonard Carlitz was an American mathematician. Carlitz supervised 44 Doctorates at Duke University and published over 770 papers.- Chronology :* 1907 Born Philadelphia, PA, USA* 1927 BA, University of Pennsylvania...
(1907–1999). It states that
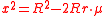
where r and R are the inradius and the circumradius respectively, and
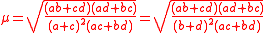
where a, b, c, d are the sides of the bicentric quadrilateral. Carlitz' identity is a generalization of Euler's theorem in geometry
Euler's theorem in geometry
In geometry, Euler's theorem, named after Leonhard Euler, states that the distance d between the circumcentre and incentre of a triangle can be expressed as d^2=R \,...
to a bicentric quadrilateral.
Other properties
- The circumcenter, the incenter, and the intersection of the diagonalsDiagonalA diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
in a bicentric quadrilateral are collinearCollinearityA set of points is collinear if they lie on a single line. Related concepts include:In mathematics:...
.
- An inequality for the product of the diagonals p, q in a bicentric quadrilateral is
-
- where a, b, c, d are the sides. This was proved by Murray Klamkin in 1967.
- If two circles, one within the other, are the incircle and the circumcircle of a bicentric quadrilateral, then every point on the circumcircle is the vertex of a bicentric quadrilateral having the same incircle and circumcircle. This was proved by the French mathematician Jean-Victor PonceletJean-Victor PonceletJean-Victor Poncelet was a French engineer and mathematician who served most notably as the commandant general of the École Polytechnique...
(1788–1867).
- The semiperimeterSemiperimeterIn geometry, the semiperimeter of a polygon is half its perimeter. Although it has such a simple derivation from the perimeter, the semiperimeter appears frequently enough in formulas for triangles and other figures that it is given a separate name...
s satisfies
- where K is the area of the bicentric quadrilateral and r, R are the inradius and circumradius respectively.
See also
- Bicentric polygonBicentric polygonIn geometry, a bicentric polygon is a tangential polygon which is also cyclic — that is, inscribed in an outer circle that passes through each vertex of the polygon. All triangles and all regular polygons are bicentric...
- Cyclic quadrilateralCyclic quadrilateralIn Euclidean geometry, a cyclic quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. Other names for these quadrilaterals are chordal quadrilateral and inscribed...
- Ex-tangential quadrilateralEx-tangential quadrilateralIn Euclidean geometry, an ex-tangential quadrilateral is a convex quadrilateral where the extensions of all four sides are tangent to a circle outside the quadrilateral. It has also been called an exscriptible quadrilateral. The circle is called its excircle or its escribed circle, its radius the...
- Orthodiagonal quadrilateralOrthodiagonal quadrilateralIn Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal to each other....
- Tangential quadrilateralTangential quadrilateralIn Euclidean geometry, a tangential quadrilateral or circumscribed quadrilateral is a convex quadrilateral whose sides all lie tangent to a single circle inscribed within the quadrilateral. This circle is called the incircle...