Bicentric polygon
Encyclopedia
In geometry, a bicentric polygon is a tangential polygon
(a polygon all of whose sides are tangent to an inner incircle) which is also cyclic — that is, inscribe
d in an outer circle that passes through each vertex of the polygon. All triangle
s and all regular polygon
s are bicentric. On the other hand, a rectangle
with unequal sides is not bicentric, because no circle can be tangent to all four sides.
and circumcircle respectively are related by the equation
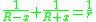
where x is the distance between the centers of the circles. This is one version of Euler's triangle formula.
s are bicentric (having both an incircle and a circumcircle). Given two circles (one within the other) with radii R and r where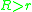
, there exists a convex quadrilateral inscribed in one of them and tangent to the other if and only if
their radii satisfy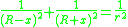
where x is the distance between their centers. This condition is known as Fuss' theorem.
For some regular polygons which can be constructed with compass and ruler, we have the following formulas for the relation between the common edge
length a, the radius r of the incircle
, and the radius R of the circumcircle:
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
(a polygon all of whose sides are tangent to an inner incircle) which is also cyclic — that is, inscribe
Inscribe
right|thumb|An inscribed triangle of a circleIn geometry, an inscribed planar shape or solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "Figure F is inscribed in figure G" means precisely the same thing as "figure G is circumscribed about...
d in an outer circle that passes through each vertex of the polygon. All triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s and all regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s are bicentric. On the other hand, a rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
with unequal sides is not bicentric, because no circle can be tangent to all four sides.
Triangles
In a triangle, the radii r and R of the incircleIncircle and excircles of a triangle
In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides...
and circumcircle respectively are related by the equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
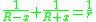
where x is the distance between the centers of the circles. This is one version of Euler's triangle formula.
Bicentric quadrilaterals
Not all quadrilateralQuadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
s are bicentric (having both an incircle and a circumcircle). Given two circles (one within the other) with radii R and r where
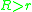, there exists a convex quadrilateral inscribed in one of them and tangent to the other if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
their radii satisfy
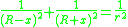
where x is the distance between their centers. This condition is known as Fuss' theorem.
Regular polygons
For all regular polygons, x=0. That is, the incircle and the circumcircle share a common center. This center is also the center of the regular polygon.For some regular polygons which can be constructed with compass and ruler, we have the following formulas for the relation between the common edge
Edge (geometry)
In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....
length a, the radius r of the incircle
Incircle and excircles of a triangle
In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides...
, and the radius R of the circumcircle:
 |
 |
 |
 |
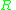| 3 |  |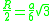
 |
 |
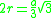| 4 Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... |
 |
 |
 |
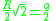| 5 Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... |
 |
 |
 |
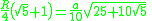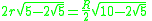| 6 |  |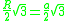
 |
 |
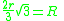| 8 |  |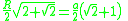
 |
 |
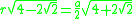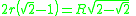| 10 Decagon In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°... |
 |
 |
 |
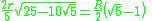