
Configuration state function
Encyclopedia
In quantum chemistry
, a configuration state function (CSF), is a symmetry-adapted linear combination of Slater determinant
s. A CSF must not be confused with a configuration
.
, a configuration state function (CSF), is a symmetry-adapted linear combination of Slater determinant
s. It is constructed to have the same quantum numbers as the wavefunction,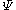 , of the system being studied. In the method of configuration interaction
, of the system being studied. In the method of configuration interaction
the wavefunction can be expressed as a linear combination of CSFs, that is in the form
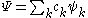
where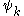 denotes the set of CSFs. The coefficients,
denotes the set of CSFs. The coefficients, 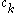 , are found by using the expansion of
, are found by using the expansion of 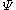 to compute a Hamiltonian matrix. When this is diagonalized, the eigenvectors are chosen as the expansion coefficients. CSFs rather than just Slater determinants can also be used as a basis in Multi-configurational self-consistent field
to compute a Hamiltonian matrix. When this is diagonalized, the eigenvectors are chosen as the expansion coefficients. CSFs rather than just Slater determinants can also be used as a basis in Multi-configurational self-consistent field
computations.
In atomic structure, a CSF is an eigenstate of
In linear molecules, does not commute with the Hamiltonian for the system and therefore CSFs are not eigenstates of
does not commute with the Hamiltonian for the system and therefore CSFs are not eigenstates of 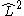 . However, the z-projection of angular momentum is still a good quantum number and CSFs are constructed to be eigenstates of
. However, the z-projection of angular momentum is still a good quantum number and CSFs are constructed to be eigenstates of 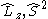 and
and 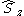 . In non-linear (which implies polyatomic) molecules, neither
. In non-linear (which implies polyatomic) molecules, neither 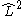 nor
nor 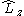 commute with the Hamiltonian. The CSFs are constructed to have the spatial transformation properties of one of the irreducible representations of the point group to which the nuclear framework belongs. This is because the Hamiltonian operator transforms in the same way.
commute with the Hamiltonian. The CSFs are constructed to have the spatial transformation properties of one of the irreducible representations of the point group to which the nuclear framework belongs. This is because the Hamiltonian operator transforms in the same way. 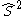 and
and 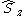 are still valid quantum numbers and CSFs are built to be eigenfunctions of these operators.
are still valid quantum numbers and CSFs are built to be eigenfunctions of these operators.
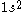 and
and 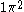 are example of two configurations, one from atomic structure and one from molecular structure.
are example of two configurations, one from atomic structure and one from molecular structure.
From any given configuration we can, in general, create several CSFs. CSFs are therefore sometimes also called N-particle symmetry adapted basis functions. It is important to realize that for a configuration the number of electrons is fixed; let's call this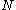 . When we are creating CSFs from a configuration we have to work with the spin-orbitals associated with the configuration.
. When we are creating CSFs from a configuration we have to work with the spin-orbitals associated with the configuration.
For example given the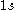 orbital in an atom we know that there are two spin-orbitals associated with this,
orbital in an atom we know that there are two spin-orbitals associated with this,

where

are the one electron spin-eigenfunctions for spin-up and spin-down respectively. Similarly, for the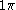 orbital in a linear molecule (
orbital in a linear molecule (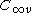 point group) we have four spin orbitals:
point group) we have four spin orbitals:
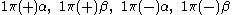 .
.
This is because the designation corresponds to z-projection of angular momentum of both
designation corresponds to z-projection of angular momentum of both 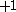 and
and 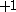 .
.
We can think of the set of spin orbitals as a set of boxes each of size one; let's call this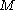 boxes. We distribute the
boxes. We distribute the 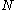 electrons among the
electrons among the 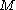 boxes in all possible ways. Each assignment corresponds to one Slater determinant,
boxes in all possible ways. Each assignment corresponds to one Slater determinant, 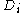 . There can be great number of these, particularly when
. There can be great number of these, particularly when  . Another way to look at this is to say we have
. Another way to look at this is to say we have  entities and we wish to select
entities and we wish to select 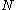 of them, known as a combination
of them, known as a combination
. We need to find all possible combinations. Order of the selection is not significant because we are working with determinants and can interchange rows as required.
If we then specify the overall coupling that we wish to achieve for the configuration, we can now select only those Slater determinants that have the required quantum numbers. In order to achieve the required total spin angular momentum (and in the case of atoms the total orbital angular momentum as well), each Slater determinant has to be premultiplied by a coupling coefficient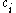 , derived ultimately from Clebsch-Gordan coefficients
, derived ultimately from Clebsch-Gordan coefficients
. Thus the CSF is a linear combination
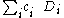 .
.
The Lowdin projection operator formalism may be used to find the coefficients. For any given set of determinants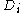 it may be possible to find several different sets of coefficients. Each set corresponds to one CSF. In fact this simply reflects the different internal couplings of total spin and spatial angular momentum.
it may be possible to find several different sets of coefficients. Each set corresponds to one CSF. In fact this simply reflects the different internal couplings of total spin and spatial angular momentum.
and
using the following genealogical algorithm:
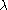 value for each orbital; for molecules whose nuclear framework transforms according to
value for each orbital; for molecules whose nuclear framework transforms according to 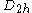 symmetry, or one of its sub-groups, the group product table has to be used to find the product of the irreducible representation of all
symmetry, or one of its sub-groups, the group product table has to be used to find the product of the irreducible representation of all 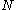 orbitals.
orbitals.
The above steps will need to be repeated many times to elucidate the total set of CSFs that can be derived from
the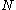 electrons and
electrons and 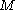 orbitals.
orbitals.
these will be provided either as a table or thourgh a set of logic statements.
The following table shows the possible couplings for a orbital with one or two
orbital with one or two
electrons.
The next table shows the fifteen possible couplings for a orbital.
orbital.
The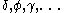 orbitals also each generate fiftenn possible
orbitals also each generate fiftenn possible
couplings, all of which can be easily inferred from this table.
Similar tables can be constructed for atomic systems, which transform according to the point group of the sphere,
that is for s, p, d, f orbitals. The number of term sysmbols and therefore possible couplings
orbitals. The number of term sysmbols and therefore possible couplings
is significantly larger in the atomic case.
Quantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
, a configuration state function (CSF), is a symmetry-adapted linear combination of Slater determinant
Slater determinant
In quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
s. A CSF must not be confused with a configuration
Electron configuration
In atomic physics and quantum chemistry, electron configuration is the arrangement of electrons of an atom, a molecule, or other physical structure...
.
Definition
In quantum chemistryQuantum chemistry
Quantum chemistry is a branch of chemistry whose primary focus is the application of quantum mechanics in physical models and experiments of chemical systems...
, a configuration state function (CSF), is a symmetry-adapted linear combination of Slater determinant
Slater determinant
In quantum mechanics, a Slater determinant is an expression that describes the wavefunction of a multi-fermionic system that satisfies anti-symmetry requirements and consequently the Pauli exclusion principle by changing sign upon exchange of fermions . It is named for its discoverer, John C...
s. It is constructed to have the same quantum numbers as the wavefunction,
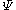 , of the system being studied. In the method of configuration interaction
, of the system being studied. In the method of configuration interactionConfiguration interaction
Configuration interaction is a post-Hartree–Fock linear variational method for solving the nonrelativistic Schrödinger equation within the Born–Oppenheimer approximation for a quantum chemical multi-electron system. Mathematically, configuration simply describes the linear combination...
the wavefunction can be expressed as a linear combination of CSFs, that is in the form
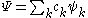
where
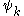 denotes the set of CSFs. The coefficients,
denotes the set of CSFs. The coefficients, 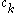 , are found by using the expansion of
, are found by using the expansion of 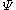 to compute a Hamiltonian matrix. When this is diagonalized, the eigenvectors are chosen as the expansion coefficients. CSFs rather than just Slater determinants can also be used as a basis in Multi-configurational self-consistent field
to compute a Hamiltonian matrix. When this is diagonalized, the eigenvectors are chosen as the expansion coefficients. CSFs rather than just Slater determinants can also be used as a basis in Multi-configurational self-consistent fieldMulti-configurational self-consistent field
Multi-configurational self-consistent field is a method in quantum chemistry used to generate qualitatively correct reference states of molecules in cases where Hartree–Fock and density functional theory are not adequate...
computations.
In atomic structure, a CSF is an eigenstate of
- the square of the angular momentum operator,
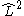 .
. - the z-projection of angular momentum
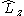
- the square of the spin operatorSpin (physics)In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
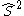 .
. - the z-projection of the spin operator

In linear molecules,
 does not commute with the Hamiltonian for the system and therefore CSFs are not eigenstates of
does not commute with the Hamiltonian for the system and therefore CSFs are not eigenstates of 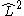 . However, the z-projection of angular momentum is still a good quantum number and CSFs are constructed to be eigenstates of
. However, the z-projection of angular momentum is still a good quantum number and CSFs are constructed to be eigenstates of 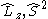 and
and 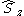 . In non-linear (which implies polyatomic) molecules, neither
. In non-linear (which implies polyatomic) molecules, neither 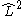 nor
nor 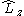 commute with the Hamiltonian. The CSFs are constructed to have the spatial transformation properties of one of the irreducible representations of the point group to which the nuclear framework belongs. This is because the Hamiltonian operator transforms in the same way.
commute with the Hamiltonian. The CSFs are constructed to have the spatial transformation properties of one of the irreducible representations of the point group to which the nuclear framework belongs. This is because the Hamiltonian operator transforms in the same way. 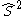 and
and 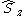 are still valid quantum numbers and CSFs are built to be eigenfunctions of these operators.
are still valid quantum numbers and CSFs are built to be eigenfunctions of these operators.From Configurations to Configuration State Functions
CSFs are however derived from configurations. A configuration is just an assignment of electrons to orbitals. For example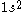 and
and 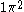 are example of two configurations, one from atomic structure and one from molecular structure.
are example of two configurations, one from atomic structure and one from molecular structure.From any given configuration we can, in general, create several CSFs. CSFs are therefore sometimes also called N-particle symmetry adapted basis functions. It is important to realize that for a configuration the number of electrons is fixed; let's call this
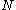 . When we are creating CSFs from a configuration we have to work with the spin-orbitals associated with the configuration.
. When we are creating CSFs from a configuration we have to work with the spin-orbitals associated with the configuration.For example given the
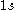 orbital in an atom we know that there are two spin-orbitals associated with this,
orbital in an atom we know that there are two spin-orbitals associated with this,
where

are the one electron spin-eigenfunctions for spin-up and spin-down respectively. Similarly, for the
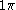 orbital in a linear molecule (
orbital in a linear molecule (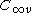 point group) we have four spin orbitals:
point group) we have four spin orbitals: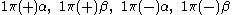 .
.This is because the
 designation corresponds to z-projection of angular momentum of both
designation corresponds to z-projection of angular momentum of both 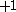 and
and 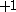 .
.We can think of the set of spin orbitals as a set of boxes each of size one; let's call this
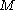 boxes. We distribute the
boxes. We distribute the 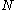 electrons among the
electrons among the 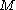 boxes in all possible ways. Each assignment corresponds to one Slater determinant,
boxes in all possible ways. Each assignment corresponds to one Slater determinant, 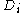 . There can be great number of these, particularly when
. There can be great number of these, particularly when  . Another way to look at this is to say we have
. Another way to look at this is to say we have  entities and we wish to select
entities and we wish to select 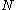 of them, known as a combination
of them, known as a combinationCombination
In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...
. We need to find all possible combinations. Order of the selection is not significant because we are working with determinants and can interchange rows as required.
If we then specify the overall coupling that we wish to achieve for the configuration, we can now select only those Slater determinants that have the required quantum numbers. In order to achieve the required total spin angular momentum (and in the case of atoms the total orbital angular momentum as well), each Slater determinant has to be premultiplied by a coupling coefficient
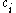 , derived ultimately from Clebsch-Gordan coefficients
, derived ultimately from Clebsch-Gordan coefficientsClebsch-Gordan coefficients
In physics, the Clebsch–Gordan coefficients are sets of numbers that arise in angular momentum coupling under the laws of quantum mechanics.In more mathematical terms, the CG coefficients are used in representation theory, particularly of compact Lie groups, to perform the explicit direct sum...
. Thus the CSF is a linear combination
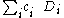 .
.The Lowdin projection operator formalism may be used to find the coefficients. For any given set of determinants
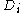 it may be possible to find several different sets of coefficients. Each set corresponds to one CSF. In fact this simply reflects the different internal couplings of total spin and spatial angular momentum.
it may be possible to find several different sets of coefficients. Each set corresponds to one CSF. In fact this simply reflects the different internal couplings of total spin and spatial angular momentum.A genealogical algorithm for CSF construction
At the most fundamental level, a configuration state function can be constructed- from a set of
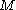 orbitals
orbitals
and
- a number
 of electrons
of electrons
using the following genealogical algorithm:
- distribute the
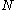 over the set of
over the set of 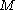 orbitals giving a configuration
orbitals giving a configuration - for each orbital the possible quantum number couplings (and therefore wavefunctions for the individual orbitals) are known from basic quantum mechanics; for each orbital choose one of the permitted couplings but leave the z-component of the total spin,
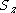 undefined.
undefined. - check that the spatial coupling of all orbitals matches that required for the system wavefunction. For a molecule exhibiting
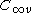 or
or  this is achieved by a simple linear summation of the coupled
this is achieved by a simple linear summation of the coupled
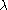 value for each orbital; for molecules whose nuclear framework transforms according to
value for each orbital; for molecules whose nuclear framework transforms according to 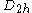 symmetry, or one of its sub-groups, the group product table has to be used to find the product of the irreducible representation of all
symmetry, or one of its sub-groups, the group product table has to be used to find the product of the irreducible representation of all 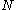 orbitals.
orbitals.
- couple the total spins of the
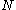 orbitals from left to right; this means we have to choose a fixed
orbitals from left to right; this means we have to choose a fixed 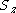 for each orbital.
for each orbital. - test the final total spin and its z-projection against the values required for the system wavefunction
The above steps will need to be repeated many times to elucidate the total set of CSFs that can be derived from
the
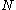 electrons and
electrons and 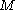 orbitals.
orbitals.Single Orbital configurations and wavefunctions
Basic quantum mechanics defines the possible single orbital wavefunctions. In any software implementation,these will be provided either as a table or thourgh a set of logic statements.
The following table shows the possible couplings for a
 orbital with one or two
orbital with one or twoelectrons.
| Orbital Configuration | Term symbol |  projection projection |
|---|---|---|
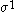 |
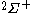 |
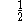 |
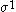 |
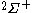 |
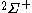 |
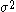 |
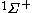 |
 |
The next table shows the fifteen possible couplings for a
 orbital.
orbital.The
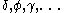 orbitals also each generate fiftenn possible
orbitals also each generate fiftenn possiblecouplings, all of which can be easily inferred from this table.
| Orbital Configuration | Term symbol | Lambda coupling | 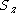 projection projection |
|---|---|---|---|
 |
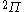 |
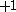 |
 |
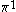 |
 |
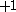 |
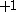 |
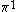 |
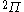 |
 |
 |
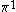 |
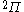 |
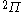 |
 |
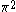 |
 |
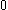 |
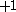 |
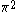 |
 |
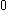 |
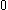 |
 |
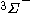 |
 |
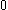 |
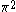 |
 |
 |
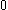 |
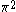 |
 |
 |
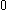 |
 |
 |
 |
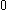 |
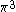 |
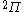 |
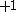 |
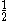 |
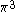 |
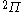 |
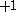 |
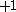 |
 |
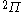 |
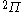 |
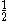 |
 |
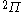 |
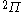 |
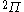 |
 |
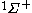 |
 |
 |
Similar tables can be constructed for atomic systems, which transform according to the point group of the sphere,
that is for s, p, d, f
 orbitals. The number of term sysmbols and therefore possible couplings
orbitals. The number of term sysmbols and therefore possible couplingsis significantly larger in the atomic case.

