
Conformal gravity
Encyclopedia
Conformal gravity is a generic name for gravity theories which are invariant under conformal transformations
in the Riemannian geometry
sense; more accurately, they are invariant under Weyl transformations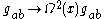 where
where  is the metric tensor
is the metric tensor
and is a function on spacetime
is a function on spacetime
.
as the Lagrangian
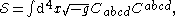
where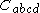 is the Weyl tensor. This is to be contrasted with the usual Einstein–Hilbert action where the Lagrangian is just the Ricci scalar
is the Weyl tensor. This is to be contrasted with the usual Einstein–Hilbert action where the Lagrangian is just the Ricci scalar
. The equation of motion upon varying the metric is called the Bach equation,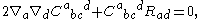
where is the Ricci tensor
is the Ricci tensor
. Conformally flat metrics are solutions of this equation.
Since these theories lead to fourth order equations for the fluctuations around a fixed background, they are not manifestly unitary. It has therefore been generally believed that they could not be consistently quantized. This is now disputed .
theory. This means that each term in the wave equation can contain up to 4 derivatives. There are pros and cons of 4-derivative theories. The pros are that the quantized version of the theory is more convergent and renormalisable
. The cons are that there may be issues with causality. A simpler example of a 4-derivative wave equation is the scalar 4-derivative wave equation:

The solution for this is in a central field of force is:
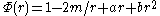
The first two terms are the same as a normal wave equation. Since this equation is a simpler approximation to Conformal gravity then m corresponds to mass of the central source. The last two terms are unique to 4-derivative wave equations. It has been suggested to assign small values to them to account for the galactic acceleration constant (also known as dark matter
) and the dark energy
constant .
The main issue with conformal gravity theories, as well as any theory with higher derivatives, is the typical presence of ghosts, which point to instabilities of the quantum version of the theory, although there might be a solution to the ghost problem .
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
in the Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
sense; more accurately, they are invariant under Weyl transformations
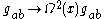 where
where  is the metric tensor
is the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
and
 is a function on spacetime
is a function on spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
.
Weyl-squared theories
The simplest theory in this category has the square of the Weyl tensorWeyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
as the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
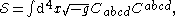
where
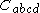 is the Weyl tensor. This is to be contrasted with the usual Einstein–Hilbert action where the Lagrangian is just the Ricci scalar
is the Weyl tensor. This is to be contrasted with the usual Einstein–Hilbert action where the Lagrangian is just the Ricci scalarScalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
. The equation of motion upon varying the metric is called the Bach equation,
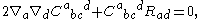
where
 is the Ricci tensor
is the Ricci tensorRicci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
. Conformally flat metrics are solutions of this equation.
Since these theories lead to fourth order equations for the fluctuations around a fixed background, they are not manifestly unitary. It has therefore been generally believed that they could not be consistently quantized. This is now disputed .
Four derivative theories
Conformal gravity is an example of a 4-derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
theory. This means that each term in the wave equation can contain up to 4 derivatives. There are pros and cons of 4-derivative theories. The pros are that the quantized version of the theory is more convergent and renormalisable
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
. The cons are that there may be issues with causality. A simpler example of a 4-derivative wave equation is the scalar 4-derivative wave equation:

The solution for this is in a central field of force is:
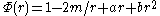
The first two terms are the same as a normal wave equation. Since this equation is a simpler approximation to Conformal gravity then m corresponds to mass of the central source. The last two terms are unique to 4-derivative wave equations. It has been suggested to assign small values to them to account for the galactic acceleration constant (also known as dark matter
Dark matter
In astronomy and cosmology, dark matter is matter that neither emits nor scatters light or other electromagnetic radiation, and so cannot be directly detected via optical or radio astronomy...
) and the dark energy
Dark energy
In physical cosmology, astronomy and celestial mechanics, dark energy is a hypothetical form of energy that permeates all of space and tends to accelerate the expansion of the universe. Dark energy is the most accepted theory to explain recent observations that the universe appears to be expanding...
constant .
The main issue with conformal gravity theories, as well as any theory with higher derivatives, is the typical presence of ghosts, which point to instabilities of the quantum version of the theory, although there might be a solution to the ghost problem .

