
Congruent number
Encyclopedia
In mathematics
, a congruent number is a positive integer
that is the area of a right triangle
with three rational number
sides. A more general definition includes all positive rational numbers with this property.
The sequence of integer congruent numbers starts with
For example, 5 is a congruent number because it is the area of a 20/3, 3/2, 41/6 triangle. Similarly, 6 is a congruent number because it is the area of a 3,4,5 triangle. 3 is not a congruent number.
If q is a congruent number then s2q is also a congruent number for any rational number s (just by multiplying each side of the triangle by s). This leads to the observation that whether a nonzero rational number q is a congruent number depends only on its residue in the group
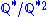 .
.
Every residue class in this group contains exactly one square free integer, and it is common, therefore, only to consider square free positive integers, when speaking about congruent numbers.
provides an easily testable criterion for determining whether a number is congruent; but his result relies on the Birch and Swinnerton-Dyer conjecture
, which is still unproven.
Fermat's right triangle theorem, named after Pierre de Fermat
, states that no square number
can be a congruent number.
has positive rank
. An alternative approach to the idea is presented below (as can essentially also be found in the introduction to Tunnell's paper).
Suppose a,b,c are numbers (not necessarily positive or rational) which satisfy the following two equations:
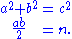
Then set x = n(a+c)/b and
y = 2n2(a+c)/b2.
A calculation shows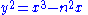
and y is not 0 (if y = 0 then a = -c, so b = 0, but (1/2)ab = n is nonzero, a contradiction).
Conversely, if x and y are numbers which satisfy the above equation and y is not 0, set
a = (x2 - n2)/y,
b = 2nx/y, and c = (x2 + n2)/y . A calculation shows these three numbers
satisfy the two equations for a, b, and c above.
These two correspondences between (a,b,c) and (x,y) are inverses of each other, so
we have a one-to-one correspondence between any solution of the two equations in
a, b, and c and any solution of the equation in x and y with y nonzero. In particular,
from the formulas in the two correspondences, for rational n we see that a, b, and c are
rational if and only if the corresponding x and y are rational, and vice versa.
(We also have that a, b, and c are all positive if and only if x and y are all positive;
notice from the equation y2 = x3 - xn2 = x(x2 - n2)
that if x and y are positive then x2 - n2 must be positive, so the formula for
a above is positive.)
Thus a positive rational number n is congruent if and only if the equation
y2 = x3 - n2x has a rational point with y not equal to 0.
It can be shown (as a nice application of Dirichlet's theorem
on primes in arithmetic progression)
that the only torsion points on this elliptic curve are those with y equal to 0, hence the
existence of a rational point with y nonzero is equivalent to saying the elliptic curve has positive rank.
For example, it is known that if p is a prime number then
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a congruent number is a positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
that is the area of a right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
with three rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
sides. A more general definition includes all positive rational numbers with this property.
The sequence of integer congruent numbers starts with
- 5, 6, 7, 13, 14, 15, 20, 21, 22, 23, 24, 28, 29, 30, 31, 34, 37, 38, 39, 41, 45, 46, 47, …
For example, 5 is a congruent number because it is the area of a 20/3, 3/2, 41/6 triangle. Similarly, 6 is a congruent number because it is the area of a 3,4,5 triangle. 3 is not a congruent number.
If q is a congruent number then s2q is also a congruent number for any rational number s (just by multiplying each side of the triangle by s). This leads to the observation that whether a nonzero rational number q is a congruent number depends only on its residue in the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
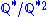 .
.Every residue class in this group contains exactly one square free integer, and it is common, therefore, only to consider square free positive integers, when speaking about congruent numbers.
Congruent number problem
The question of determining whether a given rational number is a congruent number is called the congruent number problem. This problem has not (as of 2009) been brought to a successful resolution. Tunnell's theoremTunnell's theorem
In number theory, Tunnell's theorem gives a partial resolution to the congruent number problem, and under the Birch and Swinnerton-Dyer conjecture, a full resolution. The congruent number problem asks which rational numbers can be the area of a right triangle with all three sides rational...
provides an easily testable criterion for determining whether a number is congruent; but his result relies on the Birch and Swinnerton-Dyer conjecture
Birch and Swinnerton-Dyer conjecture
In mathematics, the Birch and Swinnerton-Dyer conjecture is an open problem in the field of number theory. Its status as one of the most challenging mathematical questions has become widely recognized; the conjecture was chosen as one of the seven Millennium Prize Problems listed by the Clay...
, which is still unproven.
Fermat's right triangle theorem, named after Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
, states that no square number
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
can be a congruent number.
Relation to elliptic curves
The question of whether a given number is congruent turns out to be equivalent to the condition that a certain elliptic curveElliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
has positive rank
Rank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
. An alternative approach to the idea is presented below (as can essentially also be found in the introduction to Tunnell's paper).
Suppose a,b,c are numbers (not necessarily positive or rational) which satisfy the following two equations:
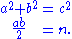
Then set x = n(a+c)/b and
y = 2n2(a+c)/b2.
A calculation shows
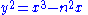
and y is not 0 (if y = 0 then a = -c, so b = 0, but (1/2)ab = n is nonzero, a contradiction).
Conversely, if x and y are numbers which satisfy the above equation and y is not 0, set
a = (x2 - n2)/y,
b = 2nx/y, and c = (x2 + n2)/y . A calculation shows these three numbers
satisfy the two equations for a, b, and c above.
These two correspondences between (a,b,c) and (x,y) are inverses of each other, so
we have a one-to-one correspondence between any solution of the two equations in
a, b, and c and any solution of the equation in x and y with y nonzero. In particular,
from the formulas in the two correspondences, for rational n we see that a, b, and c are
rational if and only if the corresponding x and y are rational, and vice versa.
(We also have that a, b, and c are all positive if and only if x and y are all positive;
notice from the equation y2 = x3 - xn2 = x(x2 - n2)
that if x and y are positive then x2 - n2 must be positive, so the formula for
a above is positive.)
Thus a positive rational number n is congruent if and only if the equation
y2 = x3 - n2x has a rational point with y not equal to 0.
It can be shown (as a nice application of Dirichlet's theorem
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
on primes in arithmetic progression)
that the only torsion points on this elliptic curve are those with y equal to 0, hence the
existence of a rational point with y nonzero is equivalent to saying the elliptic curve has positive rank.
Current progress
Much work has been done classifying congruent numbers.For example, it is known that if p is a prime number then
- if p ≡ 3 (modModular arithmeticIn mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
8), then p is not a congruent number, but 2p is a congruent number. - if p ≡ 5 (mod 8), then p is a congruent number.
- if p ≡ 7 (mod 8), then p and 2p are congruent numbers.

