Conjugacy problem
Encyclopedia
In abstract algebra
, the conjugacy problem for a group
G with a given presentation
is the decision problem
of determining, given two words x and y in G, whether or not they represent conjugate
elements of G. That is, the problem is to determine whether there exists an element z of G such that
The conjugacy problem is also known as the transformation problem.
The conjugacy problem was identified by Max Dehn
in 1911 as one of the fundamental decision problems in group theory; the other two being the word problem
and the isomorphism problem
. The conjugacy problem contains the word problem as a special case: if x and y are words, deciding if they are the same word is equivalent to deciding if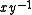
is the identity, which is the same as deciding if it's conjugate to the identity. In 1912 Dehn gave an algorithm that solves both the word and conjugacy problem for the fundamental group
s of closed orientable two-dimensional manifolds of genus greater than or equal to 2 (the genus 0 and genus 1 cases being trivial).
It is known that the conjugacy problem is undecidable
for many classes of groups.
Classes of group presentations for which it is known to be soluble include:
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the conjugacy problem for a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G with a given presentation
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
is the decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
of determining, given two words x and y in G, whether or not they represent conjugate
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
elements of G. That is, the problem is to determine whether there exists an element z of G such that
The conjugacy problem is also known as the transformation problem.
The conjugacy problem was identified by Max Dehn
Max Dehn
Max Dehn was a German American mathematician and a student of David Hilbert. He is most famous for his work in geometry, topology and geometric group theory...
in 1911 as one of the fundamental decision problems in group theory; the other two being the word problem
Word problem for groups
In mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
and the isomorphism problem
Group isomorphism problem
In abstract algebra, the group isomorphism problem is the decision problem of determining whether two group presentations present isomorphic groups....
. The conjugacy problem contains the word problem as a special case: if x and y are words, deciding if they are the same word is equivalent to deciding if
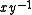is the identity, which is the same as deciding if it's conjugate to the identity. In 1912 Dehn gave an algorithm that solves both the word and conjugacy problem for the fundamental groupFundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
s of closed orientable two-dimensional manifolds of genus greater than or equal to 2 (the genus 0 and genus 1 cases being trivial).
It is known that the conjugacy problem is undecidable
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
for many classes of groups.
Classes of group presentations for which it is known to be soluble include:
- free groups (no defining relators)
- one-relator groups with torsion
- finitely presented conjugacy separable groups
- finitely generated abelian groups (relators include all commutators)
- Gromov-hyperbolic groupsHyperbolic groupIn group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
- CAT(0) groups