Consequences of special relativity
Encyclopedia
Special relativity
has several consequences that struck many people as counterintuitive, among which are:
Imagine a clock that measured time by bouncing a photon (a particle of light) between two mirrors that are its walls, say "horizontally". The photon must always travel at the speed of light
(c). Even when the clock is moving (at velocity
), the light photon must move at exactly the speed of light. Now if the direction the clock is moving is "vertical" (perpendicular to the original path of the photon), the photon's velocity can be represented by a vector whose direction is the hypotenuse of the right triangle formed by the horizontal (
) and vertical (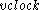
) components. Since the length of this hypotenuse (the resultant velocity) must not exceed c, the "horizontal" speed of the photon (the length of 
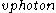) will be less than c. This can be determined using the Pythagorean theorem
(
):
which can be solved as:
.
To check, substituting 0 for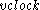
makes:
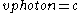(which makes sense).
If the distance between the clock mirrors were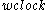
and the clock were not moving, then based on the definition of speed, the photon would travel once between the mirrors in the amount of time, 
, given by:
.
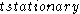is the time interval measured by the stationary clock—its basic unit (or "tick" interval).
However, if the clock were moving, then the "horizontal" speed of the photon towards the opposite mirror (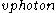
) calculated above would be 
. Hence, the time interval measured by the moving clock will be:
(Note that the above works because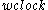
is the ("horizontal") width of the clock in a dimension in which it is not moving, and the clock's width is not relativistically affected by the movement in an orthogonal dimension.)
Since we want to know the effect of moving the clock on its basic time interval, we rearrange the equation,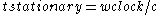
to:
and substitute that into the equation above to get:
.
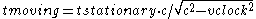can be factored out of the denominator by factoring the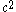 
out of the 
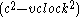to get 
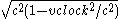which leads to 
.
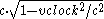The
's in the numerator and the denominator then cancel out to make
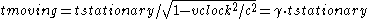
where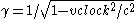
is known as the Lorentz factor
.
This means that the faster the clock moves, the longer its "tick interval" relative to a stationary clock. In effect, time measured by the moving clock has slowed down!
Extrapolating this, because all motion is relative, if ship A is moving relative to ship B, occupants of ship A see the time of occupants of ship B running slow and occupants of ship B see the time of occupants of ship A running slow. There is no logical or experimental way of saying which occupants are "right", so they can both be said to be correct.
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
has several consequences that struck many people as counterintuitive, among which are:
- The time lapse between two events is not invariant from one observer to another, but is dependent on the relative speeds of the observers' reference frames. (See Lorentz transformation equations.)
- Two events that occur simultaneously in different places in one frame of reference may occur at different times in another frame of reference (lack of absolute simultaneity).
- The dimensions (e.g. length, see Length contractionLength contractionIn physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
and Special relativity#Time dilation and length contraction) of an object as measured by one observer may differ from the results of measurements of the same object made by another observer. (See Lorentz transformation equations.) - The twin paradoxTwin paradoxIn physics, the twin paradox is a thought experiment in special relativity, in which a twin makes a journey into space in a high-speed rocket and returns home to find he has aged less than his identical twin who stayed on Earth...
concerns a twin who flies off in a spaceship traveling near the speed of light. When he returns he discovers that his twin has aged much more rapidly than he has (or he aged more slowly). - The ladder paradoxLadder paradoxThe ladder paradox is a thought experiment in special relativity. It involves a ladder travelling horizontally and undergoing a length contraction, the result of which being that it can fit into a much smaller garage...
involves a long ladder traveling near the speed of light and being contained within a smaller garage. - Velocities do not combine by simple addition, but instead by a relativistic velocity addition formulaVelocity-addition formulaIn physics, a velocity-addition formula is an equation that relates the velocities of moving objects in different reference frames.- Galilean addition of velocities :...
. - Fast moving objects will appear to be distorted by Terrell rotationTerrell rotationTerrell rotation is the name of a mathematical and physical effect. Specifically, Terrell rotation is the distortion that a passing object would appear to undergo, according to the special theory of relativity if it were travelling a significant fraction of the speed of light...
. - The inability for matter or information to travel faster-than-lightFaster-than-lightFaster-than-light communications and travel refer to the propagation of information or matter faster than the speed of light....
.
The effect on time
The assumption that light travels at a constant speed in a vacuum has a distinct effect on time.Imagine a clock that measured time by bouncing a photon (a particle of light) between two mirrors that are its walls, say "horizontally". The photon must always travel at the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
(c). Even when the clock is moving (at velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
), the light photon must move at exactly the speed of light. Now if the direction the clock is moving is "vertical" (perpendicular to the original path of the photon), the photon's velocity can be represented by a vector whose direction is the hypotenuse of the right triangle formed by the horizontal () and vertical (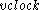) components. Since the length of this hypotenuse (the resultant velocity) must not exceed c, the "horizontal" speed of the photon (the length of 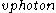) will be less than c. This can be determined using the Pythagorean theoremPythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
(
):which can be solved as:
.To check, substituting 0 for
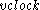makes: 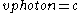(which makes sense).If the distance between the clock mirrors were
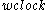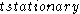and the clock were not moving, then based on the definition of speed, the photon would travel once between the mirrors in the amount of time, , given by: . is the time interval measured by the stationary clock—its basic unit (or "tick" interval).However, if the clock were moving, then the "horizontal" speed of the photon towards the opposite mirror (
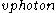) calculated above would be . Hence, the time interval measured by the moving clock will be:(Note that the above works because
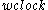is the ("horizontal") width of the clock in a dimension in which it is not moving, and the clock's width is not relativistically affected by the movement in an orthogonal dimension.)Since we want to know the effect of moving the clock on its basic time interval, we rearrange the equation,
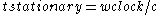to:and substitute that into the equation above to get:
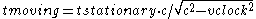. can be factored out of the denominator by factoring the 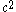out of the 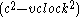to get 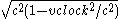which leads to 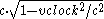.The
's in the numerator and the denominator then cancel out to make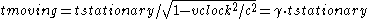where
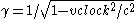is known as the Lorentz factorLorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
.
This means that the faster the clock moves, the longer its "tick interval" relative to a stationary clock. In effect, time measured by the moving clock has slowed down!
Extrapolating this, because all motion is relative, if ship A is moving relative to ship B, occupants of ship A see the time of occupants of ship B running slow and occupants of ship B see the time of occupants of ship A running slow. There is no logical or experimental way of saying which occupants are "right", so they can both be said to be correct.
See also
- Simultaneity
- Time dilation and length contraction
- Causality and prohibition of motion faster than light