Constant Q transform
Encyclopedia
In mathematics and signal processing
, the Constant Q Transform transforms a data series to the frequency domain, and is related to the Fourier Transform
.
The transform can be thought of as a series of logarithmically spaced filters, with the k-th filter having a spectral width some multiple of the previous filter's width, i.e.
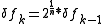
Where we have n filters per octave
of frequency. This recursive relationship can be rewritten as:
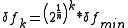
where fmin is the centre frequency of the first bin used.
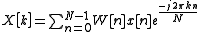
Given a data series, sampled at
, T being the sampling period of our data, for each frequency bin we can define the following:
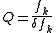
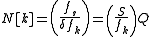
As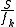
is the number of samples processed per cycle at frequency fk, Q is the number of integer cycles processed at this center frequency.
The equivalent transform kernel can be found by using the following substitutions:
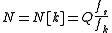
After these modifications, we are left with:
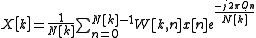
(FFT). However, the FFT can itself be employed, in conjunction with the use of a kernel
, to perform the equivalent calculation but much faster .
The transform mirrors the human auditory system, whereby at lower frequencies spectral resolution is better, whereas temporal resolution improves at higher frequencies, and so for musical data this is a reasonable trade off.
In addition, the harmonics of musical notes form a pattern characteristic of the timbre of the instrument in this transform. Assuming the same relative strengths of each harmonic, as the fundamental frequency changes, the relative position of these harmonics remains constant. This can make identification of instruments much easier.
Relative to the Fourier Transform, implementation of this transform is more tricky. This is due to the varying number of samples used in the calculation of each frequency bin, which also affects the length of any windowing function implemented.
Also note that because the frequency scale is logarithmic, there is no true zero-frequency / DC term present, perhaps limiting possible utility of the transform.
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, the Constant Q Transform transforms a data series to the frequency domain, and is related to the Fourier Transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
.
The transform can be thought of as a series of logarithmically spaced filters, with the k-th filter having a spectral width some multiple of the previous filter's width, i.e.
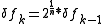
Where we have n filters per octave
Octave (electronics)
In electronics, an octave is a doubling or halving of a frequency. The term is derived from the musical octave which similarly describes such frequency ratios, but the prefix octa-, denoting eight, has no significance in physics...
of frequency. This recursive relationship can be rewritten as:
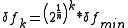
where fmin is the centre frequency of the first bin used.
Calculation of the Transform
The short-time Fourier Transform is calculated as follows: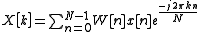Given a data series, sampled at
, T being the sampling period of our data, for each frequency bin we can define the following:- Filter width,
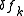
- Q, the "quality factor". This is shown below to be the integer number of cycles processed at a center frequency fk. As such, this somewhat defines the time complexity of the transform.
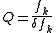
- Window length for the k-th bin
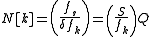
As
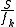is the number of samples processed per cycle at frequency fk, Q is the number of integer cycles processed at this center frequency.The equivalent transform kernel can be found by using the following substitutions:
- The window length of each bin is now a function of the bin number:
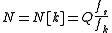
- The relative power of each bin will decrease with higher frequencies, as these sum over fewer terms. To compensate for this, we normalize by N[k].
- Any windowing function will be a function of window length, and likewise a function of window number. For example, the equivalent Hamming window would be,
- Our digital frequency,
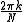, becomes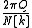 
After these modifications, we are left with:
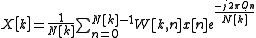
Fast calculation using FFT
The direct calculation of the Constant Q transform is slow when compared against the Fast Fourier TransformFast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT). However, the FFT can itself be employed, in conjunction with the use of a kernel
Kernel (statistics)
A kernel is a weighting function used in non-parametric estimation techniques. Kernels are used in kernel density estimation to estimate random variables' density functions, or in kernel regression to estimate the conditional expectation of a random variable. Kernels are also used in time-series,...
, to perform the equivalent calculation but much faster .
Comparison with the Fourier Transform
In general, the transform is well suited to musical data, and this can be seen in some of its advantages compared to the Fast Fourier Transform. As the output of the transform is effectively amplitude/phase against log frequency, fewer frequency bins are required to cover a given range effectively, and this proves useful where frequencies span several octaves. As the range of human hearing covers approximately ten octaves from 20 Hz to around 20 kHz, this reduction in output data is significant. The downside of this is a reduction in frequency resolution with higher frequency bins.The transform mirrors the human auditory system, whereby at lower frequencies spectral resolution is better, whereas temporal resolution improves at higher frequencies, and so for musical data this is a reasonable trade off.
In addition, the harmonics of musical notes form a pattern characteristic of the timbre of the instrument in this transform. Assuming the same relative strengths of each harmonic, as the fundamental frequency changes, the relative position of these harmonics remains constant. This can make identification of instruments much easier.
Relative to the Fourier Transform, implementation of this transform is more tricky. This is due to the varying number of samples used in the calculation of each frequency bin, which also affects the length of any windowing function implemented.
Also note that because the frequency scale is logarithmic, there is no true zero-frequency / DC term present, perhaps limiting possible utility of the transform.