Continuous function (set theory)
Encyclopedia
In mathematics
, specifically set theory
, a continuous function is a sequence of ordinal
s such that the values assumed at limit stages are the limits (limit suprema and limit infima
) of all values at previous stages. More formally, let γ be an ordinal, and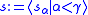
be a γ-sequence of ordinals. Then s is continuous if at every limit ordinal β < γ,
and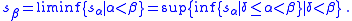
Alternatively, s is continuous if s: γ → range(s) is a continuous function when the sets are each equipped with the order topology
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a continuous function is a sequence of ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s such that the values assumed at limit stages are the limits (limit suprema and limit infima
Limit superior and limit inferior
In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence...
) of all values at previous stages. More formally, let γ be an ordinal, and
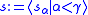be a γ-sequence of ordinals. Then s is continuous if at every limit ordinal β < γ,and
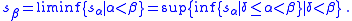
Alternatively, s is continuous if s: γ → range(s) is a continuous function when the sets are each equipped with the order topology
Order topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
.