
Contortion tensor
Encyclopedia
The contorsion tensor in differential geometry expresses the difference between a metric-compatible affine connection
with Christoffel symbol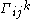 and the unique torsion-free Levi-Civita connection
and the unique torsion-free Levi-Civita connection
for the same metric.
The contortion tensor is defined in terms of the torsion tensor
is defined in terms of the torsion tensor
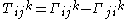 as
as
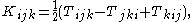
where the indices are being raised and lowered with respect to the metric:
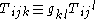 .
.
The reason for the non-obvious sum in the definition is that the contortion tensor, being the difference between two metric-compatible Christoffel symbols, must be antisymmetric in the last two indices, whilst the torsion tensor itself is antisymmetric in its first two indices.
The connection can now be written as
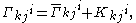
where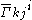 is the torsion-free Levi-Civita connection.
is the torsion-free Levi-Civita connection.
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
with Christoffel symbol
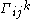 and the unique torsion-free Levi-Civita connection
and the unique torsion-free Levi-Civita connectionLevi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
for the same metric.
The contortion tensor
 is defined in terms of the torsion tensor
is defined in terms of the torsion tensorTorsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
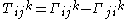 as
as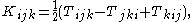
where the indices are being raised and lowered with respect to the metric:
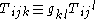 .
.The reason for the non-obvious sum in the definition is that the contortion tensor, being the difference between two metric-compatible Christoffel symbols, must be antisymmetric in the last two indices, whilst the torsion tensor itself is antisymmetric in its first two indices.
The connection can now be written as
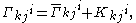
where
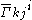 is the torsion-free Levi-Civita connection.
is the torsion-free Levi-Civita connection.

