Coordinate time
Encyclopedia
In the theory of relativity
, it is convenient to express results in terms of a spacetime
coordinate system
relative to an implied observer
. In many (but not all) coordinate systems, an event
is specified by one time
coordinate and three spatial coordinates. The time specified by the time coordinate is referred to as coordinate time to distinguish it from proper time
.
In the special case of an inertial observer in special relativity
, by convention the coordinate time at an event is the same as the proper time
measured by a clock that is at the same location as the event, that is stationary relative to the observer and that has been synchronised to the observer's clock using the Einstein synchronisation
convention.
For non-inertial observers, and in general relativity
, coordinate systems can be chosen more freely. For a clock whose spatial coordinates are constant, the relationship between proper time
(tau) and coordinate time 
, i.e. the rate of time dilation
, is given by
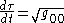. . . . . .(1),
where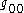
is a component of the metric tensor
, which incorporates gravitational time dilation
(under the assumption that the zeroth component is timelike).
An alternative formulation, correct to the order of terms in 1/c2, gives the relation between proper and coordinate time in terms of more-easily recognizable quantities in dynamics:
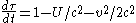. . . . . .(2)
in which: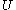
represents a sum GMi/ri of gravitational potentials due to the masses in the neighborhood, based on their distances ri from the clock. This sum of the GMi/ri is evaluated approximately, as a sum of Newtonian gravitational potentials (plus any tidal potentials considered), and is represented using the positive astronomical sign convention for gravitational potentials;
is the velocity of light;
is the (scalar) velocity of the clock (in the coordinates of the chosen reference frame) defined by: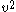
= (dx2 + dy2 + dz2)/dtc2 . . . . . .(3)
Equation (2) is a fundamental and much-quoted differential equation for the relation between proper time and coordinate time, i.e. for time dilation. A derivation, starting from the Schwarzschild metric
, with further reference sources, is given in Time dilation due to gravitation and motion together.
and give rise to a limited concept of simultaneity
.
Two events are called simultaneous in a chosen reference frame if and only if the chosen coordinate time has the same value for both of them; and this condition allows for the physical possibility and likelihood that they will not be simultaneous from the standpoint of another reference frame.
But the coordinate time is not a time that could be measured by a clock located at the place that nominally defines the reference frame, e.g. a clock located at the solar system barycenter would not measure the coordinate time of the barycentric reference frame, and a clock located at the geocenter would not measure the coordinate time of a geocentric reference frame. The coordinate times cannot be measured, but only computed from the (proper-time) readings of real clocks with the aid of the time dilation relationship shown in equation (2) (or some alternative or refined form of it).
Only for explanatory purposes it is possible to conceive a hypothetical observer and trajectory on which the proper time of the clock would coincide with coordinate time: such an observer and clock have to be conceived at rest with respect to the chosen reference frame (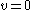
in equation (2) above) but also (in an unattainably hypothetical situation) infinitely far away from its gravitational masses (also 
in equation (2) above). Even such an illustration is of limited use because the coordinate time is defined everywhere in the reference frame, while the hypothetical observer and clock chosen to illustrate it has only a limited choice of trajectory.
designed for use as the time coordinate in calculations that need to take account of relativistic effects. The choice of a time coordinate implies the choice of an entire frame of reference.
As described above, a time coordinate can to a limited extent be illustrated by the proper time of a clock that is notionally infinitely far away from the objects of interest and at rest with respect to the chosen reference frame. This notional clock, because it is outside all gravity well
s, is not influenced by gravitational time dilation
. The proper time of objects within a gravity well will pass more slowly than the coordinate time even when they are at rest with respect to the coordinate reference frame. Gravitational as well as motional time dilation must be considered for each object of interest, and the effects are functions of the velocity relative to the reference frame and of the gravitational potential as indicated in equation (2) above.
There are four purpose-designed coordinate time scales defined by the IAU
for use in astronomy
. Barycentric Coordinate Time
(TCB) is based on a reference frame comoving with the barycenter
of the Solar system
, and has been defined for use in calculating motion of bodies within the Solar system. However, from the standpoint of Earth-based observers, general time dilation including gravitational time dilation causes Barycentric Coordinate Time, which is based on the SI second, to appear when observed from the Earth to have time units that pass more quickly than SI seconds measured by an Earth-based clock, with a rate of divergence of about 0.5 seconds per year. Accordingly, for many practical astronomical purposes, a scaled modification of TCB has been defined, called for historical reasons Barycentric Dynamical Time
(TDB), with a time unit that evaluates to SI seconds when observed from the Earth's surface, thus assuring that at least for several millennia TDB will remain within 2 milliseconds of Terrestrial Time
(TT), albeit that the time unit of TDB, if measured by the hypothetical observer described above, at rest in the reference frame and at infinite distance, would be very slightly slower than the SI second (by 1 part in 1/LB = 1 part in 108/1.550519768).
Geocentric Coordinate Time
(TCG) is based on a reference frame comoving with the geocenter (the center of the Earth), and is defined in principle for use for calculations concerning phenomena on or in the region of the Earth, such as planetary rotation and satellite
motions. To a much smaller extent than with TCB compared with TDB, but for a corresponding reason, the SI second of TCG when observed from the Earth's surface shows a slight acceleration on the SI seconds realized by Earth-surface-based clocks. Accordingly, Terrestrial Time
(TT) has also been defined as a scaled version of TCG, with the scaling such that on the defined geoid the unit rate is equal to the SI second, albeit that in terms of TCG the SI second of TT is a very little slower (this time by 1 part in 1/LG = 1 part in 1010/6.969290134).
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
, it is convenient to express results in terms of a spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
relative to an implied observer
Observer (special relativity)
The term observer in special relativity refers most commonly to an inertial reference frame. Less often it may refer to an arbitrary non-inertial reference frame; in particular, a Rindler frame is sometimes called an "accelerating observer". In such cases an inertial reference frame may be called...
. In many (but not all) coordinate systems, an event
Event (relativity)
In physics, and in particular relativity, an event indicates a physical situation or occurrence, located at a specific point in space and time. For example, a glass breaking on the floor is an event; it occurs at a unique place and a unique time, in a given frame of reference.Strictly speaking, the...
is specified by one time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
coordinate and three spatial coordinates. The time specified by the time coordinate is referred to as coordinate time to distinguish it from proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
.
In the special case of an inertial observer in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, by convention the coordinate time at an event is the same as the proper time
Proper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
measured by a clock that is at the same location as the event, that is stationary relative to the observer and that has been synchronised to the observer's clock using the Einstein synchronisation
Einstein synchronisation
Einstein synchronisation is a convention for synchronising clocks at different places by means of signal exchanges. This synchronisation method was used already by telegraphers in the middle 19th century, but was popularized by H. Poincaré and A...
convention.
For non-inertial observers, and in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, coordinate systems can be chosen more freely. For a clock whose spatial coordinates are constant, the relationship between proper time
(tau) and coordinate time , i.e. the rate of time dilationTime dilation
In the theory of relativity, time dilation is an observed difference of elapsed time between two events as measured by observers either moving relative to each other or differently situated from gravitational masses. An accurate clock at rest with respect to one observer may be measured to tick at...
, is given by
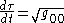. . . . . .(1),where
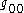is a component of the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
, which incorporates gravitational time dilation
Gravitational time dilation
Gravitational time dilation is the effect of time passing at different rates in regions of different gravitational potential; the lower the gravitational potential, the more slowly time passes...
(under the assumption that the zeroth component is timelike).
An alternative formulation, correct to the order of terms in 1/c2, gives the relation between proper and coordinate time in terms of more-easily recognizable quantities in dynamics:
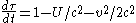. . . . . .(2)in which:
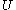represents a sum GMi/ri of gravitational potentials due to the masses in the neighborhood, based on their distances ri from the clock. This sum of the GMi/ri is evaluated approximately, as a sum of Newtonian gravitational potentials (plus any tidal potentials considered), and is represented using the positive astronomical sign convention for gravitational potentials; is the velocity of light; is the (scalar) velocity of the clock (in the coordinates of the chosen reference frame) defined by: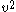 = (dx2 + dy2 + dz2)/dtc2 . . . . . .(3)
- and dx, dy, dz and dtc are small increments in three orthogonal space-like coordinates x, y, z and in the coordinate time tc of the clock's position in the chosen reference frame.
Equation (2) is a fundamental and much-quoted differential equation for the relation between proper time and coordinate time, i.e. for time dilation. A derivation, starting from the Schwarzschild metric
Schwarzschild metric
In Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
, with further reference sources, is given in Time dilation due to gravitation and motion together.
Coordinate time, proper time, and clock synchronization
Fuller explanation of the concept of coordinate time comes from its relationships with proper time and with clock synchronization. Synchronization, along with the related concept of simultaneity, has to receive careful definition in the framework of general relativity theory, because many of the assumptions inherent in classical mechanics and classical accounts of space and time had to be removed. Specific clock synchronization procedures were defined by EinsteinAlbert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
and give rise to a limited concept of simultaneity
Relativity of simultaneity
In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...
.
Two events are called simultaneous in a chosen reference frame if and only if the chosen coordinate time has the same value for both of them; and this condition allows for the physical possibility and likelihood that they will not be simultaneous from the standpoint of another reference frame.
But the coordinate time is not a time that could be measured by a clock located at the place that nominally defines the reference frame, e.g. a clock located at the solar system barycenter would not measure the coordinate time of the barycentric reference frame, and a clock located at the geocenter would not measure the coordinate time of a geocentric reference frame. The coordinate times cannot be measured, but only computed from the (proper-time) readings of real clocks with the aid of the time dilation relationship shown in equation (2) (or some alternative or refined form of it).
Only for explanatory purposes it is possible to conceive a hypothetical observer and trajectory on which the proper time of the clock would coincide with coordinate time: such an observer and clock have to be conceived at rest with respect to the chosen reference frame (
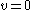in equation (2) above) but also (in an unattainably hypothetical situation) infinitely far away from its gravitational masses (also in equation (2) above). Even such an illustration is of limited use because the coordinate time is defined everywhere in the reference frame, while the hypothetical observer and clock chosen to illustrate it has only a limited choice of trajectory.Coordinate time scales
A coordinate time scale (or coordinate time standard) is a time standardTime standard
A time standard is a specification for measuring time: either the rate at which time passes; or points in time; or both. In modern times, several time specifications have been officially recognized as standards, where formerly they were matters of custom and practice. An example of a kind of time...
designed for use as the time coordinate in calculations that need to take account of relativistic effects. The choice of a time coordinate implies the choice of an entire frame of reference.
As described above, a time coordinate can to a limited extent be illustrated by the proper time of a clock that is notionally infinitely far away from the objects of interest and at rest with respect to the chosen reference frame. This notional clock, because it is outside all gravity well
Gravity well
A gravity well or gravitational well is a conceptual model of the gravitational field surrounding a body in space. The more massive the body the deeper and more extensive the gravity well associated with it. The Sun has a far-reaching and deep gravity well. Asteroids and small moons have much...
s, is not influenced by gravitational time dilation
Gravitational time dilation
Gravitational time dilation is the effect of time passing at different rates in regions of different gravitational potential; the lower the gravitational potential, the more slowly time passes...
. The proper time of objects within a gravity well will pass more slowly than the coordinate time even when they are at rest with respect to the coordinate reference frame. Gravitational as well as motional time dilation must be considered for each object of interest, and the effects are functions of the velocity relative to the reference frame and of the gravitational potential as indicated in equation (2) above.
There are four purpose-designed coordinate time scales defined by the IAU
IAU
IAU may refer to:*International Astronomical Union*International American University*International American University College of Medicine*International Association of Universities*International Association of Ultrarunners...
for use in astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
. Barycentric Coordinate Time
Barycentric Coordinate Time
Barycentric Coordinate Time is a coordinate time standard intended to be used as the independent variable of time for all calculations pertaining to orbits of planets, asteroids, comets, and interplanetary spacecraft in the Solar system...
(TCB) is based on a reference frame comoving with the barycenter
Barycentric coordinates (astronomy)
In astronomy, barycentric coordinates are non-rotating coordinates with origin at the center of mass of two or more bodies.The barycenter is the point between two objects where they balance each other. For example, it is the center of mass where two or more celestial bodies orbit each other...
of the Solar system
Solar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
, and has been defined for use in calculating motion of bodies within the Solar system. However, from the standpoint of Earth-based observers, general time dilation including gravitational time dilation causes Barycentric Coordinate Time, which is based on the SI second, to appear when observed from the Earth to have time units that pass more quickly than SI seconds measured by an Earth-based clock, with a rate of divergence of about 0.5 seconds per year. Accordingly, for many practical astronomical purposes, a scaled modification of TCB has been defined, called for historical reasons Barycentric Dynamical Time
Barycentric Dynamical Time
Barycentric Dynamical Time is a relativistic coordinate time scale, intended for astronomical use as a time standard to take account of time dilation when calculating orbits and astronomical ephemerides of planets, asteroids, comets and interplanetary spacecraft in the Solar system...
(TDB), with a time unit that evaluates to SI seconds when observed from the Earth's surface, thus assuring that at least for several millennia TDB will remain within 2 milliseconds of Terrestrial Time
Terrestrial Time
Terrestrial Time is a modern astronomical time standard defined by the International Astronomical Union, primarily for time-measurements of astronomical observations made from the surface of the Earth....
(TT), albeit that the time unit of TDB, if measured by the hypothetical observer described above, at rest in the reference frame and at infinite distance, would be very slightly slower than the SI second (by 1 part in 1/LB = 1 part in 108/1.550519768).
Geocentric Coordinate Time
Geocentric Coordinate Time
Geocentric Coordinate Time is a coordinate time standard intended to be used as the independent variable of time for all calculations pertaining to precession, nutation, the Moon, and artificial satellites of the Earth...
(TCG) is based on a reference frame comoving with the geocenter (the center of the Earth), and is defined in principle for use for calculations concerning phenomena on or in the region of the Earth, such as planetary rotation and satellite
Satellite
In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
motions. To a much smaller extent than with TCB compared with TDB, but for a corresponding reason, the SI second of TCG when observed from the Earth's surface shows a slight acceleration on the SI seconds realized by Earth-surface-based clocks. Accordingly, Terrestrial Time
Terrestrial Time
Terrestrial Time is a modern astronomical time standard defined by the International Astronomical Union, primarily for time-measurements of astronomical observations made from the surface of the Earth....
(TT) has also been defined as a scaled version of TCG, with the scaling such that on the defined geoid the unit rate is equal to the SI second, albeit that in terms of TCG the SI second of TT is a very little slower (this time by 1 part in 1/LG = 1 part in 1010/6.969290134).