Einstein synchronisation
Encyclopedia
Einstein synchronisation (or Poincaré–Einstein synchronisation) is a convention
for synchronising clocks at different places by means of signal exchanges. This synchronisation method was used already by telegraphers in the middle 19th century, but was popularized by H. Poincaré and A. Einstein who applied it to light signals and recognized its fundamental role in relativity theory
. Its principal value is for clocks within a single inertial frame.
's prescription from 1905, a light signal is sent at time
from clock 1 to clock 2 and immediately back, e.g. by means of a mirror. Its arrival time back at clock 1 is 
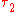. This synchronisation convention sets clock 2 so that the time of signal reflection is 
.
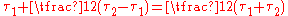The same synchronisation is achieved by "slowly" transporting a third clock from clock 1 to clock 2, in the limit of vanishing transport velocity. The literature discusses many other thought experiments for clock synchronisation giving the same result.
The problem is whether this synchronisation does really succeed in assigning a time label to any event in a consistent way. To that end one should find conditions under which
(a) clocks once synchronised remain synchronised,
(b1) the synchronisation is reflexive
, that is any clock is synchronised with itself (automatically satisfied),
(b2) the synchronisation is symmetric
, that is if clock A is synchronised with clock B then clock B is synchronised with clock A,
(b3) the synchronisation is transitive
, that is if clock A is synchronised with clock B and clock B is synchronised with clock C then clock A is synchronised with clock C.
If point (a) holds then it makes sense to say that clocks are synchronised. Given (a), if (b1)–(b3) hold then the synchronisation allows us to build a global time function t. The slices t=const. are called "simultaneity slices".
Einstein (1905) did not recognize the possibility of reducing (a) and (b1)–(b3) to easily verifiable physical properties of light propagation (see below). Instead he just wrote "We assume that this definition of synchronism is free from contradictions, and possible for any number of points; and that the following [that is (b2)–(b3)] relations are universally valid." For this reason, and since posterior developments are not so well known, some physical papers still present the assumption of consistency of Einstein synchronisation among the postulates of relativity theory.
L. Silberstein was the first to study the problem of the consistency of Einstein's synchronisation although he left most of his claims as an exercise for the readers of his textbook on relativity. His arguments were taken up again by H. Reichenbach, and found a final shape in a work by A. Macdonald. The solution is that the Einstein synchronisation satisfies the previous requirements if and only if the following two conditions hold
(i) [no redshift:] If from point A two flashes are emitted after a time interval Dt as recorded by a clock at A, then they reach B separated by a time interval Dt as recorded by a clock at B.
(ii) [Reichenbach's round-trip condition:] If a light beam is sent over the triangle ABC, starting from A (and through reflection with mirrors at B and C) then the event of return at A is independent of the direction followed (ABCA or ACBA).
Once clocks are synchronised one can measure the one-way light speed. However, the previous conditions that guarantee the applicability of Einstein's synchronisation do not imply that the one-way light speed turns out to be the same all over the frame. Consider the condition
(iii) [Weyl's round-trip condition:] The time needed by a light beam to traverse a closed path of length L is L/c, where L is the length of the path and c is a constant independent of the path.
A theorem whose origin can be traced back to H. Weyl, states that the Weyl's round trip condition holds if and only if the Einstein synchronisation can be applied consistently (i.e. (a) and (b1)–(b3) hold) and the one-way speed of light with respect to the so synchronised clocks is a constant all over the frame. The importance of Weyl's condition stands on the fact that the time there mentioned can be measured with only one clock thus this condition does not rely on synchronisation conventions and can be experimentally checked. Indeed, it is experimentally verified that the Weyl round-trip condition holds in the inertial frames.
Since it is meaningless to measure a one-way velocity prior to the synchronisation of distant clocks, experiments claiming a measure of the one-way speed of light can often be reinterpreted as verifying the Weyl's round-trip condition.
The Einstein synchronisation looks this natural only in inertial frames. One can easily forget that it is only a convention. In rotating frames, even in special relativity, the non-transitivity of Einstein synchronisation diminishes its usefulness. If clock 1 and clock 2 are not synchronised directly, but by using a chain of intermediate clocks, the synchronisation depends on the path chosen. Synchronisation around the circumference of a rotating disk gives a non vanishing time difference that depends on the direction used. This is important in the Sagnac effect
and the Ehrenfest paradox
. The Global Positioning System
accounts for this effect.
A substantive discussion of Einstein synchronisation's conventionalism is due to Reichenbach
. Most attempts to negate the conventionality of this synchronisation are considered refuted, with the notable exception of Malament
's argument, that it can be derived from demanding a symmetrical relation of causal connectibility. Whether this settles the issue is disputed.
. In 1898 (in a philosophical paper) he argued that the postulate of light speed constancy in all directions is useful to formulate physical laws in a simple way. He also showed that the definition of simultaneity of events at different places is only a convention. Based on those conventions, but within the framework of the now superseded aether theory
, Poincaré in 1900 proposed the following convention for defining clock synchronisation: 2 observers A and B, which are moving in the aether, synchronise their clocks by means of optical signals. Because of the relativity principle they believe to be at rest in the aether and assume that the speed of light is constant in all directions. Therefore they have to consider only the transmission time of the signals and then crossing their observations to examine whether their clocks are synchronous.
In 1904 Poincaré illustrated the same procedure in the following way:
Convention (norm)
A convention is a set of agreed, stipulated or generally accepted standards, norms, social norms or criteria, often taking the form of a custom....
for synchronising clocks at different places by means of signal exchanges. This synchronisation method was used already by telegraphers in the middle 19th century, but was popularized by H. Poincaré and A. Einstein who applied it to light signals and recognized its fundamental role in relativity theory
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
. Its principal value is for clocks within a single inertial frame.
Einstein
According to Albert EinsteinAlbert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's prescription from 1905, a light signal is sent at time
from clock 1 to clock 2 and immediately back, e.g. by means of a mirror. Its arrival time back at clock 1 is 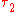. This synchronisation convention sets clock 2 so that the time of signal reflection is 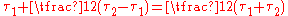.The same synchronisation is achieved by "slowly" transporting a third clock from clock 1 to clock 2, in the limit of vanishing transport velocity. The literature discusses many other thought experiments for clock synchronisation giving the same result.
The problem is whether this synchronisation does really succeed in assigning a time label to any event in a consistent way. To that end one should find conditions under which
(a) clocks once synchronised remain synchronised,
(b1) the synchronisation is reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
, that is any clock is synchronised with itself (automatically satisfied),
(b2) the synchronisation is symmetric
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
, that is if clock A is synchronised with clock B then clock B is synchronised with clock A,
(b3) the synchronisation is transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, that is if clock A is synchronised with clock B and clock B is synchronised with clock C then clock A is synchronised with clock C.
If point (a) holds then it makes sense to say that clocks are synchronised. Given (a), if (b1)–(b3) hold then the synchronisation allows us to build a global time function t. The slices t=const. are called "simultaneity slices".
Einstein (1905) did not recognize the possibility of reducing (a) and (b1)–(b3) to easily verifiable physical properties of light propagation (see below). Instead he just wrote "We assume that this definition of synchronism is free from contradictions, and possible for any number of points; and that the following [that is (b2)–(b3)] relations are universally valid." For this reason, and since posterior developments are not so well known, some physical papers still present the assumption of consistency of Einstein synchronisation among the postulates of relativity theory.
L. Silberstein was the first to study the problem of the consistency of Einstein's synchronisation although he left most of his claims as an exercise for the readers of his textbook on relativity. His arguments were taken up again by H. Reichenbach, and found a final shape in a work by A. Macdonald. The solution is that the Einstein synchronisation satisfies the previous requirements if and only if the following two conditions hold
(i) [no redshift:] If from point A two flashes are emitted after a time interval Dt as recorded by a clock at A, then they reach B separated by a time interval Dt as recorded by a clock at B.
(ii) [Reichenbach's round-trip condition:] If a light beam is sent over the triangle ABC, starting from A (and through reflection with mirrors at B and C) then the event of return at A is independent of the direction followed (ABCA or ACBA).
Once clocks are synchronised one can measure the one-way light speed. However, the previous conditions that guarantee the applicability of Einstein's synchronisation do not imply that the one-way light speed turns out to be the same all over the frame. Consider the condition
(iii) [Weyl's round-trip condition:] The time needed by a light beam to traverse a closed path of length L is L/c, where L is the length of the path and c is a constant independent of the path.
A theorem whose origin can be traced back to H. Weyl, states that the Weyl's round trip condition holds if and only if the Einstein synchronisation can be applied consistently (i.e. (a) and (b1)–(b3) hold) and the one-way speed of light with respect to the so synchronised clocks is a constant all over the frame. The importance of Weyl's condition stands on the fact that the time there mentioned can be measured with only one clock thus this condition does not rely on synchronisation conventions and can be experimentally checked. Indeed, it is experimentally verified that the Weyl round-trip condition holds in the inertial frames.
Since it is meaningless to measure a one-way velocity prior to the synchronisation of distant clocks, experiments claiming a measure of the one-way speed of light can often be reinterpreted as verifying the Weyl's round-trip condition.
The Einstein synchronisation looks this natural only in inertial frames. One can easily forget that it is only a convention. In rotating frames, even in special relativity, the non-transitivity of Einstein synchronisation diminishes its usefulness. If clock 1 and clock 2 are not synchronised directly, but by using a chain of intermediate clocks, the synchronisation depends on the path chosen. Synchronisation around the circumference of a rotating disk gives a non vanishing time difference that depends on the direction used. This is important in the Sagnac effect
Sagnac effect
The Sagnac effect , named after French physicist Georges Sagnac, is a phenomenon encountered in interferometry that is elicited by rotation. The Sagnac effect manifests itself in a setup called ring interferometry. A beam of light is split and the two beams are made to follow a trajectory in...
and the Ehrenfest paradox
Ehrenfest paradox
The Ehrenfest paradox concerns the rotation of a "rigid" disc in the theory of relativity.In its original formulation as presented by Paul Ehrenfest 1909 in the Physikalische Zeitschrift, it discusses an ideally rigid cylinder that is made to rotate about its axis of symmetry...
. The Global Positioning System
Global Positioning System
The Global Positioning System is a space-based global navigation satellite system that provides location and time information in all weather, anywhere on or near the Earth, where there is an unobstructed line of sight to four or more GPS satellites...
accounts for this effect.
A substantive discussion of Einstein synchronisation's conventionalism is due to Reichenbach
Hans Reichenbach
Hans Reichenbach was a leading philosopher of science, educator and proponent of logical empiricism...
. Most attempts to negate the conventionality of this synchronisation are considered refuted, with the notable exception of Malament
David B. Malament
David B. Malament is an American philosopher of science.He attended Stuyvesant High School and received a B.A. in mathematics 1968 at Columbia College and Ph.D. in philosophy 1975 at Rockefeller University...
's argument, that it can be derived from demanding a symmetrical relation of causal connectibility. Whether this settles the issue is disputed.
History: Poincaré
Some features of the conventionality of synchronization were anticipated by Henri PoincaréHenri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
. In 1898 (in a philosophical paper) he argued that the postulate of light speed constancy in all directions is useful to formulate physical laws in a simple way. He also showed that the definition of simultaneity of events at different places is only a convention. Based on those conventions, but within the framework of the now superseded aether theory
Lorentz ether theory
What is now often called Lorentz Ether theory has its roots in Hendrik Lorentz's "Theory of electrons", which was the final point in the development of the classical aether theories at the end of the 19th and at the beginning of the 20th century....
, Poincaré in 1900 proposed the following convention for defining clock synchronisation: 2 observers A and B, which are moving in the aether, synchronise their clocks by means of optical signals. Because of the relativity principle they believe to be at rest in the aether and assume that the speed of light is constant in all directions. Therefore they have to consider only the transmission time of the signals and then crossing their observations to examine whether their clocks are synchronous.
In 1904 Poincaré illustrated the same procedure in the following way:
Literature
- D. DieksDennis DieksDennis Dieks is a Dutch physicist and philosopher of physics. In 1982 he proved the no-cloning theorem . In 1989 he proposed a new interpretation of quantum mechanics, later known as a version of the modal interpretation of quantum mechanics...
, Becoming, relativity and locality, in The Ontology of Spacetime, online - D. DieksDennis DieksDennis Dieks is a Dutch physicist and philosopher of physics. In 1982 he proved the no-cloning theorem . In 1989 he proposed a new interpretation of quantum mechanics, later known as a version of the modal interpretation of quantum mechanics...
(ed.), The Ontology of Spacetime, Elsevier 2006, ISBN 0-444-52768-0 - D. Malament, 1977. "Causal Theories of Time and the Conventionality of Simultaniety," Noûs 11, 293–300.
- Galison, P. (2003), Einstein's Clocks, Poincaré's Maps: Empires of Time, New York: W.W. Norton, ISBN 0393326047
- A. Grünbaum. David Malament and the Conventionality of Simultaneity: A Reply, online
- S. Sarkar, J. Stachel, Did Malament Prove the Non-Conventionality of Simultaneity in the Special Theory of Relativity?, Philosophy of Science, Vol. 66, No. 2
- H. Reichenbach, Axiomatization of the theory of relativity, Berkeley University Press, 1969
- H. Reichenbach, The philosophy of space & time, Dover, New York, 1958
- H. P. Robertson, Postulate versus Observation in the Special Theory of Relativity, Reviews of Modern Physics, 1949
- R. Rynasiewicz, Definition, Convention, and Simultaneity: Malament's Result and Its Alleged Refutation by Sarkar and Stachel, Philosophy of Science, Vol. 68, No. 3, Supplement, online
- Hanoch Ben-Yami, Causality and Temporal Order in Special Relativity, British Jnl. for the Philosophy of Sci., Volume 57, Number 3, pp. 459–479, abstract online
External links
- Stanford Encyclopedia of Philosophy, Conventionality of Simultaneity http://plato.stanford.edu/entries/spacetime-convensimul/ (contains extensive bibliography)
- Neil Ashby, Relativity in the Global Positioning System, Living Rev. Relativity 6, (2003), http://www.livingreviews.org/lrr-2003-1
- How to Calibrate a Perfect Clock from John de Pillis: An interactive Flash animation showing how a clock with uniform ticking rate can precisely define a one-second time interval.
- Synchronizing Five Clocks from John de Pillis. An interactive Flash animation showing how five clocks are synchronised within a single inertial frame.
See also
- Relativity of simultaneityRelativity of simultaneityIn physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...
- One-way speed of lightOne-way speed of lightThe "one-way" speed of light from a source to a detector, cannot be measured independently of a convention as to how to synchronize the clocks at the source and the detector. What can however be experimentally measured is the round-trip speed from the source to the detector and back again...