Ehrenfest paradox
Encyclopedia
The Ehrenfest paradox
concerns the rotation of a "rigid" disc in the theory of relativity
.
In its original formulation as presented by Paul Ehrenfest
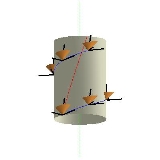
1909 in the Physikalische Zeitschrift, it discusses an ideally rigid cylinder that is made to rotate about its axis of symmetry. The radius R as seen in the laboratory frame is always perpendicular to its motion and should therefore be equal to its value R0 when stationary. However, the circumference (2πR) should appear Lorentz-contracted
to a smaller value than at rest, by the usual factor γ. This leads to the contradiction that R=R0 and R0.
(Note that a cylinder was considered in order to circumvent the possibility of a disc "dishing" out of its plane of rotation
and trivially satisfying C<2πR. Subsequently when a rotating disc is substituted it is assumed that this distortion possibility is also excluded).
The paradox has been deepened further by later reasoning that since measuring rods aligned along the periphery and moving with it should appear contracted, more would fit around the circumference, which would thus measure greater than 2πR.
The Ehrenfest paradox may be the most basic phenomenon in relativity that has a long history marked by controversy and which still gets different interpretations published in peer-reviewed journals.
Any rigid object made from real materials, which is rotating with the transverse velocity
close to the speed of sound
in this material, must exceed the point of rupture due to centrifugal force
because centrifugal pressure
can not exceed shear modulus of material
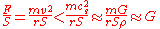
where is speed of sound,
is speed of sound,  is density and
is density and  is shear modulus. Thus, in the case of speed of light
is shear modulus. Thus, in the case of speed of light
, is only a thought experiment
. Neutron-degenerate matter
allows velocities close to speed of light, because e.g. the speed of neutron-star oscillations
is relativistic, however these bodies can not be said to be "rigid".
 .
.
Let us fix the reference frame to the stationary center of the disk. Then the magnitude of the relative velocity of any point in the circumference of the disk is . So the circumference will undergo Lorentz contraction by a factor of
. So the circumference will undergo Lorentz contraction by a factor of  .
.
However the radius being perpendicular to the direction of motion, will not undergo any contraction. So we have
 . This is paradoxical, since Euclidean geometry
. This is paradoxical, since Euclidean geometry
tells us it should be exactly equal to .
.
cylinder that is made to rotate. Assuming that the cylinder does not expand or contract, its radius stays the same. But measuring rods laid out along the circumference should be Lorentz-contracted to a smaller value than at rest, by the usual factor γ. This leads to the paradox that the rigid measuring rods would have to separate from one another due to Lorentz contraction; the discrepancy noted by Ehrenfest seems to suggest that a rotated Born rigid disk should shatter.
should be Lorentz-contracted to a smaller value than at rest, by the usual factor γ. This leads to the paradox that the rigid measuring rods would have to separate from one another due to Lorentz contraction; the discrepancy noted by Ehrenfest seems to suggest that a rotated Born rigid disk should shatter.
Thus Ehrenfest argued by reductio ad absurdum
that Born rigidity
is not generally compatible with special relativity. It's worth mentioning that according to special relativity an object cannot be spun up from a non-rotating state while maintaining Born rigidity, but once it has achieved a constant nonzero angular velocity it does maintain Born rigidity without violating special relativity, and then (as Einstein later showed) a disk riding observer will measure a circumference:
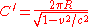 .
.
which is available on-line.
The modern resolution can be briefly summarized as follows:
preprints which repeat various long-corrected errors originally made by earlier authors), we can identify a number of major conceptual errors which are common to many incorrect claims which have been made over the years concerning "the geometry of a rotating disk":
Although the theory to resolve the paradox was understood by 1937, many subsequent authors have repeated various conceptual errors which had already been cleared up in earlier work, possibly because some of the explanations were not quite explicit.
Some other "paradoxes" in special relativity
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
concerns the rotation of a "rigid" disc in the theory of relativity
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
.
In its original formulation as presented by Paul Ehrenfest
Paul Ehrenfest
Paul Ehrenfest was an Austrian and Dutch physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem.- Biography :Paul Ehrenfest was born and grew up in Vienna in a Jewish...
1909 in the Physikalische Zeitschrift, it discusses an ideally rigid cylinder that is made to rotate about its axis of symmetry. The radius R as seen in the laboratory frame is always perpendicular to its motion and should therefore be equal to its value R0 when stationary. However, the circumference (2πR) should appear Lorentz-contracted
Length contraction
In physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
to a smaller value than at rest, by the usual factor γ. This leads to the contradiction that R=R0 and R
(Note that a cylinder was considered in order to circumvent the possibility of a disc "dishing" out of its plane of rotation
Plane of rotation
In geometry, a plane of rotation is an abstract object used to describe or visualise rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.Mathematically such...
and trivially satisfying C<2πR. Subsequently when a rotating disc is substituted it is assumed that this distortion possibility is also excluded).
The paradox has been deepened further by later reasoning that since measuring rods aligned along the periphery and moving with it should appear contracted, more would fit around the circumference, which would thus measure greater than 2πR.
The Ehrenfest paradox may be the most basic phenomenon in relativity that has a long history marked by controversy and which still gets different interpretations published in peer-reviewed journals.
Any rigid object made from real materials, which is rotating with the transverse velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
close to the speed of sound
Speed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
in this material, must exceed the point of rupture due to centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
because centrifugal pressure
Specific strength
The specific strength is a material's strength divided by its density. It is also known as the strength-to-weight ratio or strength/weight ratio. In fiber or textile applications, tenacity is the usual measure of specific strength...
can not exceed shear modulus of material
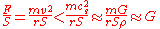
where
 is speed of sound,
is speed of sound,  is density and
is density and  is shear modulus. Thus, in the case of speed of light
is shear modulus. Thus, in the case of speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, is only a thought experiment
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
. Neutron-degenerate matter
Degenerate matter
Degenerate matter is matter that has such extraordinarily high density that the dominant contribution to its pressure is attributable to the Pauli exclusion principle. The pressure maintained by a body of degenerate matter is called the degeneracy pressure, and arises because the Pauli principle...
allows velocities close to speed of light, because e.g. the speed of neutron-star oscillations
Neutron-star oscillations
Asteroseismology studies the internal structure of our Sun and other stars using oscillations. These can be studied by interpreting the temporal frequency spectrum acquired through observations...
is relativistic, however these bodies can not be said to be "rigid".
Essence of the paradox
Imagine a disk of radius R rotating with constant angular velocity .
.Let us fix the reference frame to the stationary center of the disk. Then the magnitude of the relative velocity of any point in the circumference of the disk is
 . So the circumference will undergo Lorentz contraction by a factor of
. So the circumference will undergo Lorentz contraction by a factor of  .
.However the radius being perpendicular to the direction of motion, will not undergo any contraction. So we have
 . This is paradoxical, since Euclidean geometry
. This is paradoxical, since Euclidean geometryEuclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
tells us it should be exactly equal to
 .
.Ehrenfest's argument
Ehrenfest considered an ideally Born rigidRigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
cylinder that is made to rotate. Assuming that the cylinder does not expand or contract, its radius stays the same. But measuring rods laid out along the circumference
 should be Lorentz-contracted to a smaller value than at rest, by the usual factor γ. This leads to the paradox that the rigid measuring rods would have to separate from one another due to Lorentz contraction; the discrepancy noted by Ehrenfest seems to suggest that a rotated Born rigid disk should shatter.
should be Lorentz-contracted to a smaller value than at rest, by the usual factor γ. This leads to the paradox that the rigid measuring rods would have to separate from one another due to Lorentz contraction; the discrepancy noted by Ehrenfest seems to suggest that a rotated Born rigid disk should shatter.Thus Ehrenfest argued by reductio ad absurdum
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
that Born rigidity
Born rigidity
Born rigidity, proposed by and later named after Max Born, is a concept in special relativity. It is one answer to the question of what, in special relativity, corresponds to the rigid body of non-relativistic classical mechanics....
is not generally compatible with special relativity. It's worth mentioning that according to special relativity an object cannot be spun up from a non-rotating state while maintaining Born rigidity, but once it has achieved a constant nonzero angular velocity it does maintain Born rigidity without violating special relativity, and then (as Einstein later showed) a disk riding observer will measure a circumference:
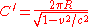 .
.Brief history
Citations to the papers mentioned below (and many which are not) can be found in a paper by Øyvind GrønØyvind Grøn
Øyvind Grøn is a Norwegian physicist.He was born in Oslo, and is a twin. He took the cand.real. degree at the University of Oslo in 1973, majoring in meteorology. He followed up with the dr.philos. degree in 1990 with a thesis on repulsive gravitation...
which is available on-line.

- 1909: Max BornMax BornMax Born was a German-born physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a number of notable physicists in the 1920s and 30s...
introduces a notion of rigid motionBorn rigidityBorn rigidity, proposed by and later named after Max Born, is a concept in special relativity. It is one answer to the question of what, in special relativity, corresponds to the rigid body of non-relativistic classical mechanics....
in special relativity. - 1909: After studying Born's notion of rigidity, Paul EhrenfestPaul EhrenfestPaul Ehrenfest was an Austrian and Dutch physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem.- Biography :Paul Ehrenfest was born and grew up in Vienna in a Jewish...
demonstrated by means of a paradox about a cylinder that goes from rest to rotation, that most motions of extended bodies cannot be Born rigid. - 1910: Gustav HerglotzGustav HerglotzGustav Herglotz was a German mathematician. He is best known for his works on the theory of relativity and seismology....
and Fritz NoetherFritz NoetherFritz Alexander Ernst Noether was a German-born mathematician.Fritz Noether's father Max Noether was a mathematician and professor in Erlangen. The notable mathematician Emmy Noether was his elder sister; the mathematician Gottfried Noether was his son.Fritz Noether was also an able mathematician...
independently elaborated on Born's model and showed, that Born rigidity only allows of three degrees of freedom for bodies in motion. That is, it's possible that a body is capable of moving in uniform translation and uniform rotation, yet accelerated rotation is impossible. So a Born rigid body cannot be brought from a state of rest into rotation, confirming Ehrenfest's result. - 1910: Max PlanckMax PlanckMax Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
calls attention to the fact that one should not confuse the problem of the contraction of a disc due to spinning it up, with that of what disk-riding observers will measure as compared to stationary observers. He suggests that resolving the first problem will require introducing some material model and employing the theory of elasticityElasticity (physics)In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
. - 1910: Theodor KaluzaTheodor KaluzaTheodor Franz Eduard Kaluza was a German mathematician and physicist known for the Kaluza-Klein theory involving field equations in five-dimensional space...
points out that there is nothing inherently paradoxical about the static and disk-riding observers obtaining different results for the circumference. This does however imply, he argues, that "the geometry of the rotating disk" is non-euclidean. He asserts without proof that this geometry is in fact essentially just the geometry of the hyperbolic planeHyperbolic geometryIn mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
. - 1911: Max von LaueMax von LaueMax Theodor Felix von Laue was a German physicist who won the Nobel Prize in Physics in 1914 for his discovery of the diffraction of X-rays by crystals...
shows, that an accelerated body has an infinite amount of degrees of freedom, thus no rigid bodies can exist in special relativity. - 1916: While writing up his new general theory of relativity, Albert EinsteinAlbert EinsteinAlbert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
notices that disk-riding observers measure a longer circumference, C′ = 2π r √(1−v2)−1. That is, because rulers moving parallel to their length axis appear shorter as measured by static observers, the disk-riding observers can fit more small rulers of a given length around the circumference than stationary observers could. - 1922: Henri BecquerelHenri BecquerelAntoine Henri Becquerel was a French physicist, Nobel laureate, and the discoverer of radioactivity along with Marie Curie and Pierre Curie, for which all three won the 1903 Nobel Prize in Physics.-Early life:...
claims that Ehrenfest was right, not Einstein. - 1935: Paul LangevinPaul LangevinPaul Langevin was a prominent French physicist who developed Langevin dynamics and the Langevin equation. He was one of the founders of the Comité de vigilance des intellectuels antifascistes, an antifascist organization created in the wake of the 6 February 1934 far right riots...
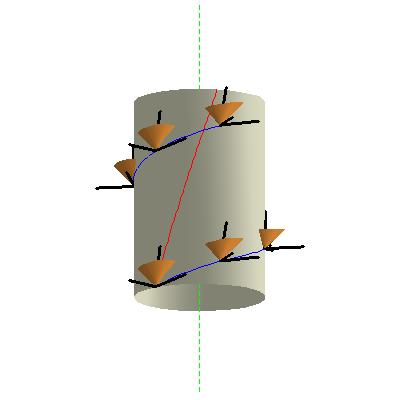
essentially introduces a moving frameMoving frameIn mathematics, a moving frame is a flexible generalization of the notion of an ordered basis of a vector space often used to study the extrinsic differential geometry of smooth manifolds embedded in a homogeneous space.-Introduction:...
(or frame fieldFrame fields in general relativityIn general relativity, a frame field is a set of four orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime...
in modern language) corresponding to the family of disk-riding observers, now called Langevin observers. (See the figure.) He also shows that distances measured by nearby Langevin observers correspond to a certain Riemannian metric, now called the Langevin-Landau-Lifschitz metric. (See Born coordinatesBorn coordinatesIn relativistic physics, the Born coordinate chart is a coordinate chart for Minkowski spacetime, the flat spacetime of special relativity. It is often used to analyze the physical experience of observers who ride on a ring or disk rigidly rotating at relativistic speeds...
for details.) - 1937: Jan Weyssenhoff (now perhaps best known for his work on Cartan connectionCartan connectionIn the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
s with zero curvature and nonzero torsion) notices that the Langevin observers are not hypersurface orthogonal. Therefore, the Langevin-Landau-Lifschitz metric is defined, not on some hyperslice of Minkowski spacetime, but on the quotient spaceQuotient spaceIn topology and related areas of mathematics, a quotient space is, intuitively speaking, the result of identifying or "gluing together" certain points of a given space. The points to be identified are specified by an equivalence relation...
obtained by replacing each world line with a point. This gives a three-dimensional smooth manifold which becomes a Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
when we add the metric structure. - 1946: Nathan RosenNathan RosenNathan Rosen was an American-Israeli physicist noted for his study on the structure of the hydrogen molecule and his work with Albert Einstein and Boris Podolsky on entangled wave functions and the EPR paradox.-Background:Nathan Rosen was born into a Jewish family in Brooklyn, New York...
shows that inertial observers instantaneously comoving with Langevin observers also measure small distances given by Langevin-Landau-Lifschitz metric. - 1946: E. L. Hill analyzes relativistic stresses in a material in which (roughly speaking) the speed of sound equals the speed of light and shows these just cancel the radial expansion due to centrifugal force (in any physically realistic material, the relativistic effects lessen but do not cancel the radial expansion). Hill explains errors in earlier analyses by Arthur EddingtonArthur Stanley EddingtonSir Arthur Stanley Eddington, OM, FRS was a British astrophysicist of the early 20th century. He was also a philosopher of science and a popularizer of science...
and others. - 1952: C. Møller attempts to study null geodesics from the point of view of rotating observers (but incorrectly tries to use slices rather than the appropriate quotient space)
- 1968: V. Cantoni provides a straightforward, purely kinematical explanation of the paradox.
- 1975: Øyvind GrønØyvind GrønØyvind Grøn is a Norwegian physicist.He was born in Oslo, and is a twin. He took the cand.real. degree at the University of Oslo in 1973, majoring in meteorology. He followed up with the dr.philos. degree in 1990 with a thesis on repulsive gravitation...
writes a classic review paper about solutions of the "paradox" - 1977: Grünbaum and Janis introduce a notion of physically realizable "non-rigidity" which can be applied to the spin-up of an initially non-rotating disk (this notion is not physically realistic for real materials from which one might make a disk, but it is useful for thought experiments).
- 1981: Grøn notices that Hooke's lawHooke's lawIn mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
is not consistent with Lorentz transformations and introduces a relativistic generalization. - 1997: T. A. Weber explicitly introduces the frame field associated with Langevin observers.
- 2000: Hrvoje Nikolić points out that the paradox disappears when (in accordance with general theory of relativity) each piece of the rotating disk is treated separately, as living in his own local non-inertial frame.
- 2002: Rizzi and Ruggiero (and Bel) explicitly introduce the quotient manifold mentioned above.
Resolution of the paradox
Grøn states that the resolution of the paradox stems from the impossibility of synchronizing clocks in a rotating reference frame.The modern resolution can be briefly summarized as follows:
- Small distances measured by disk-riding observers are described by the Langevin-Landau-Lifschitz metric, which is indeed well approximated (for small angular velocity) by the geometry of the hyperbolic plane, just as Kaluza had claimed.
- For physically reasonable materials, during the spin-up phase a real disk expands radially due to centrifugal forces; relativistic corrections partially counteract (but do not cancel) this Newtonian effect. After a steady-state rotation is achieved and the disk has been allowed to relax, the geometry "in the small" is approximately given by the Langevin-Landau-Lifschitz metric.
Common misconceptions
Surveying the somewhat dismal history sketched in the paper by Grøn (and several recent arXivArXiv
The arXiv |Chi]], χ) is an archive for electronic preprints of scientific papers in the fields of mathematics, physics, astronomy, computer science, quantitative biology, statistics, and quantitative finance which can be accessed online. In many fields of mathematics and physics, almost all...
preprints which repeat various long-corrected errors originally made by earlier authors), we can identify a number of major conceptual errors which are common to many incorrect claims which have been made over the years concerning "the geometry of a rotating disk":
- The assumption that there is a unique geometry, even a Riemannian geometryRiemannian geometryRiemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, describing a rotating disk as measured by disk-riding observers. In fact, there are several distinct but operationally significant notions of "distance" which can be employed by accelerating observers (such as the Langevin observers), even in flat spacetime. These are not even symmetricSymmetric relationIn mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
for large distances. However, for small distances they do all agree with a Riemannian metric, the Langevin-Landau-Lifschitz metric. (See Born coordinatesBorn coordinatesIn relativistic physics, the Born coordinate chart is a coordinate chart for Minkowski spacetime, the flat spacetime of special relativity. It is often used to analyze the physical experience of observers who ride on a ring or disk rigidly rotating at relativistic speeds...
for mathematical details.) - The assumption that the geometry is defined on some spatial hyperslice. In fact, it is defined on the quotient manifold obtained by collapsing the world lines of the Langevin observers to points.
- Attempts to compare the geometry of an initially non-rotating disk "before" and "after" a spin-up phase which avoid any consideration of how the material of the disk reacts to being stressed during the spin-up phase are doomed to fail, as Planck already knew in 1910.
- Ignoring the common-sense expectation that an initially non-rotating disk which is spun-up should exhibit stresses similar to those we would compute in Newtonian physics, but with relativistic corrections which should be small for a slow but steady spin-up.
- Failure to account for the fact that, because any point of the cylinder not on the axis of rotation experiences centripetal acceleration of v2/r during rotation, some general relativistic corrections are appropriate. (Here r is the perpendicular distance from the point to the axis, and v is the speed at which the point moves.)
Although the theory to resolve the paradox was understood by 1937, many subsequent authors have repeated various conceptual errors which had already been cleared up in earlier work, possibly because some of the explanations were not quite explicit.
See also
- Born coordinatesBorn coordinatesIn relativistic physics, the Born coordinate chart is a coordinate chart for Minkowski spacetime, the flat spacetime of special relativity. It is often used to analyze the physical experience of observers who ride on a ring or disk rigidly rotating at relativistic speeds...
, for a coordinate chart adapted to observers riding on a rigidly rotating disk - Length contractionLength contractionIn physics, length contraction – according to Hendrik Lorentz – is the physical phenomenon of a decrease in length detected by an observer of objects that travel at any non-zero velocity relative to that observer...
Some other "paradoxes" in special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
- Bell's spaceship paradoxBell's spaceship paradoxBell's spaceship paradox is a thought experiment in special relativity involving accelerated spaceships and strings. The results of this thought experiment are for many people paradoxical. While J. S. Bell's 1976 version of the paradox is the most widely known, it was first designed by E. Dewan and M...
- Ladder paradoxLadder paradoxThe ladder paradox is a thought experiment in special relativity. It involves a ladder travelling horizontally and undergoing a length contraction, the result of which being that it can fit into a much smaller garage...
- Physical paradoxPhysical paradoxA physical paradox is an apparent contradiction in physical descriptions of the universe. While many physical paradoxes have accepted resolutions, others defy resolution and may indicate flaws in theory...
- Supplee's paradoxSupplee's paradoxIn relativistic physics, Supplee's paradox arises when considering the buoyant force exerted on a relativistic bullet immersed in a fluid subject to an ambient gravitational field...
- Twin paradoxTwin paradoxIn physics, the twin paradox is a thought experiment in special relativity, in which a twin makes a journey into space in a high-speed rocket and returns home to find he has aged less than his identical twin who stayed on Earth...
External links
- The Rigid Rotating Disk in Relativity, by Michael Weiss (1995), from the sci.physics FAQ.
- Einstein's Carousel (section 3.4.4), by B. Crowell

